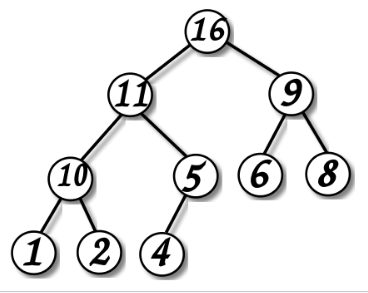
16 → 11 →10 → 1, 2; 5 → 4; 9 → 6, 8
ƒерево — это абстрактна€ структура данных, иерархи€ которой похожа на дерево. —остоит из св€занных узлов, один из которых €вл€етс€ «корнем». аждый узел может иметь одного предка и/или одного или нескольких потомков. (ƒерево €вл€етс€ св€зным графом без циклов.)
орень дерева — это самый верхний узел.
ƒерево можно определить рекурсивно как множество узлов, один из которых €вл€етс€ корнем, при этом каждый узел €вл€етс€ структурой данных, содержащей некое значение, а также ссылки на другие (дочерние ему) узлы, при условии, что на корневой узел ссылки нет, а на остальные узлы имеетс€ ровно по одной ссылке.
Ћист — узел, не имеющий дочерних элементов (потомков).
¬нутренний узел — узел дерева, имеющий потомков.
√лубина дерева — самый длинный путь от корн€ дерева до его листа.
ƒерево, в котором каждый узел имеет не более двух потомков, называетс€ двоичным деревом.

16
→ 11 →10 → 1, 2; 5 → 4; 9 → 6, 8
ќбход дерева «в глубину»: обход всех потомков каждого узла. ”добно реализовывать рекурсивно:
ѕроцедура ќбход дерева в глубину
ќбход поддерева в глубину <вх: дерево.root>
онец процедуры
ѕроцедура ќбход поддерева в глубину <вх: node: узел дерева>
ќбработать узел<вх: node>
÷икл дл€ каждого узла child из node.childs выполн€ть
ќбход поддерева в глубину <вх: child>
онец цикла
онец процедуры

16
→ 11 → 9 → 10 → 5 → 6 → 8 → 1 →
2 → 4
ќбход дерева «в ширину»: обход последовательно узлов одного уровн€, переход€ последовательно от верхних уровней к нижним. ѕор€док посещени€ узлов удобно организовать при помощи очереди
ѕроцедура ќбход дерева в ширину
ќчередь_узлов.сделать пустой
ќчередь_узлов.добавить<вх: дерево.root>
÷икл пока ќчередь_узлов.непуста выполн€ть
ќчередь_узлов.вз€ть элемент из очереди в <вых: node>
ќбработать узел<вх: node>
÷икл дл€ каждого узла child из node.childs выполн€ть
ќчередь_узлов.добавить элемент в конец очереди <вх: child>
онец цикла
онец цикла
онец процедуры
ƒвоична€ куча (пирамида, сортирующее дерево) — это двоичное дерево, удовлетвор€ющее следующим услови€м:
1) «начение в каждом узле дерева не меньше, чем значение в любом из потомков этого узла;
2) аждый лист имеет глубину d или d-1, где d – глубина дерева;
3) —амый глубокий слой заполн€етс€ без пропусков.
«начени€, содержащиес€ в узлах двоичной кучи, удобно хранить в массиве послойно, начина€ сверху дерева. орень дерева хранитс€ в Array[0], его левый потомок в Array[1], правый в Array[2] и т. д. ѕотомки элемента Array[i] наход€тс€ в Array[2*i+1] и Array[2*i+2].
ѕри нумерации с нул€ слоев дерева сверху вниз и узлов сло€ слева направо, i-й узел в j-м слое хранитс€ в элементе вектора с индексом i+2j-1 (при индексации элементов вектора, начина€ с 0).
ѕример 1. —ледующий массив хранит содержимое приведенной на рисунке двоичной кучи:
|
16 |
11 |
9 |
10 |
5 |
6 |
8 |
1 |
2 |
4 |

¬опрос. ак по индексу в массиве вычислить дл€ элемента номер уровн€ в дереве и его номер в уровне?
N → L, n
3(10) → 2,
L = [log2(N + 1)], n = N – (2L - 1)
»ндекс 9 (элемент 4) → L=3, n = 2
¬опрос. ак по номеру уровн€ в дереве и его номеру в уровне вычислить индекс в массиве ?
L, n → N = 2L – 1 + n
Ёлемент 4: L=3, n=2 => N = 9
¬опрос. ак массив превратить в двоичную кучу?
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
4 |
10 |
-7 |
3 |
12 |
16 |
-10 |
4 |
5 |
1 |
-2 |
0 |
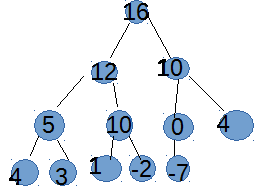
Ћюбой массив можно представить в виде двоичного дерева, удовлетвор€ющего свойствам 2) и 3). ќстаетс€ только переместить значени€ элементов внутри массива так, чтобы они удовлетвор€ли свойству 1).
Ѕудем использовать итеративный метод, ид€ снизу дерева вверх, проход€ по всем внутренним узлам (то есть узлам, не €вл€ющимис€ листь€ми) справа налево, превраща€ каждое дерево с корнем в текущем узле в двоичную кучу.
ѕри таком пор€дке обхода у каждого текущего узла оба поддерева будут уже обойдены, то есть превращены в двоичную кучу. Ќам остаетс€ только объединить их с текущим узлом так, чтобы результат был тоже двоичной кучей.
—ледующа€ процедура (heapify) реализует описанный алгоритм:
ѕроцедура heapify<вх: ar: массив, N: целое число>
! ƒано: массив ar, N – размер массива
! Ќадо: массив ar содержит двоичную кучу размера N
! јлгоритм: превращаем «хвост» массива в двоичную кучу,
! последовательно сдвига€ начало «хвоста» к началу массива
start := parent(N-1) ! start := индекс самого последнего внутреннего узла
÷икл пока start >= 0 выполн€ть
siftDown(ar, start, N-1) ! ѕросе€ть: если надо, переместить содержимое
! корн€ вниз, чтобы дерево стало двоичной кучей
start = start – 1 ! ѕереходим к предыдущему внутреннему узлу
онец цикла
онец процедуры
ѕроцедура parent<вх: n: индекс узла в массиве>
! ¬озвращает индекс родительского узла
ответ := (n – 1) / 2
онец процедуры
ѕроцедура siftDown основываетс€ на том, что оба дочерних поддерева некоего узла уже €вл€ютс€ двоичными кучами, и теперь надо все дерево с корнем в этом узле сделать двоичной кучей. ≈сли значение V в рассматриваемом узле больше значений в обоих его дочерних узлах — все в пор€дке, по определению дерево уже €вл€етс€ двоичной кучей.
¬ противном случае нам придетс€ переместить V вниз по дереву. ѕеремещение происходит посредством обмена значени€ми двух узлов — родительского и дочернего (того из дочерних, в котором бќльшее значение): большее значение идет вверх, меньшее вниз. ѕроцесс напоминает сортировку «пузырьком», только здесь «пузырек» проходит не по всему массиву, а только по одной ветви дерева, что существенно сокращает его путь: c O(N) до O(log N).
»так, если V оказалось меньше, чем значение в дочернем узле, мы обмениваем значение V с наибольшим из значений, наход€щихс€ в двух его дочерних узлах. Ёту же процедуру проводим снова с тем узлом, куда переместилось V и так далее.
ѕроцедура siftDown<вх: ar: массив, root: индекс, end: индекс>
! ѕочинить кучу, корень которой находитс€ в элементе с индексом root,
! предполага€, что оба дочерних поддерева €вл€ютс€ двоичными кучами
! end – индекс последнего узла дерева
! ѕока у корн€ есть дочерний узел со значением большим, чем значение в корне
÷икл пока ((leftChild(root) <= end) и (ar[root] < ar[leftChild(root))) или
((rightChild(root) <= end) и (ar[root] < ar[rightChild(root)))) выполн€ть
! ≈сли значение в левом дочернем узле больше, чем в правом
≈сли (rightChild(root) > end) или (ar[leftChild(root)] > ar[rightChild(root)]) то
swap(root, leftChild(root)) ! ќбмениваем значени€ корн€ и левого дочернего узла
root := leftChild(root)
»наче
swap(root, rightChild(root)) ! ќбмениваем значени€ корн€ и правого дочернего узла
root := rightChild(root)
онец если
онец цикла
онец процедуры
ѕроцедура leftChild<вх: n: индекс узла в массиве>
! ¬озвращает индекс левого дочернего узла
ответ := n * 2 + 1
онец процедуры
ѕроцедура rightChild<вх: n: индекс узла в массиве>
! ¬озвращает индекс правого дочернего узла
ответ := n * 2 + 2
онец процедуры