Лекция 15

Добавление элементов к двоичной куче

Двоичная куча (пирамида, сортирующее дерево) — это двоичное дерево, удовлетворяющее следующим условиям:

1) Значение в каждом узле дерева не меньше, чем значение в любом из потомков этого узла;

2) Каждый лист имеет глубину d или d-1, где d – глубина дерева;

3) Самый глубокий слой заполняется без пропусков.

При добавлении элемента в конец массива тот может перестать быть двоичной кучей (о двоичных кучах см. предыдущую лекцию). Для восстановления свойства 1 двоичной кучи (значение в узле больше значения в любом из его потомков) может потребоваться переместить этот элемент вверх по дереву. Для этого значение в добавленном узле сравнивается со значением в родительском узле и, в случае нарушения порядка (то есть если оно больше, чем значение в родительском узле) обменивается со значением в родительском узле. Это действие производится до тех пор, пока добавленное значение не поднимется вверх настолько, что значение в родительском узле окажется больше него, или пока не достигнет корня дерева.

Процедура добавить элемент в двоичную кучу <вх: куча, E: элемент>

куча.массив[куча.размер] := E

siftUp<вх: куча.массив, куча.размер>

куча.размер := куча.размер + 1

Конец процедуры

Процедура siftUp<вх: ar: массив, n: индекс элемента>

! Поднимает элемент с индексом n вверх по дереву, пока значение

! не окажется меньше, чем в родительском узле (или не достигнет корня)

Цикл пока parent(n) >= 0 и ar[n] > ar[parent(n)] выполнять

swap(ar, n, parent(n))

n := parent(n)

Конец цикла

Конец процедуры

Сортировка HeapSort

Двоичная куча может быть использована для сортировки массива без использования дополнительного места (in place). Этот метод очень похож на метод сортировки «пузырьком», но максимальный путь, который проходит «пузырек», имеет длину не O(N), а O(log N).

Сначала массив превращается в двоичную кучу (сложность алгоритма O(N)), затем, пока куча не станет пустой, из нее удаляется максимальный элемент: содержимое корня кучи (то есть максимальный элемент) меняется с содержимым последнего элемента дерева, размер дерева уменьшается на 1 и получившееся дерево снова превращается в двоичную кучу. Сложность последнего действия O(log N), применение его ко всем элементам массива дает O(N log N).

Так как максимальный элемент кучи при удалении всегда помещается в ячейку сразу за кучей, то в массиве будут находится двоичная куча и сразу после нее отсортированные по возрастанию элементы. После того, как куча станет пустой, весь массив будет занят элементами, отсортированными по возрастанию.

Этот метод сортировки называется HeapSort (пирамидальная сортировка, сортировка кучей).

Процедура HeapSort<вх: аr: массив, N: целое числа>

! Дано: массив ar неотсортирован, N – размер массива ar

! Надо: массив ar отсортирован

heapify(ar, N) ! Окучить: преобразовать массив в двоичную кучу

Цикл пока N > 0 выполнять

N := N -1 ! Уменьшить размер кучи

swap(ar[N], ar[0]); ! Обменять

siftDown(ar, 0, N); ! Просеять: переместить содержимое корня вниз,

! пока дерево снова не станет двоичной кучей

Конец цикла

Конец процедуры

Очередь с приоритетами (priority queue).

Очередь — FIFO (стек - LIFO)

Очередь с приоритетами — это структура данных очередь, элементы которой упорядочены по приоритету.

При добавлении элемента он добавляется в очередь перед теми элементами, у которых приоритет ниже, чем у него.

Очередь с приоритетами удобно реализовывать на основе двоичной кучи. Головой очередь будет корень двоичного дерева. При удалении элемента (корня) из очереди с приоритетами двоичная куча перестраивается для сохранения своего свойства (значение в узле больше, чем значения во всех его потомках).

Применение priority queue в алгоритме Дейкстры нахождения кратчайшего пути в графе.

Граф — это структура данных, состоящая из набора вершин и набора ребер, которые могут связывать пару вершин.

Ребра могут быть однонаправленные или двунаправленные.

Ребра могут иметь вес (нагрузку), который иногда называется длиной ребра. В этом случае граф называется нагруженным.

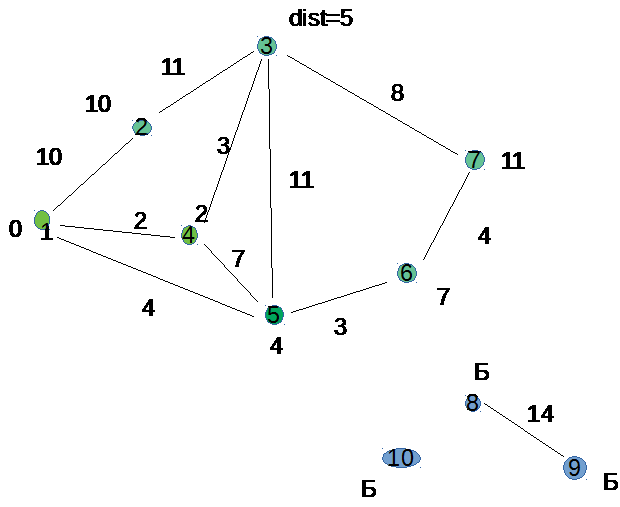
Алгоритм Дейкстры находит кратчайший путь между двумя вершинами в нагруженном графе с положительными длинами ребер.

Пример использования

Задача latchup (защелка) → граф → для всех вершин графа проверялось, что есть путь не длиннее, чем R (минимальное расстояние до заземления).

Задача поиска кратчайшего пути в многоугольнике с препятствиями (the shortest way in polygon with obstacles).

(Когда задача не имеет точного решения (в виде формулы) — приближенное решение или симуляция (моделирование)).

Описание алгоритма Дейкстры

Назовем расстоянием узла Y расстояние от начального узла до узла Y. Будем хранить его в dist[Y].

1. Присваиваем каждому узлу бесконечное расстояние.

2. Возьмем в качестве текущего узла начальный узел. Все остальные узлы пометим как «непосещенные».

3. Для текущего узла рассмотрим всех соседей (соединенных с ним ребром). Вычислим для каждого из соседей пробную длину - длину пути через текущий узел (dist текущего узла + вес ребра, соединяющего текущий узел и соседа) и, если она меньше dist соседа, заменим dist этого соседа на эту пробную длину.

4. Помечаем текущий узел как «посещенный», удаляем из множества непосещенных узлов и больше не рассматриваем.

5. Если узел назначения оказывается помеченным как «посещенный» или если нет пути ко всем непосещенным узлам, алгоритм заканчивает работу.

6. Если же есть непосещённые узлы с dist меньше, чем бесконечность, среди них выбирается узел с наименьшим dist, берется в качестве текущего и алгоритм переходит к шагу 3.

Использование бинарной кучи в реализации алгоритма Дейкстры

Сначала добавим в кучу исходный узел.

Затем последовательно извлекаем из кучи элемент с наименьшим значением и рассматриваем его как текущий. Заметим, что на первом шаге текущим будет сам исходный узел.

Для каждого рассматриваемого текущего узла вычисляем длину пути (из исходной вершины), проходящего через него, ко всем его соседям. Эта длина равна сумме значения в текущем узле и весу ребра, соединяющего текущую и соседнюю вершины.

Если для какого-то соседнего узла вновь вычисленная длина пути оказывается меньше, чем известная ранее (то есть хранящаяся в узле), то меняем значение dist для этого соседнего узла. Если соседнего узла еще нет в куче, то добавляем его туда. Если же он уже содержится в куче, то переформируем кучу из-за изменения значения в узле.

Процедура Дейкстра<вх: graph: граф, source: исходный узел>

dist[source] := 0

двоичная_куча.сделать пустой

Цикл для каждой вершины v графа graph выполнять

Если v не равна source то

dist[v] := INFINITY

предыдущая[v] := UNDEFINED

Конец если

Конец цикла

двоичная_куча.добавить<вх: source, 0>

Цикл пока двоичная_куча.не пуста выполнять

двоичная_куча.извлечь минимальный<вых: u>

Цикл для каждого соседа v вершины u выполнять

alt := dist[u] + length(u, v)

Если alt < dist[v] то

dist[v] := alt

предыдущий[v] := u

Если двоичная_куча.содержит<вх: v> то

двоичная_куча.уменьшить приоритет(v, alt)

Иначе

двоичная_куча.добавить<вх: v>

Конец если

Конец цикла

Конец процедуры