”тверждение.
a) ƒл€ каждого посещенного узла v dist[v] €вл€етс€ наименьшей длиной пути от исходной вершины source до узла v.
b) ƒл€ каждого непосещенного узла u dist[u] €вл€етс€ наименьшей длиной пути от source до u.
ƒоказательство по индукции по числу посещенных узлов.
1) Ѕаза: если посещен только один узел (source), dist дл€ всех непосещенных узлов равна длине ребра, идущего в них из source, если такое ребро существует, и бесконечности, если такого ребра нет. ¬ этом случае
- верность предположени€ a) очевидна (путь от source до source равен 0 и это кратчайший путь). - предположение b) также верно, так как кратчайший путь из source в каждую непосещенную вершину как раз и будет ребро, св€зывающее source и эту вершину, если это ребро существует. ¬ противном случае длина кратчайшего пути бесконечность, то есть тоже равна dist.
2) ƒопустим, предположение верно дл€ n-1 узлов. ѕо алгоритму ƒейкстры n-ым посещенным узлом будет узел u, такой, что значение dist[u] – наименьшее из всех непосещенных узлов. ƒокажем, что dist[u] – длина кратчайшего пути от source до u.
Ѕудем доказывать от обратного.
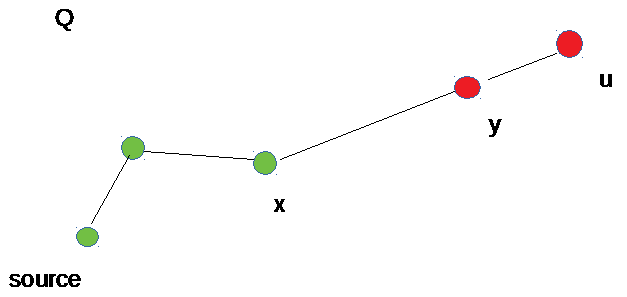
ѕусть существует более короткий путь Q от source до u: len(Q) < dist[u]. (1)
ѕусть y – перва€ непосещенна€ вершина на этом пути (возможно, это u) и x – вершина непосредственно перед y на этом пути.

“огда len(Qx) + len(x,y) <= len(Q) (2), где Qx – часть пути Q от source до x, а len(x,y) – длина ребра между x и y.
“ак как по предположению индукции dist[x] – длина кратчайшего пути от source до x, то dist[x] <= len(Qx) (3).
“ак как y – смежна€ с x (т.е. соединена ребром), то значение dist[y] должен быть настроено алгоритмом: dist[y] <= dist[x] + len(x,y) (4).
“ак как из всех непосещенных вершин алгоритм выбрал u (вершина с наименьшим значением dist из непосещенных), то dist[u] <= dist[y] (5).
“аким образом, мы имеем следующую цепочку неравенств:
(3) (2) (1) (5) (4)
dist[x] + len(x,y) <= len(Qx) + len(x,y) <= len(Q) < dist[u] <= dist[y] <= dist[x] + len(x,y)
из которой следует, что:
dist[x] < dist[x],
что означает, что мы пришли к противоречию.
«адача. ѕревратить бинарное берево поиска в упор€доченный L1-список (пройти по бинарному дереву поиска в пор€дке возрастани€ значений)
—ѕ L1-списка
5. ѕоставить указатель в начало списка === указатель := Ќайти минимальный элемент в поддереве
6. ѕередвинуть указатель вперед === указатель := —ледующий узел <вх: указатель>
7. Ёлемент за указателем === указатель.«начение элемента
8. ¬ставить элемент за указателем === ??? дл€ упор€доченного L1-списка — не имеет смысла
9. ”далить элемент за указателем === ???
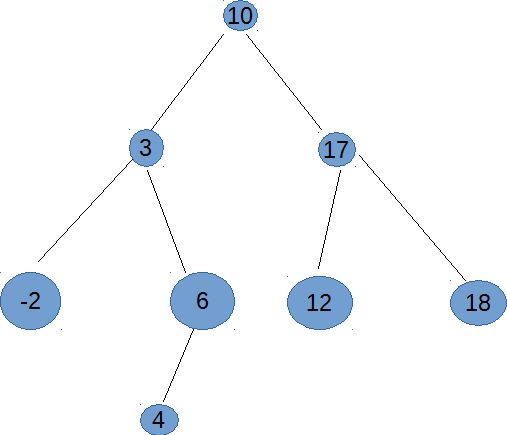
Ѕинарное дерево поиска — такое бинарное дерево, в котором значение в узле больше, чем значени€ в его левом поддереве и меньше, чем значение в его правом поддереве.
¬ каждом узле хранитс€ ссылка на левый и правый дочерний узлы, а также ссылка на родительский узел. ѕри отсутствии у узла правого или левого дочернего узла ссылки на них вырождены (равны 0).
ѕоиск.
ѕроцедура Ќайти значение<вх: V>
текущий узел := дерево.корень
цикл пока текущий узел не вырожден
если текущий узел.значение == V то
ответ := текущий узел
найдено := да
выйти из процедуры
иначе
если текущий узел.значение > V то
текущий узел := текущий узел.левый дочерний узел
иначе
текущий узел := текущий узел.правый дочерний узел
конец если
конец если
конец цикла
ответ := текущий узел.родительский узел.значение
найдено := нет
онец процедуры
ƒобавление.
ѕроцедура ƒобавить элемент к дереву <вх: V: элемент, U: узел>
! ƒобавл€ем элемент V как дочерний узел узла U
дерево.создать новый узел<вых: новый узел>
новый узел.левый дочерний узел := 0
новый узел.правый дочерний узел := 0
если U.значение > V то
U.левый дочерний узел := новый узел
иначе
U.правый дочерний узел := новый узел
конец если
онец процедуры
ѕоиск минимального
ѕроцедура Ќайти минимальный элемент в поддереве <вх: U: узел>
! Ќаходим минимальный элемент поддерева с корнем в U
текущий узел = U
цикл пока (текущий узел != 0) и (текущий узел.левый дочерний узел != 0)
текущий узел := текущий узел.левый дочерний узел
конец цикла
ответ := текущий узел
онец процедуры
ѕоиск максимального — аналогично
ѕроход по дереву в пор€дке возрастани€ значений
ѕроцедура —ледующий узел<вх: узел>
если узел.правый дочерний узел != 0 то
ответ := найти минимальный элемент<вх: узел> (1)
иначе
если узел == узел.родительский узел.левый дочерний узел то
ответ := узел.родительский узел (2)
иначе
цикл пока узел == узел.родительский узел.правый дочерний узел выполн€ть
узел := узел.родительский узел
конец цикла
утверждение: узел — левый дочерний узел своего родительского узла
ответ := узел.родительский узел (3)
конец если
конец если
онец процедуры
(2) (1) (2) (3) (1) (2) (1)
-2 → 3 → 4 → 6 → 10 → 12 → 17 → 18