-
Является ли кучей следующий массив:
int a[] = {20, 18, 10, 15, 7, 7, 9, 8, 10, 6, 4, 5}?
-
Рассматривается реализация максимальной бинарной кучи на базе
динамического массива.
Пусть первоначально в куче содержатся следующие 10 элементов
в указанном порядке:
10, 9, 8, 7, 6, 5, 4, 3, 2, 1.
Из кучи трижды удаляется максимальный элемент,
при этом каждый раз структура кучи восстанавливается.
В каком порядке после этого будут содержаться в массиве
оставшиеся 7 элементов?
-
Предположим, что в двоичном дереве поиска
хранятся целые числа и мы хотим найти
число 363. Может ли следующая последовательность
быть последовательностью просматриваемых при этом
ключей:
1001, 180, 820, 201, 835, 245, 363?
-
Нарисуйте двоичные деревья поиска высоты
3, 4, 5 и 6 для одного и того же множества
элементов:
{1, 3, 4, 9, 16, 17, 20}.
-
В дерево поиска последовательно добавляются
числа от 1 до 15. В каком порядке их следует
добавлять, чтобы дерево имело
а) минимально возможную высоту?
б) максимально возможную высоту?
-
Предположим, что в двоичном дереве поиска
хранятся целые числа и мы хотим найти
число 363. Может ли следующая последовательность
быть последовательностью просматриваемых при этом
ключей:
925, 202, 920, 240, 912, 245, 363?
-
Пусть вершина x двоичного дерева поиска имеет
двоих детей. Сколько детей в этом дереве поиска
может иметь следующая по величине вершина?
-
Приведите обратную польскую запись для
выражения
7 - (5 * 3) / ((9 -100) * (2 / (77 + 15)).
-
В изначально пустое дерево поиска, содержащее
в вершинах целые значения, последовательно
добавляются элементы:
1, 10, 2, 5, 6, 4, 3, 9.
Какое дерево получится в результате?
-
В дереве поиска с отмеченной вершиной
(рисунок прилагается) указать вершины, содержащие
следующее и предыдущее по порядку значения.
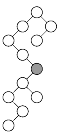
-
В дереве поиска с отмеченной вершиной
(рисунок прилагается) указать вершины, содержащие
минимальное и максимальное значения в поддереве с
корнем в отмеченной вершине.
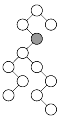
-
Является ли данное дерево,
вершины которого раскрашены в красный и черный цвета
(рисунок прилагается), красно-черным?
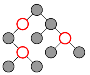
-
Всякое ли красно-черное дерево является
AVL-деревом?
-
Верно ли, что вершины произвольного AVL-дерева можно
раскрасить в черные и красные цвета так, чтобы получилось
красно-черное дерево?
-
Существует ли красно-черное дерево высоты 6,
содержащее 13 вершин?
-
Какое минимальное количество вершин может быть в красно-черном
дереве высоты 5?
-
В изначально пустое красно-черное дерево,
вершины которого содержат целочисленные
значения, последовательно добавляются значения
5, 4, 2, 3, 0, 1. Указать, как модифицируется
дерево на каждом шаге после добавления и
ребалансировки.
-
Подсчитайте, чему равно 350(mod 20).
-
Применив алгоритм быстрого возведения в степень,
вычислить без использования компьютера, чему
равно 360(mod 11).
-
Найти такие целые u и v, что
121u + 59v = 1.
-
По аналогии с алгоритмом быстрого возведения
в степень, составить алгоритм быстрого вычисления
произведения двух целых чисел, использующий лишь
операции сложения, вычитания, удвоения и деления
пополам. Пусть надо вычислить произведение чисел
a и n. В качестве инварианта цикла использовать
условие
b k + p = a n = const,
где b, k, p — целочисленные переменные,
которые меняются в теле цикла.
-
Воспользовавшись схемой инварианта цикла,
написать бинарный алгоритм деления
целых неотрицательных чисел с остатком,
который использует только операции сложения, вычитания,
удвоения и деления пополам. Даны целые неотрицательные
числа a, b≠0, получить частное от деления
q и остаток r. Использовать следующий инвариант
цикла:
a = q*b + r,
m = e*b,
e = 2k, k ≥ 0.
Условие завершения цикла: r < b.
Первоначально q=0, r=a,
e=1, m=b.
Если 2*m < r, то m и e удваиваются;
если m > r, то m и e делятся пополам. Если
то из r вычитается m, а к q прибавляется e.
-
Написать алгоритм нахождения наибольшего общего
делителя двух целых неотрицательных
чисел m и n, одновременно
не равных нулю, с использований операций
вычитания, удвоения, деления пополам и проверки
четности, работающий быстро (за время, полиномиально
зависящее от количества цифр в записи исходных чисел).
Требуется применить схему построения цикла с помощью
инварианта. В качестве инварианта использовать равенство
НОД(m, n) = с НОД(a, b),
где c — степень двойки.
Здесь m, n — исходные числа, а целочисленные
переменные a, b, с меняются в процессе
выполнения цикла так, что инвариант сохраняется.
(Основная идея: если одно из двух чисел четное, а другое
нечетное, то при делении первого на 2 наибольший общий делитель
не меняется; если оба числа нечетные, то из большего можно
вычесть меньшее; если оба четные, то их НОД равен удвоенному
НОД пары, получающейся после деления обоих чисел на 2.)
-
Для класса комплексных чисел Complex написать
прототипы методов "operator*" и "operator/=".
-
Для класса квадратных матриц Matrix написать
прототип оператора присваивания и оператора
перемножения двух матриц "operator*".
-
Для класса Complex написать прототипы методов
для оператора унарный минус и оператора "не равно"
"operator!=".
-
Ниже приведен фрагмент описания класса для
работы с комплексными числами:
class Complex
{
private:
double re, im;
...
};
Реализуйте префиксный и постфиксный операторы ++, увеличивающие
значение комплексного числа на 1.
-
Какие из вызовов 1, 2, 3, 4, 5, 6 являются корректными?
class C
{
public:
void first();
void second() const;
};
int main()
{
C c1, *p1;
const C c2, *p2;
c1.first(); // 1
p1.second(); // 2
c2.first(); // 3
p2->second(); // 4
p1->first(); // 5
p2->first(); // 6
return 0;
}
-
Ниже приведён фрагмент описания класса для
хранения перестановок:
class Permutation
{
private:
int *a; //перестановка чисел от 0 до n - 1
int n;
...
};
Напишите реализацию конструктора копирования и
оператора копирования для класса Permutation.
-
Сколько раз и где будет вызываться
конструктор копирования класса Matrix?
double det(Matrix m)
{
...
}
int main()
{
Matrix m1;
m1.read();
Matrix m2 = m1;
cout << det(m2) << endl;
return 0;
}
-
Что напечатает программа?
#include <iostream>
using namespace std;
struct Num
{
int value;
Num operator ++(int)
{
Num copy(*this);
++value;
return copy;
}
Num operator ++()
{
++value;
return *this;
}
};
int main()
{
Num a;
a.value = 1;
++(a++++);
cout << a.value << endl;
return 0;
}
-
Ниже приведен фрагмент описания класса для
хранения массива целых чисел:
class Array
{
private:
int *a;
int n;
public:
...
}
Напишите реализацию метода read(), считывающего
массив с клавиатуры. Массив задаётся в формате:
n a[0] a[1] ... a[n-1].
Память под массив выделяется динамически. Пример
использования:
Array arr1;
arr1.read();
Array arr2 = arr1;
arr2.read();
arr2.print();
-
Рассмотрим следующую программу:
#include <iostream>
using namespace std;
class A {
public:
virtual void f() {
cout << 0 << endl;
}
};
class B: public A {
public:
void f() {
cout << 1 << endl;
}
};
int main() {
...
return 0;
}
Допишите тело функции main так, чтобы получившаяся
программа печатала 1, но, если стереть слово "virtual"
в определении метода f класса A, то она печатала бы 0.
-
Какое число напечатает в 32-разрядной архитектуре
программа
#include <iostream>
using namespace std;
class A {
char s[16];
public:
virtual void f() {}
};
int main() {
A x;
cout << sizeof(x) << endl;
return 0;
}


