Практикум по алгебре
Мехмат, 3-й курс
Осенний семестр 2025-26 учебного года
Журнал группы 302, 2025-26 уч. год
Решения задач присылайте на почту по адресу
vladimir_borisen < собака > mail.ru
В теме письма обязательно указывайте номер группы 302.
Цель курса
Основной целью курса будет знакомство с системой компьютерной алгебры (или, шире, компьютерной математики) SageMath. Из ныне существующих программых пакетов компьютерной математики (Volfram Mathematika, Maple, MATLAb, Maxima и др.) SageMath является лучшим, причем особенно популярен он среди алгебраистов. Достоинствами SageMath являются то, что 1) это свободное и бесплатное программное обеспечение, которое развивается всем миром и включает в себя большинство других существующих свободных математических пакетов; 2) Sage использует язык программирования Python — тем, кто знает Python, не нужно учить дополнительно еще один язык программирования.
Поскольку SageMath является надстройкой над языком Python, мы сначала освоим Python. Знание Python'а само по себе ценно, этот язык в последние годы стал очень популярным — например, почти все программы, работающие с нейросетями, пишутся на Python'е.
В курсе будет несколько тем, по каждой нужно будет сделать одну задачу. Номер задачи по каждой теме выбирается в соответствии с номером студента в журнале. Пусть в списке задач по данной теме N задач, тогда студент должен выбрать задачу k, номер которой совпадает по модулю N с номером студента по журналу m:
Журнал группы 302, 2024-25 уч. год
Видеозаписи лекций
Видео лекции 25 сентября 2021: приложения теории чисел в криптографии. Схема RSA кодирования с открытым ключом и задачи, возникающие в связи с ней.
Видео лекции 9 октября 2021: Алгоритмы теории чисел, связанные со схемой RSA кодирования с открытым ключом — тест простоты Ферма, кармайкловы числа, вероятностный тест простоты Миллера-Рабина, ρ-алгоритм факторизации Полларда.
Видео лекции 6 ноября 2021: Классы в языке Python3.
Видео лекции 20 ноября 2021: Введение в SageMath. Геометрические задачи на нахождение замечательных точек треугольника.
Видео лекции 18 декабря 2021:
Системы алгебраических уравнений и решение различных задач, связанных
с ними, в SageMath. Коммутативные алгебры над полем как фактор-алгебры
алгебры многочленов от нескольких переменных. Идеалы в алгебре многочленов
и аффинные алгебраические многообразия.
Теорема Гильберта о конечности базисов.
Замечательная теорема Гильберта о нулях,
связь между аффинными многообразиями и радикалами идеалов.
Базисы Грëбнера
идеалов и решение с их помощью различных алгоритмических задач
в SageMath.
См. также видео лекции прошлого года
на ту же тему.
Записи лекций 2021 ("виртуальная доска")
Видео-материалы прошлых лет
Видео лекции 8 сентября 2020: обзор курса, введение в язык Python, задачи по теме "Теория чисел в криптографии".
Видео лекции 22 сентября 2020: классы в Python'е.
Видео лекции 6 октября 2020: введение в SageMath, графика в sage, задачи на замечательные точки треугольника.
Видео лекции 20 октября 2020: построение кубического сплайна средствами SageMath. Вариант C1-сплайна.
Видео лекции 3 ноября 2020: коммутативная алгебра и базисы Гребнера в SageMath. Решение различных задач, связанных с системами алгебраических уравнений.
Тема 1. Язык программирования Python
1.1. Знакомство с языком Python3
Python — простой и изящный объектно ориентированный язык. Переменные в нем не имеют типов, они содержат ссылки на объекты, а тип выражения определяется объектом, который получается в результате вычисления выражения. Это так называемая динамическая типизация — тип выражения определяется лишь во время работы программы, по тексту (статически) его не всегда возможно определить.
Python-программа не требует компиляции и сборки (вернее, эти этапы выполняются незаметно для пользователя). Интерпретатор Python'а позволяет использовать язык в качестве очень удобного калькулятора.
Python легко учится, человек, знакомый с другими алгоритмическими языками, может начать писать программы на Python'е после минимального знакомства с правилами языка, практически сразу.
В качестве примера рассмотрим программу разложения числа на простые множители. На вход функции factor(m) дается натуральное число m, на выходе мы получаем список пар. Первый элемент пары — это простой множитель, входящий в разложение m, второй — показатель степени, в которой этот множитель входит в разложение.
def factor(m):
res = []
d = 2
while m > 1 and d <= m:
if m%d == 0:
e = 0
while m%d == 0:
m //= d
e += 1
res.append((d, e))
d += 1
return res
Отметим, что квадратные скобки в Python'е обозначают список, а круглые — кортеж (tuple). Список в Python'е на самом деле представляет собой динамический массив, tuple отличается от списка тем, что его элементы нельзя изменять. Операция целочисленного деления обозначается двумя наклонными чертами "//", одна черта "/" обозначает обычное деление, в результате которого получается не целое, а вещественное число.
Пусть функция factor записана в файл "fact.py". Для ее выполнения запустим интерпретатор Python'а:>python3 Python 3.6.6 (default, Sep 12 2018, 18:26:19) [GCC 8.0.1 20180414 (experimental) [trunk revision 259383]] on linux Type "help", "copyright", "credits" or "license" for more information. >>>Интерпретатор выдает приглашение на ввод команды ">>>". Импортируем все функции модуля "fact" из файла "fact.py":
>>> from fact import *И затем разложим на множители несколько чисел, вызывая функцию factor:
>>> factor(100) [(2, 2), (5, 2)] >>> factor(123) [(3, 1), (41, 1)] >>> factor(561) [(3, 1), (11, 1), (17, 1)] >>> factor(1024) [(2, 10)] >>> factor(101) [(101, 1)] >>> factor(2**32 + 1) [(641, 1), (6700417, 1)]Отметим, что последнее число 232 + 1 = 4294967297 — это пятое число Ферма
1.2. Элементы теории чисел
Кодирование с открытым ключом и элементы теории чиселСодержание лекции
- Кольцо вычетов по модулю m
- Малая теорема Ферма, китайская теорема об остатках, теорема Эйлера
- Основные алгоритмы теории чисел:
- Тест простоты Ферма и кармайкловы числа
- Вероятностный тест простоты Миллера-Рабина
- Кодирование с открытым ключом, схема RSA
- Алгоритмы факторизации (разложения числа на множители):
Презентация: теория чисел в криптографии
Список задач
- Реализовать вероятностный тест простоты Миллера-Рабина.
- Реализовать алгоритм для Китайской теоремы об остатках.
- Факторизовать целое число с помощью ρ-алгоритма Полларда.
- Факторизовать целое число с помощью p-1-алгоритма Полларда (используйте упрощенный p-1 алгоритм Полларда, не требующий вычисления всех простых степеней, не превосходящих верхней границы: qiα ≤ N, вместо этого используется N!).
- Вычислить квадратный корень из x в поле Zp (p — простое число), т.е. найти r такое, что r2 ≡ x (mod p).
- * Факторизовать целое число с помощью алгоритма Ленстра на эллиптических кривых.
Нужно сделать одну задачу из списка. Всего в списке 5 задач (6-я — необязательная). Студент выбирает ту задачу, которая совпадает по модулю 5 с его номером по журналу. Например, если номер по журналу 18, выбирается задача 3, если 10 — задача 5. Вместо любой задачи можно по желанию сделать задачу 6, более сложную, чем остальные.
1.3. Классы в языке Python
Презентация:
Классы в Python'е
на примере классов R2Vector и R2Point для поддержки графики
на плоскости R2.
Оба класса содержатся в модуле R2Graph,
файл "R2Graph.py".
Еще один несложный пример класса: класс Zm, реализующий элементы кольца вычетов по модулю m, файл "Zm.py".
Список задач
-
Реализовать класс Polynomial, представляющий многочлен
произвольной степени с коэффициентами в поле рациональных
чисел. Должны быть реализованы операции сложения, умножения,
деления с остатком, вычисление наибольшего общего делителя
многочленов, производной многочлена, а также вычисление
многочлена с теми же корнями, свободного от кратных корней,
т.е. частного от
деления многочлена f на gcd(f, f').
Указание: в Python'е рациональные числа представлены классом Fraction в модуле fractions.
>>> from fractions import * >>> x = Fraction(3, 7) >>> y = Fraction(1, 5) >>> x + y Fraction(22, 35) - Та же задача, но для многочленов над полем Zp.
-
Реализовать класс "Элементы поля GFp2",
где p — простое число.
См. Конструкция конечного поля из p2 элементов. - Реализовать класс "Матрицы порядка m×n над полем рациональных чисел". Должны быть реализованы операции над матрицами, приведение матрицы к ступенчатому виду, вычисление ранга, а также для квадратной матрицы вычисление определителя и обратной матрицы и решение линейной системы с невырожденной матрицей.
- Та же задача, но для матриц над полем Zp.
Тема 2. SageMath — система компьютерной математики
2.1. Задачи по геометрии
Решения всех задач должны быть оформлены как функции на языке Sage (аналогичны функциям в языке Python). Например, в задаче "Нарисовать треугольник, вписанную окружность и точку Жергона" решение оформляется в виде функции, на вход которой подаются 3 точки и которая возвращает графический объект.
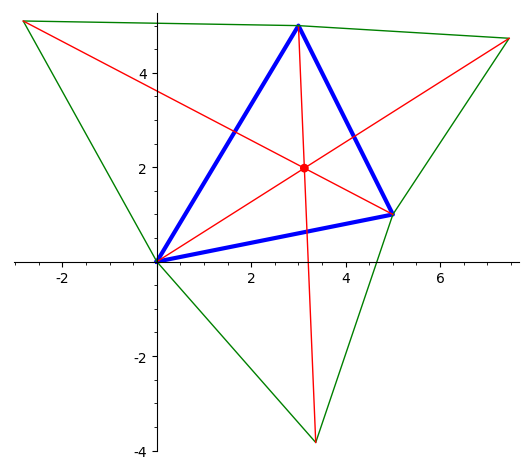
Пример решения задачи:
нарисовать треугольник, вписанную и описанную вокруг него окружности,
а также изобразить процесс их построения —
биссектрисы и серединные перпендикуляры.
Код sage-программы: "geometry.sage".
Пример использования функции:
sage: load("geometry.sage")
sage: a = vector([0, 0])
sage: b = vector([5, 1])
sage: c = vector([3, 5])
sage: drawTriangle(a, b, c)
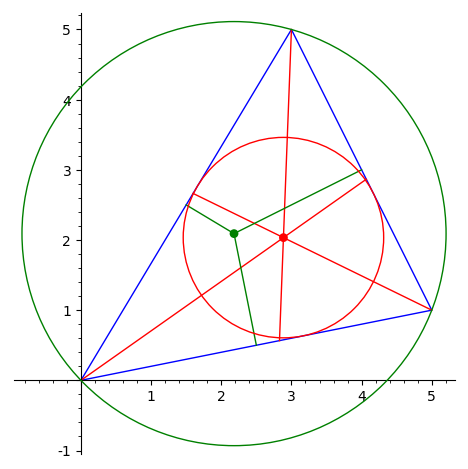
Список задач
-
Нарисовать треугольник, вписанную окружность и точку Жергона.
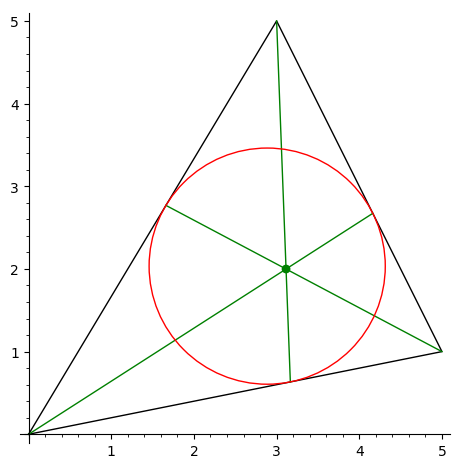
-
Нарисовать треугольник, три внешне вписанные окружности и точку Нагеля.
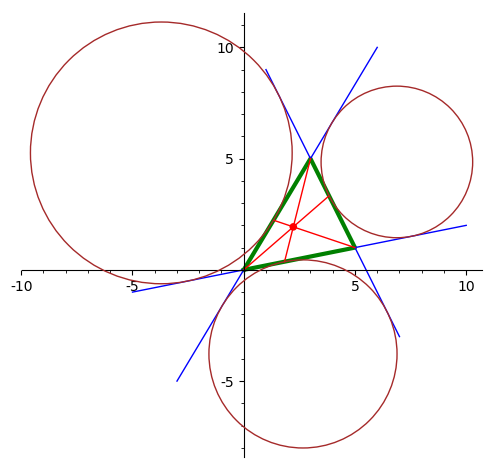
-
Нарисовать треугольник и точку Лемуана, которая построена как
точка, изогонально сопряженная к точке пересечения медиан.
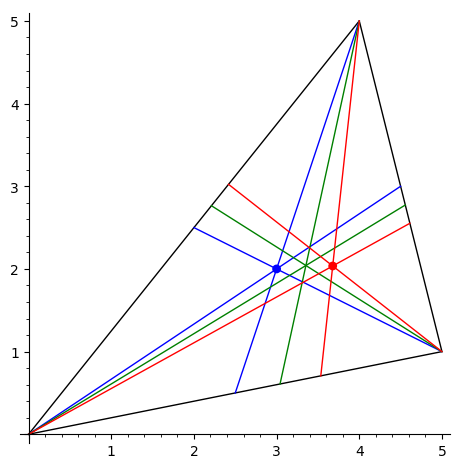
-
Нарисовать треугольник и точку Ферма-Торичелли (точка, минимизирующая
сумму расстояний до вершин треугольника), изобразив процесс ее
построения.
2.3. Кубическая интерполяция и построение кубических сплайнов
Рассматривается задача интерполяции, т.е. построения функции y = f(x) по заданным значениям в дискретном множестве узлов. Чаще всего такая функция строится как сплайн, состоящий из кубических многочленов, причем различаются C1-сплайны с непрерывной первой производной и C2-сплайны, у которых непрерывны первая и вторая производные.
Построение кубического C1-сплайна основано на следующем утверждении.
На следующем рисунке представлен график такого многочлена для значений
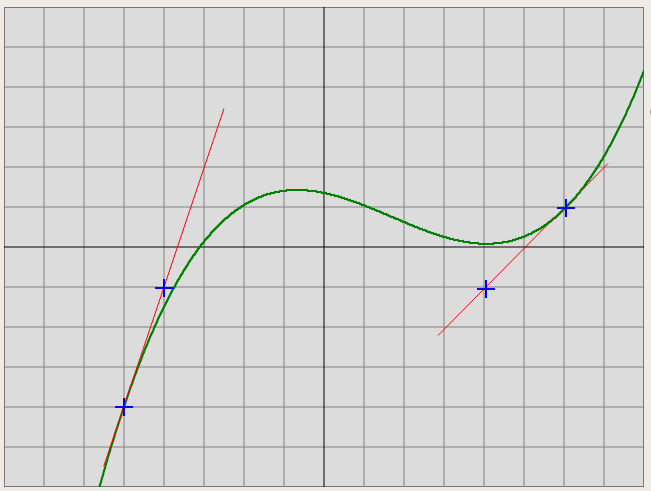
Можно самостоятельно вывести формулы для коэффициентов этого многочлена — например, выписав систему из 4-х уравнений и решив ее, либо каким-нибудь другим, более умным способом. Но в любом случае выражения получатся громоздкими, так что лучше предоставить эти вычисления SageMath. Сначала зададим переменные x0, x1, p0, p1, dp0, dp1, а также коэффициенты многочлена по возрастанию степеней a0, a1, a2, a3:
var("x0 x1 p0 p1 dp0 dp1")
var("a0 a1 a2 a3")
Зададим многочлен и его производную по x:
p(x) = a0 + a1*x + a2*x^2 + a3*x^3
dp(x) = derivative(p(x), x)
Выпишем 4 уравнения:
eq0 = (p(x = x0) == p0)
eq1 = (p(x = x1) == p1)
eq2 = (dp(x = x0) == dp0)
eq3 = (dp(x = x1) == dp1)
И теперь решим систему уравнений относительно неизвестных a0, a1, a2, a3, воспользовавшись функцией solve:
res = solve([eq0, eq1, eq2, eq3], [a0, a1, a2, a3])
Результатом является список решений, в данном случае состоящий из одного элемента (т.е. решение единственно). Решение — это список из 4-х уравнений, каждое из них имеет вид
sage: res[0][0]
a0 == -((dp1*x1 - p1)*x0^3 + p0*x1^3 + ((dp0 - dp1)*x1^2 + 3*p1*x1)*x0^2 -
(dp0*x1^3 + 3*p0*x1^2)*x0)/(x0^3 - 3*x0^2*x1 + 3*x0*x1^2 - x1^3)
Если нам нужно выражение для свободного члена, а не уравнение,
то можно воспользоваться методом rhs(), который возвращает
правую часть уравнения (от слов right hand side):
sage: res[0][0].rhs()
-((dp1*x1 - p1)*x0^3 + p0*x1^3 + ((dp0 - dp1)*x1^2 + 3*p1*x1)*x0^2 -
(dp0*x1^3 + 3*p0*x1^2)*x0)/(x0^3 - 3*x0^2*x1 + 3*x0*x1^2 - x1^3)
Получив выражения для коэффициентов многочлена интерполяции,
нетрудно нарисовать его график. Соответствующая программа
содержится в файле
"cubicPol.sage". Вот
пример ее выполнения:
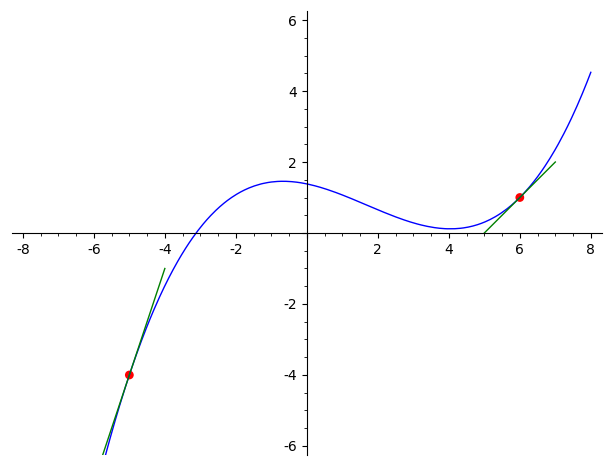
sage: load("cubicPol.sage")
sage: drawCubicInterpolation(xx0=-5, xx1=6, y0=-4, y1=1, dy0=3, dy1=1)
Задачи на построение кубического сплайна
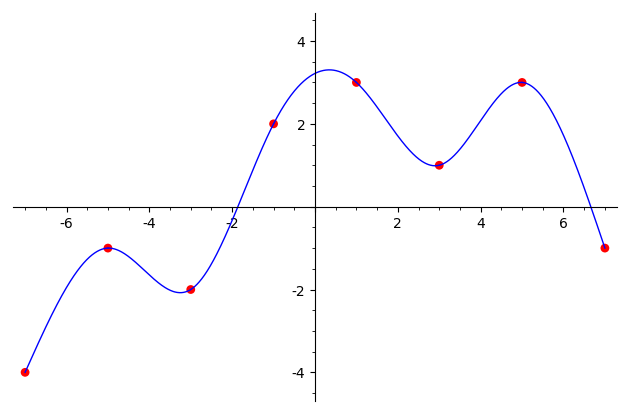
В задачах надо написать функцию (в смысле Python'а) с именем splineC1 или splineC2, на вход которой передается список пар. Каждая пара содержит координаты (xi, yi) i-го узла интерполяции, при этом координаты x идут в строго возрастающем порядке. Функция должна построить кубический C1 или С2-сплайн (с непрерывными только первыми производными или как первыми, так и вторыми производными). Пример использования функции:
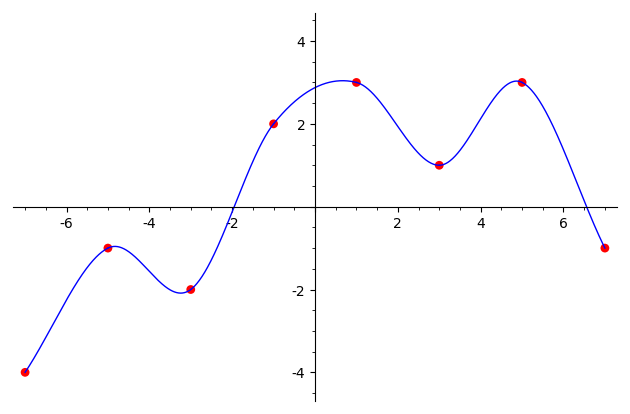
s = splineC1([(-7, -4), (-5, -1), (-3, -2), (-1, 2),
(1, 3), (3, 1), (5, 3), (7, -1)])
show(s, aspect_ratio=1)
(этот C1-сплайн показан на первой картинке ниже).
При построении C1-сплайна надо дополнительно задать производные в каждом узле, они определяются как полусумма значений тангенсов наклона звеньев ломаной слева и справа от узла. В начальном и конечном узлах производная задается как тангенс угла наклона звена ломаной, выходящего из этого узла.
При построении C2-сплайна решается система линейных уравнений, где неизвестными являются коэффициенты кубических многочленов, составляющих сегменты сплайна. Пусть дан n+1 узел:
2) правый сегмент сплайна принимает значение yi,
3) производные левого и правого сегментов сплайна равны между собой,
4) вторые производные левого и правого сегментов сплайна равны между собой.
2) значение второй производной начального сегмента сплайна в точке x0 равно нулю,
Студенты с нечетными номерами по журналу делают первую задачу, с четными — вторую.
Список задач
-
Построить C1-сплайн.
-
Построить C2-сплайн.
2.4. Коммутативная алгебра и базисы Гребнера
Рассматриваются кольца многочленов от нескольких переменных над полем комплексных чисел, конечные наборы многочленов в них, порождаемые ими идеалы и аффинные многообразия. Предполагаются известными теоремы Гильберта о конечности базисов и о нулях, а также теория базисов Гребнера.
Презентация к лекции по коммутативной алгебре: понятие фактор-кольца и фактор-алгебры, идеалы в кольцах и алгебрах, фактор-алгебры алгебр многочленов от нескольких переменных, теорема Гильберта о конечности базисов, теорема Гильберта о нулях, аффинные алгебраические многообразия, задаваемые идеалами, базис Гребнера идеала в алгебре многочленов, работа с многочленами и базисами Гребнера в SageMath.
Рекомендуется книга
а также пособие по математическому практикуму для группы алгебры
Список задач
Во всех задачах рассматривается алгебра многочленов от нескольких переменных над полем комплексных чисел.
- Даны два конечных набора многочленов. Определить, задают ли они одно и то же аффинное алгебраическое многообразие.
- Выяснить, имеет ли система алгебраических уравнений лишь конечное число решений (при этом хотя бы одно решение должно существовать).