Самостоятельная работа состоит в решении задач по темам, которые обсуждаются в лекциях. По каждой теме нужно решить одну задачу из предлагаемого списка. Номер задачи равен номеру студента в журнале по модулю n, где n — число задач по данной теме. Решения задач присылайте мне на электронную почту в виде одного или нескольких файлов, присоединенных к письму (если файлов много, то лучше присылать zip-архив с файлами в поддиректории). Адрес моей электронной почты:
vladibor266 (собака) gmail.com
Тема письма должна начинаться со слов "Душанбе 2025".

Журнал руппы ПМИиИ-4, весенний семестр 2025 г.

Тема 1. Классы для поддержки двумерной графики и геометрии

Мы используем классы R2Vector (вектор на плоскости) и R2Point (точка). Библиотека классов представленя двумя файлами:
R2Graph.h
R2Graph.cpp

Предполагается, что решение геометрических задач будет использовать только методы этих классов и не будет содержать никаких вычислений с координатами векторов и точек.

Пример программы, вычисляющей окружность, вписанную в треугольник:
"incircle.cpp"

Список задач на тему "Геометрия на плоскости"

1. Вычислить окружность, описанную вокруг треугольника.
   
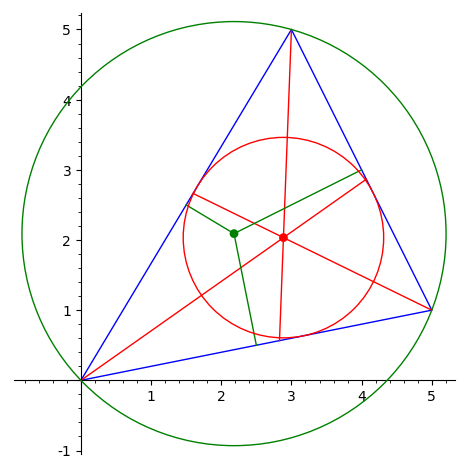
2. Вычислить точку Жергона треугольника.
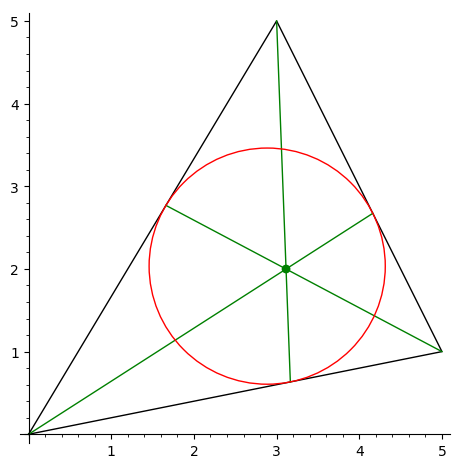
3. Вычислить точку Нагеля треугольника.
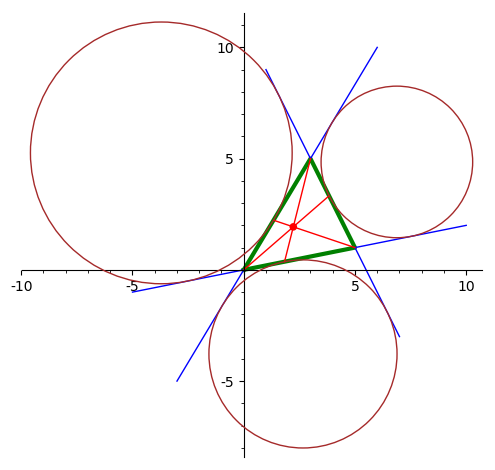
4. Вычислить точку Лемуана треугольника.

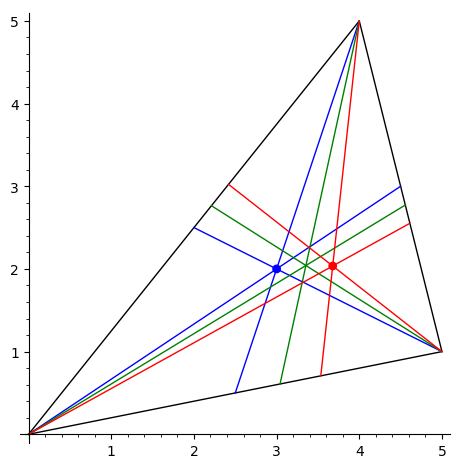
Тема 2. Классы в C++

Примеры классов

Рассмотренные ниже классы специально не реализованы до конца, чтобы можно было решать задачи.

1. Класс прямоугольных матриц: описание класса — файл "Matrix.h", реализация неинлайновых методов — файл "Matrix.cpp", тестовая программа — файл "matrixTest.cpp".
2. Библиотека классов для 2-мерной графики на плоскости: файлы "R2Graph.h", "R2Graph.cpp",
3. Класс "Многочлены на полем вещественых чисел": файлы "Polynomial.h", "Polynomial.cpp", тестовая программа — файл "PolynomialTest.cpp". Архив всех файлов: "Polynomial,zip".
4. Класс "Контур на плоскости". Контур представляет собой замкнутую ломаную без самопересечений, т.е. многоугольник на плоскости, не обязательно выпуклый. Направление обхода контура определяет его ориентацию: положительную, если обход против часовой стрелки (CCW — Counter Clockwise), отрицательную, если по часовой (CW). Вершины многоугольника хранятся как объекты типа R2Point в динамическом массиве типа std::vector<R2Point>.

   Помимо класса R2Contour, реализован также класс R2Polyline, представляющий незамкнутую ломаную на плоскости. Класс R2Contour наследуется из класса R2Polyline, а класс R2Polyline в свою очередь наследуется из класса std::vector<R2Point>.

   Файлы проекта: "R2Contour.h", "R2Contour.cpp", тестовая программа — файл "R2ContourTest.cpp", классы для поддержки 2-мерной геометрии — "R2Graph.h", "R2Graph.cpp", Архив всех файлов: "R2Contour,zip".

Список задач на тему "Классы в C++"

Студент должен решить ту задачу, номер которой совпадает по модулю 4 с его номером в журнале.

1. Реализовать до конца класс Матрицы. Должны быть реализованы операции над матрицами (сложение, вычитание, умножение), вычисление ранга и определителя матрицы, вычисление обратной матрицы. Для квадратной невырожденной матрицы A и вектора B должно быть реализовано решение линейной системы уравнений A·X = B.
2. Реализовать до конца класс многочленов над полем вещественных чисел. Должны быть реализованы операции над многочленами, включая сложение, вычитание и умножение двух многочленов, умножение многочлена на число, деление с остатком двух многочленов, а также вычисление производной многочлена, значения многочлена в заданной точке и наибольшего общего делителя двух многочленов.
3. Реализовать до конца класс "Контур на плоскости". Вершины ломаной, определяющей контур, надо хранить как объекты типа R2Point. Должно быть реализовано определение ориентации контура, ориентирование контура (при необходимости изменение направления его обхода), вычисление площади и площади со знаком контура, его периметра, центра тяжести вершин и центра тяжести как плоской фигуры, определение, лежит ли заданная точка внутри контура, вычисление угла, под которым контур виден из заданной точки, и другие естественные для этого класса методы.
4. Реализовать класс "Треугольник на плоскости". Вершины треугольника надо хранить как объекты типа R2Point. Должно быть реализовано определение ориентации треугольника, ориентирование треугольника (при необходимости изменение направления его обхода), вычисление площади и площади со знаком треугольника, его периметра, центра тяжести, а также вычисление описанной и вписанной окружностей. Для произвольной точки нужно уметь определять, лежит ли точка внутри или вне треугольника. Также нужно уметь вычислять пересечение треугольника и прямой, а также угол, под которым треугольник виден из заданной точки.

Для реализованного класса надо написать тестовую консольную программу, которая вводит объект или несколько объектов класса с клавиатуры, вызывает тестируемые методы и печатает результаты.

Сортировка

Лекция Алгоритмы сортировки (презентация)

Генерация случайных чисел

Скорость работы алгоритмов сортировки интересно оценивать на больших массивах, содержащих миллионы элементов. Для заполнения таких массивов мы используем генераторы случайных чисел. Древняя функция rand() из ANSI-библиотеки языка C недостаточно хороша (например, при генерации случайных точек в многомерном пространстве большая часть из них содержится в некоторой гиперплоскости). Для того, чтобы программа не работала детерминированно при разных запусках, раньше использовалась функция srand для установки начального элемента псевдослучайной последовательности, в качестве случайного значения функции srand обычно передавалось время в секундах с начала эпохи 1 января 1970 г., что также недостаточно для современных программ. В современной стандартной библиотеке языка C++ содержатся намного более качественные функции для генерации случайных чисел. Типичная схема генерации случайных целых и вещественных чисел в заданных диапазонах иллюстрируется следующей программой "randDevice.cpp":

#include <iostream>
#include <random>

int main() {
    std::random_device seed;
    std::mt19937 gen(seed());
    std::uniform_int_distribution<int> intRange(1, 100);
    std::uniform_real_distribution<double> realRange(-10., 10.);

    std::cout << "Random integer numbers:" << std::endl;
    for (int i = 0; i < 20; ++i) {
        int randNumber = intRange(gen);
        if (i > 0) {
            // Delimiter
            if (i%5 == 0)       // 5 numbers in a line
                std::cout << std::endl;
            else
                std::cout << ' ';
        }
        std::cout << randNumber;
    }
    std::cout << std::endl;

    std::cout << "Random real numbers:" << std::endl;
    for (int i = 0; i < 20; ++i) {
        double randNumber = realRange(gen);
        if (i > 0) {
            // Delimiter
            if (i%5 == 0)       // 5 numbers in a line
                std::cout << std::endl;
            else
                std::cout << ' ';
        }
        std::cout << randNumber;
    }
    std::cout << std::endl;

    return 0;
}

Описания функций для генерации случайных чисел содержатся в заголовочном файле random:

    #include <random>

    std::random_device seed;

    std::mt19937 gen(seed());

Однако обычно нам нужны числа в заданном диапазоне. Для этого можно применять объекты типа std::uniform_int_distribution<int> для генерации целых чисел или std::uniform_real_distribution<int> для генерации вещественных чисел:

    std::uniform_int_distribution<int> intRange(1, 100);
    std::uniform_real_distribution<double> realRange(-10., 10.);

        int randNumber = intRange(gen);

        double randNumber = realRange(gen);

Вот результат работы приведенной выше программы "randDevice.cpp":

    >g++ -o randDevice randDevice.cpp
    >./randDevice
    Random integer numbers:
    100 39 73 89 81
    78 58 91 10 61
    84 16 44 55 48
    93 15 67 54 30
    Random real numbers:
    -5.75583 -6.79703 9.89776 0.351352 -5.17714
    -3.1965 -5.16208 6.71477 2.46811 7.78662
    4.96462 8.28746 -1.036 -0.750713 5.14964
    -2.7142 8.38426 4.50047 3.19789 -6.55677

Задачи по теме "Сортировка"

Нужно решить одну задачу, номер которой совпадает по модулю 3 с номером студента в журнале. В качестве заготовки следует использовать файл "tstSort.cpp", содержащий функции генерации случайных массивов и их печати, а также прототипы функций сортировки разными методами. Реализация дана только для функции сортировки insertionSort и нескольких вспомогательных функций, таких как bubbleDown и merge, реализации остальных алгоритмов сортировки оставлена в качестве задач.

1. Написать функцию сортировки массива методом пирамиды HeapSort. Прототип функции:

   void heapSort(
       std::vector::iterator i0,
       std::vector::iterator i1
   );
   

2. Написать функцию сортировки массива методом слияния MergeSort, используя нисходящую (рекурсивную) схему реализации. Прототип функции:

   void mergeSortTopBottom(
       std::vector::iterator i0,
       std::vector::iterator i1,
       std::vector::iterator* tmpMemory = nullptr
   );
   

3. Написать функцию сортировки массива методом слияния MergeSort, используя восходящую (итеративную) схему реализации. Прототип функции:

   void mergeSortBottomTop(
       std::vector::iterator i0,
       std::vector::iterator i1,
       std::vector::iterator* tmpMemory = nullptr
   );
   

Деревья поиска, почти сбалансированные деревья.
Красно-черные деревья и реализация множества на их основе

Содержание лекции

Пусть нам надо реализовать множество (или нагруженное множество), на элементах которого определен линейный порядок. Тогда элементы множества (или пары (ключ, значение) в случае нагруженного множества) можно расположить в вершинах бинарного дерева. При этом значения в вершинах должны быть упорядочены следующим образом:

• для любой нетерминальной вершины V значения во всех вершинах левого поддерева с корнем V должны быть меньше, чем значение в вершине V;
• значения во всех вершинах правого поддерева с корнем V должны быть больше, чем значение в вершине V.

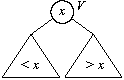
Для такого дерева можно применять алгоритм бинарного поиска, аналогичный поиску в упорядоченном массиве. Поэтому подобные деревья называют деревьями поиска. Пример дерева поиска приведен на рисунке; его вершины содержат целые значения.

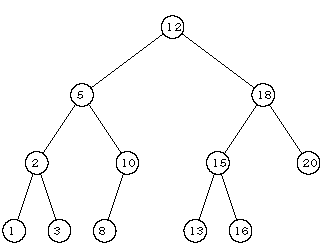
Опишем более подробно устройство дерева поиска. Каждая вершина дерева представляет собой следующую структуру:

    template 
    class TreeNode {
    public:
        TreeNode* left;   // Указатель на левого сына
        TreeNode* right;  // Указатель на правого сына
        TreeNode* parent; // Указатель на отца
        TreeValue value;  // Значение в узле
                          // или пара (ключ, значение ключа)
    };

В большинстве алгоритмов удобно считать, что у любой вершины v дерева, в том числе корневой, есть родительская вершина. В противном случае пришлось бы многократно рассматривать отдельно случаи, когда указатель v->parent равен нулю. Используется следующий прием: вводится специальная "заголовочная" вершина header, которая присутствует даже у пустого дерева. Корень непустого дерева является левым сыном вершины header. Поле header->right всегда содержит нулевое значение. Всюду ниже мы будем считать, что используется заголовочная вершина header, левым сыном которой является корень дерева.

Алгоритм поиска

Запишем на псевдокоде алгоритм поиска в дереве. Мы ищем элемент x в поддереве с корнем root. Результатом поиска является вершина *node, определяемая следующим образом:

• если элемент x содержится в множестве, то *node — указатель на вершину, содержащую x;
• если элемент x не содержится в множестве, то *node — указатель на вершину, которая при добавлении x к множеству должна стать родительской для новой вершины V, содержащей x. Новая вершина V добавляется как терминальная, а у найденной вершины *node отсутствует левый сын, если x меньше значения в вершине *node, или правый сын, если больше.

int find(
    Вход:  E x,             // искомый элемент,
           TreeNode* root,  // указатель на вершину поддерева
    Выход: TreeNode** node  // найденная вершина
)
начало алгоритма
    TreeNode* v, vp;
    E y;
    int res = -1;
    v = root;
    vp = root;
    цикл пока v != 0
        y = v->value;       // y = значение в вершине v
        если x == y         // x равно значению в вершине =>
            *node = v;      //   запомним указатель на вершину
            return 0;       //   успешное завершение
        иначе если x < y    // x меньше значения в вершине =>
            vp = v;         //   запомним указатель на отца
            res = -1;       //   запомним результат сравнения
            v = v->left;    //   переходим к левому сыну
        иначе               // иначе     // x > y
            vp = v;         //   запомним указатель на отца
            res = 1;        //   запомним результат сравнения
            v = v->right;   //   переходим к правому сыну
        конец если
    конец цикла
                            // x не содержится в дереве
    *node = vp;             // *node = указатель на отца
    return res;
конец алгоритма

Число сравнений в данном алгоритме не превышает высоты дерева h. Таким образом, время работы алгоритма равно O(h).

Алгоритм добавления элемента

Добавление элемента к упорядоченному дереву легко реализуется с помощью алгоритма поиска. Сначала применяется описанный выше алгоритм find. Если вершина найдена, то в случае обычного множества ничего делать не надо; в случае нагруженного множества надо лишь изменить нагрузку элемента. Для простоты мы ограничимся в дальнейшем случаем обычного множества.

Если элемент не содержится в дереве, то алгоритм find находит вершину, которая должна стать родительской для новой вершины. Новая вершина, содержащая добавляемый элемент множества, становится левым или правым сыном найденной вершины в зависимости от величины добавляемого элемента в сравнении с элементом в родительской вершине. Для определения того, каким сыном должен стать новый узел, используется значение последнего сравнения, которое возвращается алгоритмом find. Запишем на псевдокоде алгоритм insert добавления вершины после выполнения поиска.

алгоритм insert(
    Вход:  TreeNode* parentNode, // родительская вершина,
                                 // найденная при поиске
           E x,          // добавляемый элемент
           int compare   // результат сравнения x со
)                        //     значением в вершине parentNode
начало алгоритма
    TreeNode* n = new TreeNode; // создать новую вершину дерева
    n->left = 0; n->right = 0;  // новая вершина терминальная
    n->parent = parentNode;     // она будет ребенком найденной вершины
    n->value = x;
    если compare < 0            // если x меньше, чем значение в вершине
        parentNode->left = n;   //     добавляем n как левого сына
    иначе                       // иначе
        parentNode->right = n;  //     добавляем n как правого сына
    конец если
конец алгоритма

Поиск минимального и максимального элементов поддерева

Алгоритмы поиска минимального и максимального элементов используются в алгоритме обхода вершин дерева в соответствии с их упорядоченностью. Для поиска минимальной вершины начинаем с корня поддерева и спускаемся от текущей вершины к ее левому сыну, пока таковой имеется. Алгоритм заканчивается, когда у текущей вершины левого сына нет. Отметим, что минимальная вершина дерева не обязательно должна быть терминальной, у нее может быть правый сын. Выпишем на псевдокоде алгоритм поиска минимальной вершины.

TreeNode* minimalNode(
    Вход: TreeNode* subTreeRoot // указатель на вершину поддерева
)
начало алгоритма
    RBTreeNode* x = subTreeRoot;
    цикл пока (x != 0 && x->left != 0)
        x = x->left;
    конец цикла
    return x;
конец алгоритма

Алгоритм обхода вершин дерева поиска

Для упорядоченного дерева очень важен алгоритм обхода вершин в соответствии с их порядком. Обход начинается с вершины, содержащей минимальное значение. Затем находим вершину, содержащую следующее значение, и так далее. Алгоритм заканчивается, когда очередной вершиной является "заголовочная" вершина header (родитель для корня дерева).

Для обхода используется алгоритм nextNode, который по данному указателю на вершину node находит указатель на вершину, содержащую следующее значение. Отметим, что для максимальной вершины дерева следующей является "заголовочная" вершина header.

Алгоритм реализуется очень просто: если у вершины node есть правый сын, то возвращается минимальная вершина правого поддерева; иначе, если node является левым сыном своего отца, то возвращаем указатель на отца. Наконец, если оба эти условия не выполняются, т.е. node есть правый сын своего отца и у него нет правого сына, то в цикле идем вверх по дереву, пока текущий узел является правым сыном своего отца. После цикла текущий узел является левым сыном своего отца. Возвращаем ссылку на отца.

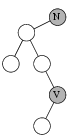
Приведенные ниже рисунки иллюстрируют три эти случая. Буквой V обозначена текущая вершина, буквой N — вершина, которая содержит следующее значение. Отметим, что алгоритм нигде не использует сравнения значений, содержащихся в вершинах дерева.

Случай 1: у вершины V есть правый сын.

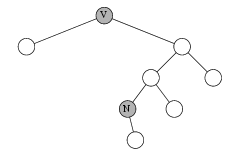
Случай 2: у вершины V нет правого сына, и она является левым сыном своего отца.

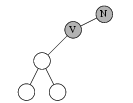
Случай 3: у вершины V нет правого сына, и она является правым сыном своего отца.

TreeNode* nextNode(
    Вход: TreeNode* node
)
начало алгоритма
    если (node->right != 0)                 // у node есть правый сын
        return minimalNode(node->right)
    иначе если (node == node->parent->left) // node -- левый сын
        return node->parent;
    иначе
        RBTreeNode* x = node->parent;
        цикл пока (x == x->parent->right)   // пока x -- правый сын
            x = x->parent;                  //     идем вверх по дереву
        конец цикла
        утв: x -- левый сын своего отца
        return x->parent;
    конец если
конец алгоритма

Алгоритм previousNode, который по указателю на вершину дерева находит указатель на предыдущую вершину, реализуется аналогично.

Сбалансированные деревья

Рассмотрим произвольное дерево поиска. В худшем случае время работы алгоритма поиска равняется длине максимального пути от корня дерева к терминальной вершине, т.е. высоте дерева. Для того, чтобы поиск выполнялся по возможности быстрее, дерево должно иметь минимальную высоту при заданном числе вершин. Для этого нужно, чтобы все возможные пути к терминальным вершинам имели бы примерно одинаковую длину (более точно, для любой вершины дерева число вершин в ее левом и правом поддеревьях почти совпадали).

Перейдем к строгим определениям. Удобно считать, что у каждой вершины дерева есть ровно два сына. Для этого добавим к дереву внешние, или нулевые вершины. Если у какой-либо вершины дерева отсутствует левый или правый сын, то добавляем внешнюю вершину и считаем ее левым или правым сыном соответственно. Для терминальных вершин добавляются два внешних сына. Внешние вершины будем также называть листьями. Обычные вершины дерева будем называть собственными вершинами, причем слово "собственные" иногда будем опускать.

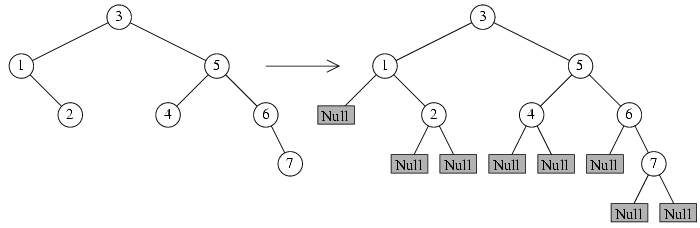
При программировании на Си внешние дети вершины t соответствуют нулевым значениям указателей t->left и t->right. Добавление внешних вершин к дереву показано на рисунке. Внешние вершины (нулевые вершины, листья) изображены прямоугольниками серого цвета, внутри которых написано слово Null, символизирующее нулевой указатель.

Длиной пути от корня дерева к внешней вершине будем называть число собственных вершин этого пути (т.е. последняя внешняя вершина не считается).

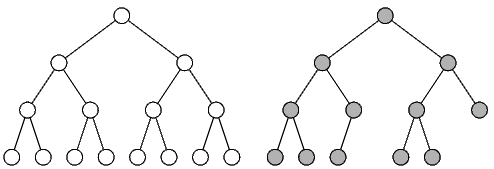
Определение. Дерево называется сбалансированным, или полным, если длины всех путей от корня к внешним вершинам равны между собой. Дерево называется почти сбалансированным, если длины всевозможных путей от корня к внешним вершинам отличаются не более, чем на единицу.

На рисунке приведены примеры сбалансированного и почти сбалансированного деревьев.

Справедливы следующие утверждения (их доказательства опущены ввиду тривиальности).

Предложение 1. Число собственных вершин в сбалансированном дереве высоты h равно 2^h-1.

Следствие 2. Высота сбалансированного дерева, содержащего n собственных вершин, равна log₂(n+1).

Предложение 3. Число вершин произвольного дерева не превосходит числа вершин сбалансированного дерева той же высоты.

Следствие 4. Для высоты h произвольного дерева, содержащего n вершин, справедливо неравенство: h ≥ log₂(n+1).

Эффективность реализации множества с помощью дерева поиска зависит от текущей высоты дерева, т.к. при выполнении большинства операций сначала происходит поиск элемента, а время работы алгоритма поиска пропорционально высоте. При заданном числе вершин n наименьшую высоту имеет сбалансированное или почти сбалансированное дерево (последнее в случае, когда n не равно 2^h-1). Если дерево почти сбалансировано, то время поиска не превосходит log₂(n) + 1. Однако в случае произвольного дерева время поиска может в худшем случае линейно равняться n (если дерево вытянуто в прямую линию). Поэтому при добавлении элементов к множеству желательно перестраивать дерево так, чтобы сохранялось то или иное свойство, близкое к сбалансированности. Это гарантирует быстрое выполнение поиска.

Предложение 5. Пусть существует константа C ≥ 1 такая, что длины всех путей от корня к внешним вершинам (листьям) дерева отличаются не более чем в C раз. Более точно, пусть m₀ — длина минимального пути, m₁ — максимального, и выполняется неравенство m₁ ≤ C·m₀. Тогда высота дерева не превосходит C log₂(n+1), где n — число собственных вершин дерева.

Доказательство.  Пусть h — высота дерева. Из условия предложения вытекает, что длины всех путей от корня к листьям дерева не меньше чем h/C. Следовательно, дерево содержит сбалансированное поддерево высоты l ≥ h/C. Поэтому число n всех вершин дерева не меньше, чем число вершин сбалансированного поддерева. По предложению 1, число вершин сбалансированного поддерева высоты l равно 2^l-1. Следовательно,

  n ≥ 2^l-1 ≥ 2^h/C-1,
  log₂(n+1) ≥ h/C,
  h ≤ C log₂(n+1).

Предложение доказано.

Будем называть дерево, удовлетворяющее условию предложения 5, почти сбалансированным с баланс-фактором C, где C ≥ 1. Для таких деревьев время поиска логарифмически зависит от числа вершин:

  t = O(log₂n),

где константа в представлении O-большого равна C. В практическом программировании константы в оценке времени работы алгоритма не очень важны — существенна лишь зависимость времени работы от n. Логарифмическая зависимость — наилучшая из всех возможных, поэтому в классе почти сбалансированных деревьев с баланс-фактором C поиск выполняется за оптимальное время.

Можно показать, что при добавлении случайных элементов к дереву поиска с помощью рассмотренного выше алгоритма, в котором новая вершина добавляется как терминальная после выполнения поиска родительской вершины, сбалансированность "в среднем" сохраняется, т.е. с большой вероятностью баланс-фактор не будет превышать, скажем, двух. Тем не менее существует несколько схем модификации деревьев после добавления и удаления вершин, при которых баланс-фактор всегда будет ограничен при любом сценарии добавления. Наиболее популярны два класса сбалансированных деревьев: AVL-деревья и красно-черные деревья.

AVL-деревья названы так в честь двух авторов, впервые предложивших их: Адельсона--Вельского и Ландиса. Каждая вершина AVL-дерева хранит дополнительно разность высот ее левого и правого поддеревьев, причем эта разность в AVL-дереве может принимать лишь три значения: -1, 0, 1. Можно показать, что для AVL дерева с достаточно большим числом вершин длина максимального пути корня к внешнему листу не превышает константы 1.5, умноженной на длину минимального пути, т.е. баланс-фактор в смысле использованного выше определения равен 1.5. Следовательсно, поиск в AVL-деревьях осуществляется за логарифмическое время.

Красно-черные деревья

В красно-черных деревьях для балансировки используются цвета вершин. Каждая вершина красно-черного дерева окрашена либо в черный, либо в красный цвет, причем выполняются следующие условия:

• корень дерева окрашен в черный цвет;
• у красной вершины дети черные (если они есть);
• всякий путь от корня дерева к внешней вершине (листу) содержит одно и то же число черных вершин.

Последнее свойство означает сбалансированность красно-черного дерева по черным вершинам. Количество черных вершин на пути от корня дерева к внешней вершине иногда называют черной высотой красно-черного дерева, последнее свойство означает, что определенная таким образом черная высота не зависит от конкрентого пути.

Для удобства описания алгоритмов мы будем считать также, что все внешние вершины окрашены в черный цвет, а заголовочная вершина дерева (та, которая является родительской для корня дерева) — в красный.

Пример красно-черного дерева приведен на рисунке. Черные вершины изображаются кружками серого цвета, красные вершины — белого.

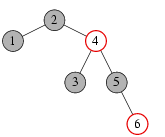
Пусть h_b — черная высота красно-черного дерева, т.е. количество черных вершин в произвольном пути от корня дерева к внешней вершине (не включая саму внешнюю вершину). По определению красно-черного дерева, эта величина определена корректно (не зависит от пути). Для дерева, изображенного на рисунке, h_b=2. Поскольку любой путь от корня к внешней вершине начинается с черной вершины (в красно-черном дереве корень всегда черный) и не может содержать двух красных вершин подряд (у красной вершины дети обязательно черные), то длина любого пути не превосходит 2h_b. С другой стороны, длина минимального пути к внешней вершине не меньше чем h_b. Таким образом, в случае красно-черного дерева для длин m₀ и m₁ минимального и максимального путей к внешним вершинам выполняются неравенства

  m₁ ≤ 2 h_b,

  m₀ ≥ h_b,

  m₁ ≤ 2 m₀.

Таким образом, красно-черное дерево является почти сбалансированным с баланс-фактором 2. Из предложения 5 вытекает логарифмическая оценка на высоту h красно-черного дерева, содержащего n вершин:

  h   ≤ 2 log₂(n+1).

Поиск элемента в красно-черном дереве осуществляется за логарифмическое время:

  t = O(log₂n),

где константа в представлении O-большого равна двум.

Добавление элементов в красно-черное дерево

При добавлении нового элемента к красно-черному дереву мы сначала применяем обычный алгоритм добавления вершины к дереву поиска, который был рассмотрен выше (алгоритм insert). Новая вершина (она в рассмотренном алгоритме всегда является терминальной) окрашивается в красный цвет. Если родительская вершина для добавленной имеет черный цвет, то все свойства красно-черного дерева при этом сохраняются, и никаких дополнительных действий не требуется. Однако, если родительская вершина красная, то нарушается требование того, что дети красной вершины должны быть черными, и нужно выполнить процедуру восстановления структуры красно-черного дерева. Обычно эта процедура называется восстановлением баланса или ребалансировкой. В алгоритме ребалансировки с деревом совершаются локальные действия, не меняющие упорядоченности его вершин. Действия бывают двух типов:

• перекрашивание вершин дерева,
• вращение вершины дерева влево или вправо.

Операция вращения вершины дерева

Определим преобразования вращения. Левое вращение вершины x :

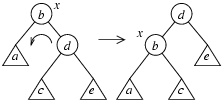
Правое вращение вершины x :

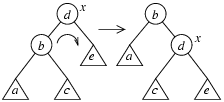
По рисункам видно, что оба преобразования не меняют упорядоченности вершин дерева. Преобразования носят локальный характер, при их выполнении меняется лишь фиксированное число ссылок в вешинах дерева вблизи вершины, которая "вращается" влево или вправо. Запишем на псевдокоде процедуру вращения вершины x влево.

void rotateLeft(
    Вход: TreeNode* x
)
начало алгоритма
    TreeNode* y = x->right; // y -- правый сын x
    утв: y != 0

    // Узлы x и y меняются местами (подчиненный "y" бывшего
    // начальника "x" становится новым начальником)
    // Делаем y корнем модифицированного поддерева
    TreeNode* p = x->parent;
    y->parent = p;
    если (x == p->left) // x -- левый сын своего отца
        p->left = y;
    иначе               // x -- правый сын своего отца
        p->right = y;
    конец если

    // Бывший левый сын узла "y" становится правым сыном узла "x"
    x->right = y->left;
    если (y->left != 0)
        y->left->parent = x;
    конец если

    // Бывший начальник "x" становится подчиненным нового начальника "y"
    y->left = x;
    x->parent = y;
конец алгоритма

Правое вращение вершины x реализуется аналогично.

Операция левого или правого вращения вершины во многих случаях позволяет "исправить" балансировку дерева, как показывает следующий пример. В нем мы применяем вращение вершины x влево.

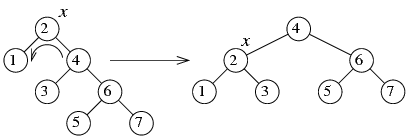
Восстановление структуры красно-черного дерева после добавления вершины (ребалансировка)

В процедуре ребалансировки рассматриваются 6 различных случаев. В случаях 1-3 отец узла x является левым сыном своего отца, т.е. деда x.

1. У узла x есть красный "дядя" (брат отца x). При этом x может быть левым или правым сыном своего отца — случаи эти рассматриваются аналогично.
   
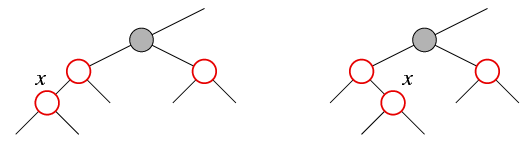
2. У узла x "дядя" (брат отца) либо черный, либо его вообще нет (т.е. сыном является лист или внешний узел, который мы также считаем черным), и узел x является правым сыном своего отца.
   
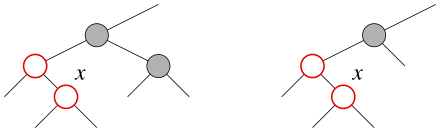
3. У узла x "дядя" (брат отца) либо черный, либо его вообще нет, и узел x является левым сыном своего отца.
   

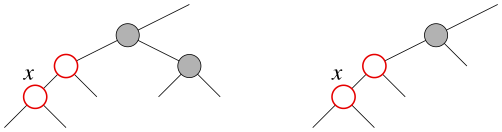
Случаи 4-6 зеркально симметричны случаям 1-3, в них отец узла x является правым сыном своего отца, т.е. деда x. Рассматриваются они аналогично случаям 1-3 заменой слова "левый" на "правый" и обратно, так что мы их описывать не будем.

Укажем, какие действия выполняются в каждом из случаев 1-3 для восстановления балансировки дерева.

Случай 1 (красный дядя)

Этот случай наиболее прост:

• перекрашиваем отца и дядю узла x в черный цвет;
• перекрашиваем деда узла x в красный цвет;
• перемещаем метку x вверх по дереву на деда узла x: и переходим в цикле к восстановлению нового узла x (деда предыдущего x)
       x = x->parent->parent
  

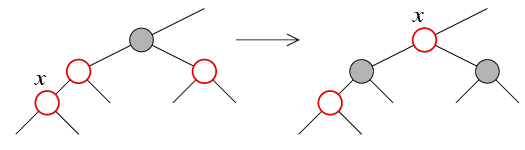
Цикл завершается, либо когда мы достигли корня дерева (если корень был перекрашен в красный цвет, то надо перекрасить его обратно в черный), либо когда отец узла x черный.

Случай 2 (дядя черный или его вообще нет, узел x является правым сыном своего отца)

Этот случай сводится к случаю 3 путем следующих преобразований:

• перемещаем метку x вверх по дереву: x = x->parent;
• левое вращение x.

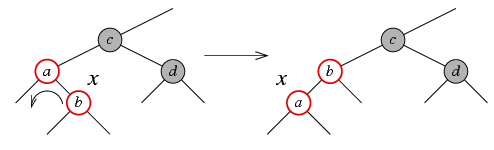
Случай 3 (дядя черный или его вообще нет, узел x является левым сыном своего отца)

В этом случае выполняются следующие действия:

• перекрашиваем отца узла x в черный цвет;
• перекрашиваем деда (т.е. отца отца) x в красный;
• выполняем правое вращение деда x.

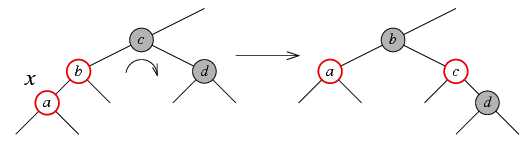
Отметим, что всего в процедуре восстановления структуры красно-черного дерева (ребалансировки) может выполняться не более O(h) операций; поскольку для красно-черного дерева h  ≤  2 log₂(n+1), получаем, что время выполнения ребалансировки равно O(log₂ n). В этой процедуре выполняются перекрашивание узлов дерева и операции вращения, причем общее число вращений — не больше двух (одно вращение в случае 3 и два в случае 2).

Проект "RBTree": файл RBTree.zip