Нахождение локального минимума функции от нескольких переменных:
метод градиентного спуска и его модификации

Постановка задачи

Дана непрерывно дифференцируемая функция от нескольких переменных: $$ f: \Bbb{R}^n \to \Bbb{R} $$ Нужно найти минимум этой функции — точнее, точку $x$, в которой функция принимает минимальное значение. Мы будем искать точку локального минимума $x_*$, в которой градиент функции равен нулевому вектору или очень мал: $$ ||\nabla f(x_*)|| < \varepsilon. $$

Метод градиентного спуска

В методе градиентного спуска нам дается начальное приближение $x_0$. Предполагается, что в некоторой окрестности минимума функция выпукла вниз и точка $x_0$ принадлежит этой окрестности. Метод градиентного спуска носит итерационный характер: мы вычисляем последовательность приближений $x_0, x_1, x_2, x_3, \dots$, в которой текущая точка движется к точке минимума. Количество итераций заранее неизвестно, и даже сходимость метода гарантирована далеко не всегда. Хотя теоретически можно указать достаточные условия сходимости, а также оценить ее скорость.

Параметром в методе градиентного спуска является размер шага $\alpha$, в методах машинного обучения его называют также скоростью обучения — learning rate. Пусть $x_k$ — очередное приближение, тогда следующее приближение вычисляется по формуле $$ x_{k+1} = x_k - \alpha \cdot \nabla f(x_k) $$ Здесь $\nabla f(x_k)$ — вектор градиента функции $f$ в точке $x_k$, указывающий направление роста функции. Вектор противоположного направления $-\nabla f(x_k)$ иногда называют антиградиентом. Мы смещаемся в направлении убывания функции на величину $\alpha \cdot \nabla f(x_k)$, пропорциональную длине вектора градиента, здесь $\alpha$ — коэффициент пропорциональности. Чем больше $\alpha$, тем быстрее процесс сходится, однако слишком большое значение $\alpha$ может привести к осцилляции либо вообще к уходу от точки минимума. Примитивное объяснение состоит в том, что при большой величине шага текущая точка проскакивает область убывания функции вблизи очередной точки итерации и входит в зону возрастания, затем возвращается назад, опять проскакивая область убывания и т.д., причем процесс может даже не сходиться. 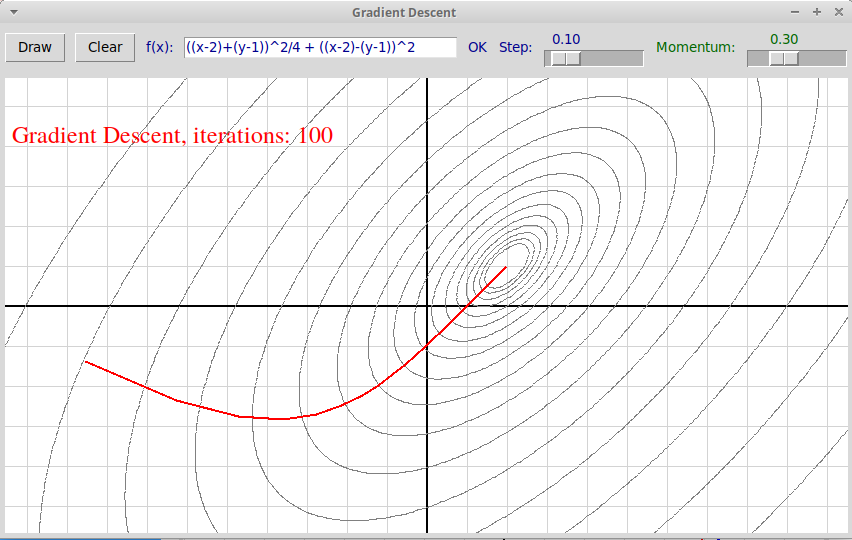Такая осцилляция видна на следующих скриншотах программы нахождения минимума: в первом случае коэффициент $\alpha = 0.1$ невелик и программа находит хорошее приближение для точки минимума, а траектория точки получается достаточно гладкой (число итераций не более 100, $\varepsilon = 10^{-5}$):

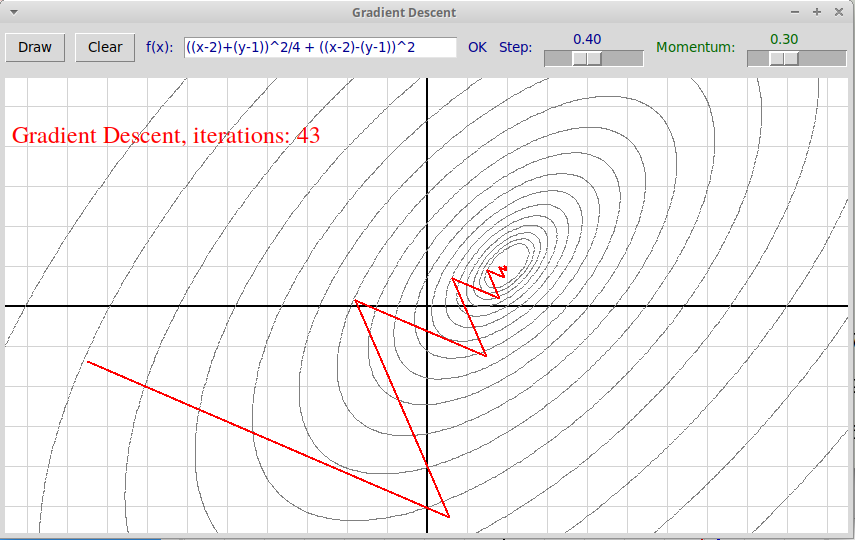
Однако при большей величине шага $\alpha = 0.4$ начинается осцилляция:

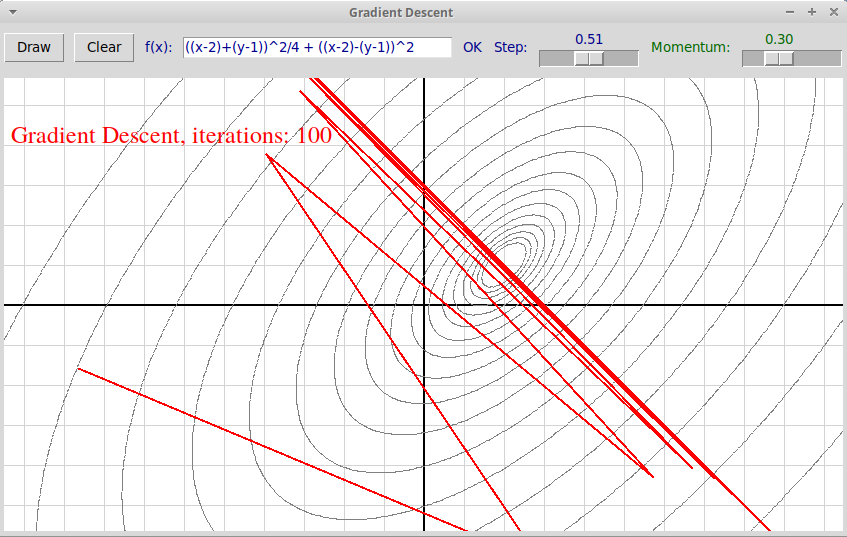
В данном случае процесс все еще сходится, но уже при $\alpha = 0.5$ траектория не попадает в точку минимума, а амплитуда осцилляций стремится к бесконечности:

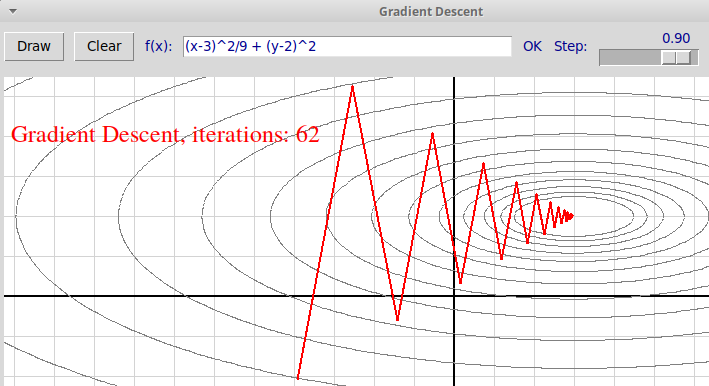
Отметим, что осцилляция чаще всего возникает, когда линии уровня функции $f(x)$ в окрестности точки минимума предсталяют собой сильно вытянутые эллипсы (в $n$-мерном случае эллипсоиды с сильно отличающимися длинами полуосей). Это происходит в том случае, когда мера обусловленности матрицы вторых произодных функции (Гессиана) велика, т.е. велико отношение ее максимального собственного значения к минимальному. В двумерном случае поверхность уровня функции представляет собой сильно вытянутую яму, больше напоминающую овраг, и текущая точка перескакивает с одного берега оврага на другой и обратно:

Достаточные условия сходимости метода градиентного спуска и оценка скорости сходимости

Пусть известно, что в некоторой окрестности точки минимума функция $f(x)$ выпукла вниз и начальное приближение $x_0$ принадлежит этой окрестности. Пусть также функция удовлетворяет условию Липшица на ее градиент с константой $L$: $$ ||\nabla f(x_1) - \nabla f(x_2)|| \le L ||x_1 - x_2|| $$ При размере шага $\alpha < 2/L$ метод градиентного спуска сходится к точке минимума $x_*$, причем справедлива следующая оценка сверху для числа итераций $N$: $$ N = O(LR^2/\varepsilon), $$ где $R = ||x_0 - x_*||$ — расстояние от точки начального приближения до точки минимума.

На практике параметр "размер шага" (или learning rate) полагается равным $1/L$, если, конечно, есть возможность оценить $L$.

Однако построены несложные модификации метода градиентного спуска, работающие значительно быстрее, причем вероятность осцилляций в них гораздо ниже. Мы рассмотрим два таких метода: метод тяжелого шарика Поляка и ускоренный метод Нестерова. Последний метод является наилучшим из рассмотренных трех и очень популярен в алгоритмах машинного обучения.

Метод тяжелого шарика Поляка

Англоязычное название этого метода: Heavy Ball.

В классическом методе градиентного спуска при очередной итерации точка всегда сдвигается в направлении антиградиента. Как видно на приведенных выше иллюстрациях, это может приводить к осцилляциям, когда мера обусловленности гессиана минимизируемой функции большая и шаг градиентного спуска тоже достаточно большой.

Идея метода тяжелого шарика в том, что мы как бы добавляем инерцию к движению точки. Степень инерции регулируется параметром $\beta$, который обычно в алгоритмах машинного обучения называется моментом (англ. momentum). На очередном шаге алгоритма точка сдвигается на вектор антиградиента, умноженный на длину шага $\alpha$, к которому дополнительно прибавляется вектор сдвига, вычисленный на предыдущем шаге, умноженный на параметр $\beta$. Значение параметра $\beta$ обязательно должно быть меньше единицы (иначе, разогнавшись, мы уже не остановимся); чем больше $\beta$, тем больше инерция влияет на движение точки, которая скатывается в направлении минимума подобно тяжелому шарику. При этом инерция влияет на уменьшение осцилляций в случае плохо обусловленной матрицы гессиана функции $f$ (точка быстрее выходит на большую полуось эллипсоида). Если параметр $\beta$ равен нулю, то метод тяжелого шарика превращается в обычный метод градиентного спуска.

Значение $x_{k+1}$ при очередной итерации в методе тяжелого шарика вычисляется по формуле $$ x_{k+1} = x_k - \alpha \nabla f(x_k) + \beta(x_k - x_{k-1}),\quad k \ge 1, \quad 0 \le \beta < 1. $$ На следующей иллюстрации показаны трактории движения точки при обычном методе градиентного спуска (красная линия) и в методе тяжелого шарика (синяя линия):

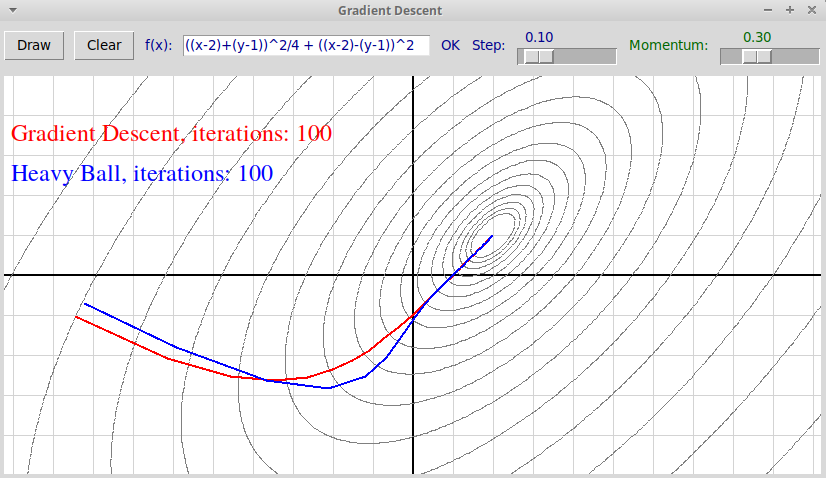
Здесь размер шага $\alpha=0.1$ невелик и осцилляций в методе градиентного спуска не происходит. Увеличив $\alpha = 0.4$, получим такую картинку:

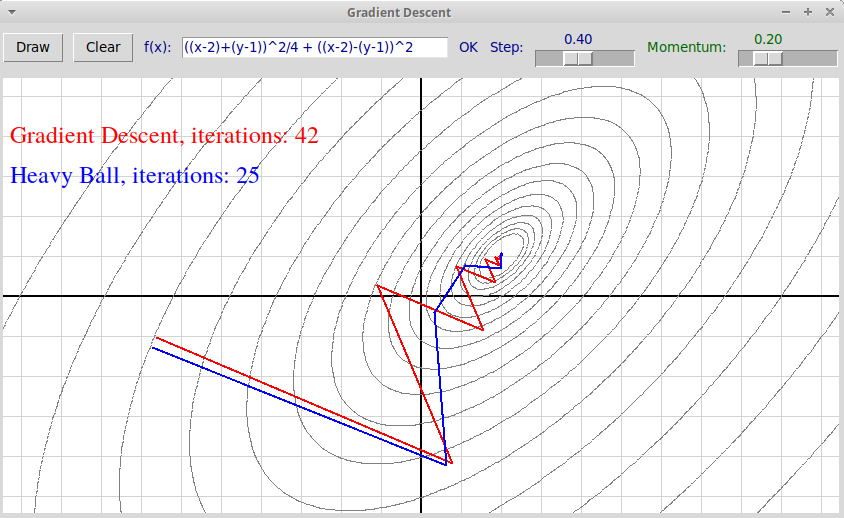
(Мы также уменьшили параметр $\beta = 0.2$.)

На последней иллюстрации видно, что, помимо уменьшения осцилляций, метод тяжелого шарика сходится быстрее: 25 итераций против 42 в простом методе градиентного спуска.

Ускоренный метод градиентного спуска Нестерова

Ускоренный метод Нестерова значительно улучшает сходимость и скорость градиентного спуска, при том, что его программная реализация ничуть не сложнее. В методе Нестерова используется та же идея, что и в методе тяжелого шарика. Различие с методом тяжелого шарика в том, что при очередной итерации антиградиент функции вычисляется не в текущей точке $x_k$, а в точке $y_k$, в которую сдвинулась бы точка $x_k$ с учетом только инерции. Применяются следующие формулы: $$ \begin{array}{l} y_0 = x_0 \\ x_1 = y_0 - \alpha \nabla f(y_0) \\ y_1 = x_1 + \beta (x_1 - x_0) \\ \dots \\ x_{k+1} = y_k - \alpha \nabla f(y_k) \\ y_{k+1} = x_{k+1} + \beta(x_{k+1} - x_k) \end{array} $$ Неформально говоря, мы как бы прогнозируем будущее движение точки, учитывая ее инерцию, и на очередной итерации используем значение антиградиента функции не в текущей, а в прогнозируемой точке. (Аналогия с движением автомобиля: входя в поворот, мы учитываем его кривизну не в самом начале поворота, а в той его точке, куда мы попадем через некоторый промежуток времени.)

Следующий рисунок иллюстрирует метод Нестерова:

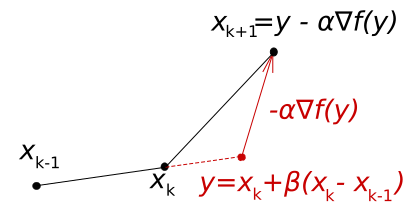
Вот скриншот программы, иллюстрирующей ускоренные методы градиентного спуска. Зеленая траектория соответствует методу Нестерова, синяя — методу тяжелого шарика:

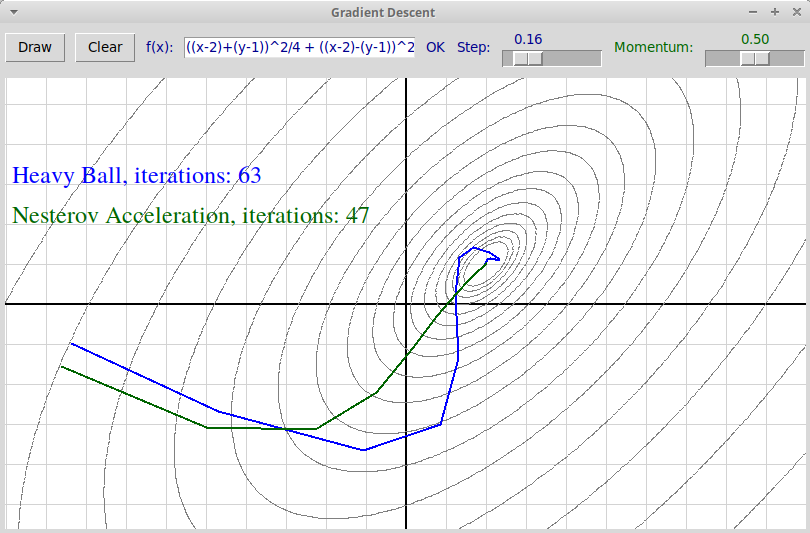
Видно, что в случае метода Нестерова инерция в меньшей степени влияет на отклонение траектории от оптимальной, и при данных параметрах метод Нестерова сходится быстрее.

Сравнение всех трех методов градиентного спуска приведено на следующем скриншоте:
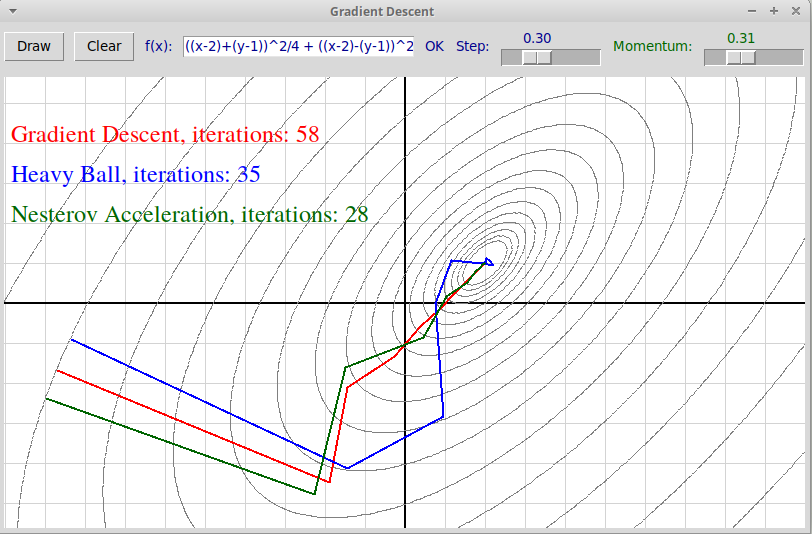
В данном случае метод Нестерова сходится быстрее всех.

Оценка скорости сходимости метода Нестерова

Пусть непрерывно дифференцируемая функция $f(x)$ удовлетворяет условию Липшица для градиента с константой $L$: $$ ||\nabla f(x_1) - \nabla f(x_2)|| \le L ||x_1 - x_2|| $$ Пусть параметры $\alpha$ (размер шага, скорость обучения) и $\beta$ (степень инерции, момент) удовлетворяют неравенствам: $$ 0 \le \beta < 1, \quad 0 \le \alpha < 2(1 - \beta)/L. $$ Тогда методы Тяжелого шарика и Нестерова сходятся.

В методе Нестерова обычно выбирается длина шага $$ \alpha = 1/L. $$ Справедлива следующая оценка на число итераций $N$ для получения точности $\varepsilon$ (т.е. выполнения неравенства $|f(x_N) - f(x_*)| \le \varepsilon$): $$ N = O(LR^2/\sqrt{\varepsilon}). $$ Здесь $R$ — расстояние от точки начального приближения до точки минимума: $R = ||x_0 - x_*||$.

Сравним со скоростью сходимости классического метода градиентного спуска: $$ N = O(LR^2/\varepsilon). $$ Мы видим, что линейная зависимость числа итераций $N$ от величины $1/\varepsilon$, обратной требуемой точности, заменилась на зависимость от квадратного корня из $1/\varepsilon$. То есть при улучшении точности в 100 раз метод градиентного спуска будет работать в 100 раз дольше, а метод Нестерова замедлится только в 10 раз. Причем для сильно выпуклых функций в случае метода Нестерова уже будет справедлива намного более сильная логарифмическая оценка, но мы ее здесь не приводим.