Нелинейный метод опорных векторов: ядровый вариант
Постановка задачи
Пусть, как и в классическом линейном методе опорных векторов, мы имеем $m$ точек в $n$-мерном пространстве $\Bbb{R}^n$: $$ x_1, x_2, \dots, x_m \in \Bbb{R}^n. $$ Точки описывают объекты некоторых классов, координаты точек играют роль признаков (features). Мы рассматриваем объекты, которые могут принадлежать двум классам, и нам надо научиться отделять эти классы друг от друга.
Пусть мы имеем тренировочные данные, на которых выполнена разметка: точки, принадлежащие первому классу, отмечены числом $1$, точки из второго класса — числом $-1$. Соответствующую переменную мы будем обозначать через $y_i$: если пара $(x_i, y_i)$ принадлежит первому классу, то $y_i = 1$, иначе $y_i = -1$.
В классическом методе опорных векторов вычисляется гиперплоскость коразмерности 1, которая разделяет эти два класса: $$ \langle w, x\rangle - b = 0, \quad w\in \Bbb{R}^n, \quad x\in \Bbb{R}^n, \quad b\in \Bbb{R}. $$ Здесь вектор $w$ — это нормаль к гиперплоскости, $x$ — точка гиперплоскости, $b$ — вещественная константа; угловыми скобками обозначено скалярное произведение векторов.
Если для конкретной точки $p\in \Bbb{R}^n$ выполняется неравенство $$ \langle w, p\rangle - b \ge 0, $$ то мы считаем, что точка $p$ принадлежит первому классу; если выражение в левой части меньше нуля, то второму классу. Таким образом, строится линейный классификатор, разделяющий точки двух классов.
Разделимый случай
Далеко не всегда можно построить гиперплоскость, разделяющую два множества.
Но для начала допустим, что это можно сделать: точки первого класса
лежат в верхнем полупространстве, задаваемой некоторой гиперплоскостью,
точки второго класса — в нижнем полупространстве. Допустим также,
что никакие точки не лежат на самой гиперплоскости, т.е. неравенства
на точках $x_i$ строгие. Наилучшее разделение классов достигается тогда,
когда минимальное расстояние от гиперплоскости до точек обоих классов
максимально возможное. Понятно, что в этом случае минимальное расстояние
до точек первого класса равно минимальному расстоянию до точек второго
класса:
Обозначим это минимальное расстояние через $h$.
Точки, находящиеся на расстоянии $h$ до гиперплоскости,
называются опорными (support), отсюда и название этого метода
(support vector machine).
Применим формулу для расстояния со знаком от точки $p$ до плоскости, заданной уравнением $\langle w, x\rangle - b = 0$: $$ h = (\langle w, p\rangle - b)/|w|, $$ где через $|w|$ обозначена длина вектора нормали $w$. Для опорных точек выполняется условие $$ y_i(\langle w, x_i\rangle - b)/|w| = h, $$ (здесь знак в правой части исчезает за счет домножения на $y_i = \pm 1$). Для всех остальных точек выполняется неравенство: $$ y_i(\langle w, x_i\rangle - b)/|w| \ge h. $$ Домножив неравенство на $1/h$, получим: $$ y_i(\langle w, x_i\rangle - b)/(|w|\cdot h) \ge 1. $$ Обозначим теперь $w' = w\cdot(1/(|w|\cdot h))$, $b' = b/(|w|\cdot h)$. От умножения гиперплоскость не изменится, и точки $x_i$ будут удовлетворять неравенству: $$ y_i(\langle w', x_i\rangle - b') \ge 1. $$ При этом, поскольку $w' = w\cdot(1/(|w|\cdot h))$, то $$ \begin{array}{l} |w'| = |w|/(|w|\cdot h)\quad =\gt \\ h = 1/|w'|. \end{array} $$ Отсюда получаем, что ширина полосы, разделяющей два множества, равна $2h = 2/|w'|$. Чтобы не загромождать обозначения, будем снова обозначать неизвестные параметры гиперплоскости через $w$, $b$ (опустим штрихи). Итак, нам надо максимизировать ширину полосы, разделяющей два класса точек, при том, что все точки одного класса лежат в положительном полупространстве, все точки другого — в отрицательном. Ширина полосы обратно пропорциональна длине вектора нормали $|w|$, значит, нам надо минимизировать $|w|$, или, что то же самое, минимизировать квадрат длины $|w|^2$. Мы пришли к следующей постановке задачи условной минимизации: $$ \begin{array}{l} y_i(\langle w, x_i\rangle - b) \ge 1, \quad i=1,2,\dots,m \\ |w|^2 \to \min. \end{array} $$
Эту задачу можно решать методами математического программирования. Тем не менее мы не будем сейчас рассматривать методы ее решения. Отметим, что в общем случае эта задача неразрешима, когда два множества невозможно разделить никакой гиперплоскостью. Рассмотрение этой задачи нам понадобилось только для того, чтобы обосновать более общую постановку задачи, которая уже имеет решение всегда.
Неразделимый случай
В общем случае система неравенств $$ y_i(\langle w, x_i\rangle - b) \ge 1, \quad i=1,2,\dots,m $$ неразрешима, когда два множества невозможно разделить гиперплоскостью. Ослабим немного эти неравенства: введем переменные $\xi_i$ с ограничениями $\xi_i \ge 0$ и разрешим выражениям для расстояния до гиперплоскости быть чуть меньшими, чем 1, на величины $\xi_i$: $$ y_i(\langle w, x_i\rangle - b) \ge 1 - \xi_i, \quad i=1,2,\dots,m $$ Величины $\xi_i$ выражают как бы нашу плату за нахождение ослабленного решения, когда строгого решения не существует. Нам надо минимизировать эту плату, поэтому мы будем минимизировать не только $|w|^2$, но и сумму ослабляющих переменных (в идеальном случае эта сумма должна быть нулевой): $$ |w|^2 + С\cdot 1/m\sum_{i=1}^m \xi_i \to \min. $$ Здесь константа $C$ — гипер-параметр нашего алгоритма. Чем больше $C$, тем большее значение имеет расположение точек в правильной полуплоскости в соответствии с их классом. При меньших значениях параметра $C$ большее значение придается ширине разделяющего слоя между множествами точек двух классов, параллельного гиперплоскости. Отметим, что слагаемое $|w|^2$ можно рассматривать как параметр регуляризации (он имеет тем большее значение, чем меньше $C$).
Итак, теперь наша задача формулируется следующим образом: $$ \begin{array}{l} |w|^2 + C\cdot 1/m\sum_{i=1}^m \xi_i \to \min \\ y_i(\langle w, x_i\rangle - b) \ge 1 - \xi_i, \quad i=1,2,\dots,m \\ \xi_i \ge 0 \end{array} $$
Это задача условной минимизации.
Ранее, рассматривая линейный случай, мы сумели исключить переменные
$\xi_i$ из нашей системы
и получили задачу безусловной оптимизации. Это было сделано следующим
образом:
$$
\begin{array}{l}
\xi_i \ge 1 - y_i(\langle w, x_i\rangle - b) \\
\xi_i \ge 0
\end{array}
$$
Поскольку $\xi_i$ должны быть как можно меньше, но при этом неотрицательные,
то для выполнения этих двух условий достаточно выполнения равенства
$$
\xi_i = \max(1 - y_i(\langle w, x_i\rangle - b), 0).
$$
Теперь, подставив выражение для $\xi_i$ в целевую функцию, получим:
$$
|w|^2 + C\cdot 1/m
\sum_{i=1}^m \max(1 - y_i(\langle w, x_i\rangle - b), 0)
\to \min_{w, b}
$$
В результате мы свели нашу задачу поиска условного экстремума к
безусловной, которую уже можно решить обычными методами минимизации
(градиентный спуск, методы сопряженных градиентов и т.п.).
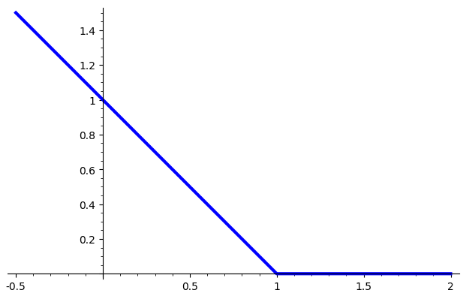
Функция
$$
H(x) = \max(1 - x, 0), \quad x\in \Bbb{R}
$$
носит название Hinge Loss. Вот ее график:
С использованием функции Hinge Loss нашу задачу теперь можно переписать в виде $$ |w|^2 + C\cdot 1/m \sum_{i=1}^m H(y_i(\langle w, x_i\rangle - b)) \to \min_{w, b} $$
Нелинейный вариант метода опорных векторов, использующий расширение исходного набора признаков добавлением к ним некоторого множества базисных функций от этих признаков
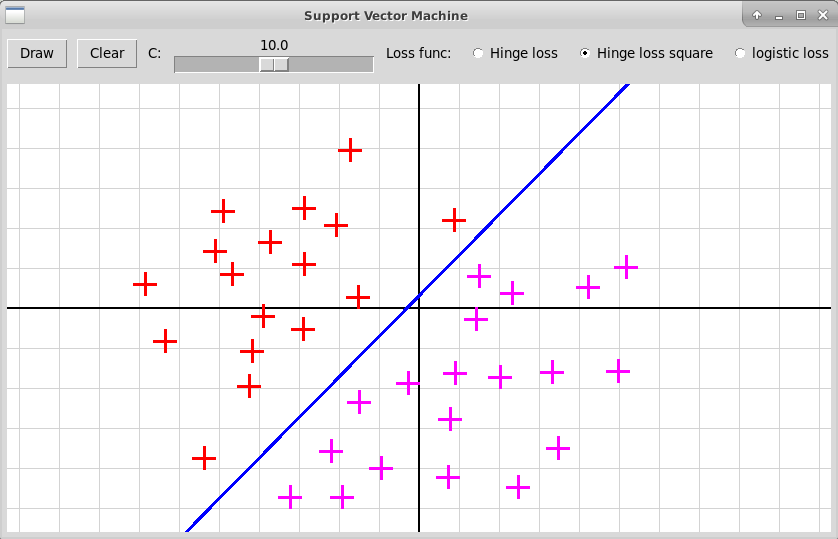
Далеко не всегда можно удовлетворительно разделить точки двух классов гиперплоскостью. В таком случае можно дополнить набор признаков объектов, т.е. координаты представляющих их векторов $n$-мерного пространства, какими-либо базовыми функциями от этих векторов. Например, можно рассмотреть всевозможные произведения (мономы) степени не выше $d$ от координат векторов. Мы строим нелинейное отображение $$ % \begin{array}{l} \begin{array}{l} \varphi(x): \Bbb{R}^n \to \Bbb{R}^m, \quad m > n, \\ \varphi(x) = (\varphi_1(x), \varphi_2(x), \dots, \varphi_m(x)), \end{array} % \end(array} $$ которое переводит исходный набор признаков объекта $x = (x_1, x_2, \dots, x_n)$ в расширенный набор признаков $(\varphi_1(x), \varphi_2(x), \dots, \varphi_m(x))$. Пусть нам удалось построить хороший линейный классификатор $F(t)$ в пространстве расширенных признаков: $$ F(t) = \langle W, t \rangle - B, \quad \text{где}\ W, t\in \Bbb{R}^m,\ % B \in \Bbb{R}. $$ Тогда классификатор в исходном пространстве (уже нелинейный!) задается формулой $$ f(x) = F(\varphi(x)) = \langle W, \varphi(x)\rangle - B. $$
В простейшем случае в качестве функций
$\varphi_1(x_1, \dots, x_n)$,
$\varphi_2(x_1, \dots, x_n)$,
$\dots$,
$\varphi_m(x_1, \dots, x_n)$,
можно взять всевозможные мономы степени не выше $d$ от
переменных
$x_1, x_2, \dots, x_n$
(то есть от исходных признаков).
Пусть, например, $d = 2$. Пусть число исходных признаков $n = 2$,
т.е. объекты представляются точками плоскости $\Bbb{R}^2$.
Тогда расширенный набор признаков представляется всеми мономами
степени не выше 2 от переменных $x_1$, $x_2$:
$$
\varphi(x_1, x_2) = (x_1, x_2, x_1^2, x_1 x_2, x_2^2),
$$
и размерность пространства расширенных признаков $m=5$.
Ниже приведен скриншот программы, применяющей этот метод для
разделения двух классов точек нелинейным методом опорных векторов:
Теорема Куна–Таккера и двойственная задача
Недостатком рассмотренного выше метода построения нелинейного классификатора является увеличение размерности пространства, в котором мы строим линейный классификатор, и, таким образом, существенное замедление вычислений. Если, например, мы рассматриваем все мономы степени не выше 3 от координат объектов, которые представляются точками $n$-мерного пространства, то размерность расширенного пространства будет равна $O(n^3)$. Но, оказывается, можно построить нелинейный классификатор, который по сути работает в пространстве более высокой размерности, не увеличивая сложности вычислений. Этот метод основан на использовании понятия ядра, которое является обобщением скалярного произведения в $n$-мерном пространстве.
Вернемся еще раз к нашей задачи построения линейного классификатора (гиперплоскости в $n$-мерном пространстве) в линейно неразделимом случае. Искомая гиперплоскость находится как решение оптимизационной задачи: $$ \begin{array}{l} |w|^2 + C\cdot 1/m\sum_{i=1}^m \xi_i \to \min \\ y_i(\langle w, x_i\rangle - b) \ge 1 - \xi_i, \quad i=1,2,\dots,m \\ \xi_i \ge 0 \end{array} $$
Для удобства преобразований формул немного переформулируем ее:
1) опустим усредняющий множитель $1/m$;
2) добавим множитель $1/2$ перед $|w|^2$.
Получим:
$$
\begin{array}{l}
|w|^2/2 + C\cdot \sum_{i=1}^m \xi_i \to \min \\
y_i(\langle w, x_i\rangle - b) \ge 1 - \xi_i, \quad i=1,2,\dots,m \\
\xi_i \ge 0
\end{array}
$$
Теперь перепишем условия так, чтобы можно было применить теорему Каруша–Куна–Таккера: $$ \begin{array}{l} |w|^2/2 + C\cdot \sum_{i=1}^m \xi_i \to \min \\ y_i(\langle w, x_i\rangle - b) + \xi_i - 1 \ge 0, \quad i=1,2,\dots,m \\ \xi_i \ge 0 \end{array} $$
Теорема Каруша–Куна–Таккера
Напомним теорему Каруша–Куна–Таккера. Она обобщает теорему Лагранжа об условном экстремуме функции. В теореме Лагранжа мы ищем максимум или минимум функции $f(x)$ при выполнении одного или нескольких условий в виде равенств нулю функций $h_i(x)$, $i=1,\dots,k$: $$ \begin{array}{l} f: \Bbb{R}^n \to \Bbb{R}, \\ f(x) \to \min \quad \text{при условиях}\\ h_i(x) = 0, \quad i=1,\dots,k. \end{array} $$ В теореме Лагранжа мы вводим дополнительные множители $\lambda_1, \lambda_2,\dots,\lambda_k\in\Bbb{R}$ и выписываем лагранжиан для задачи поиска экстремума: $$ L(x, \lambda_1,\dots, \lambda_k) = f(x) + \sum_{i=1}^k \lambda_i h_i(x). $$ Теорема Лагранжа дает необходимое условие того, что точка $\bar{x}$ является точкой условного локального экстремума для функции f(x): найдутся такие множители $\bar\lambda_1, \bar\lambda_2,\dots,\bar\lambda_k\in\Bbb{R}$, что точка $(\bar{x}, \bar\lambda_1,\dots,\bar\lambda_k)$ является точкой (безусловного) экстремума для лагранжиана, т.е. градиент лагранжиана в этой точке равен нулю: $$ \nabla L(\bar{x}, \bar\lambda_1,\dots,\bar\lambda_k) = 0. $$
Теорема Каруша–Куна–Таккера обобщает теорему Лагранжа на случай, когда мы имеем ограничения не только в виде равенств, но также и в виде неравенств: $$ \begin{array}{l} f(x) \to \min \quad \text{при условиях}\\ g_i(x) \le 0, \quad i=1,\dots,m,\\ h_j(x) = 0, \quad j=1,\dots,k. \end{array} $$ Выписываем лагранжиан для задачи условной минимизации, вводя дополнительные множители $\lambda_1, \lambda_2,\dots,\lambda_m\in\Bbb{R}$, $\lambda_i\ge 0$ и $\mu_1, \mu_2,\dots,\mu_k\in\Bbb{R}$: $$ \begin{array}{l} L(x, \lambda_1,\dots,\lambda_m, \mu_1,\dots,\mu_k) = f(x) + \sum_{i=1}^m \lambda_i g_i(x) + \sum_{j=1}^k \mu_j h_j(x), \\ \lambda_i \ge 0, \quad i=1,\dots,m. \end{array} $$ Пусть $\bar{x}$ — точка условного локального минимума функции $f(x)$. Тогда теорема Куна-Таккера утверждает, что найдутся такие значения множителей $\bar\lambda =(\bar\lambda_1,\dots,\bar\lambda_m)$ и $\bar\mu=(\bar\mu_1,\dots,\bar\mu_k)$, что точка $(\bar{x},\bar{\lambda},\bar{\mu})$ является седловой точкой для функции лагранжиана: точкой минимума по переменной $x$ и точкой максимума по переменным $\lambda_i$.
Выполняются следующие необходимые условия в точке условного минимума $\bar{x}$: $$ \begin{array}{l} \nabla_x L(\bar{x}, \bar\lambda, \bar\mu) = 0, \\ \bar\lambda_i \ge 0, \quad i=1,\dots,m, \\ \bar\lambda_i g_i(\bar{x}) = 0, \quad i=1,\dots,m \quad \text{(условия дополняющей нежесткости)}. \end{array} $$
Применение теоремы Каруша–Куна–Таккера в методе опорных векторов
Вернемся к нашей задаче классификации в методе опорных векторов. Мы свели ее к следующей задаче условной минимизации: $$ \begin{array}{l} |w|^2/2 + C\cdot \sum_{i=1}^m \xi_i \to \min \\ y_i(\langle w, x_i\rangle - b) + \xi_i - 1 \ge 0, \quad i=1,2,\dots,m \\ \xi_i \ge 0. \end{array} $$ Отметим, что у нас есть только условия в виде неравенств. В соответствии с теоремой Каруша–Куна–Таккера введем дополнительные множители $\lambda=(\lambda_1,\dots,\lambda_m)$ и $\mu=(\mu_1,\dots,\mu_m)$, $\lambda_i, \mu_i \ge 0$, и выпишем лагранжиан задачи условной минимизации: $$ L(w, b, \xi, \lambda, \mu) = |w|^2/2 + C\cdot \sum_{i=1}^m \xi_i - \sum_{i=1}^m \lambda_i(y_i(\langle w, x_i\rangle - b) + \xi_i - 1) - \sum_{i=1}^m \mu_i\xi_i $$ (минус перед суммой стоит потому, что в теореме Куна–Таккера используются неравенства $\le 0$, а в нашем случае неравенства имеют противоположный знак).
Выпишем теперь необходимые условия условного минимума из теоремы Каруша–Куна–Таккера в нашем случае: $$ \begin{array}{l} \nabla_w L(w, b, \xi, \lambda, \mu) = w - \sum_{i=1}^m \lambda_i y_i x_i = 0 \quad \Rightarrow \\ w = \sum_{i=1}^m \lambda_i y_i x_i. \end{array} $$ Мы получили выражение вектора нормали к гиперплоскости $w$ через векторы $x_i$ и коэффициенты $\lambda_i$. Далее, $$ \frac{\partial}{\partial b} L(w, b, \xi, \lambda, \mu) = \sum_{i=1}^m \lambda_i y_i = 0, $$ а также $$ \frac{\partial}{\partial \xi_i} L(w, b, \xi, \lambda, \mu) = C - \lambda_i - \mu_i = 0, \quad i=1,\dots,m \quad \Rightarrow \\ C = \lambda_i + \mu_i. $$ Условия дополняющей нежесткости записываются в виде $$ \begin{array}{l} \lambda_i(y_i(\langle w, x_i\rangle - b) + \xi_i - 1) = 0, \quad i=1,\dots,m. \end{array} $$ Отсюда вытекает, что $$ \begin{array}{l} \lambda_i = 0 \quad \text{или}\\ y_i(\langle w, x_i\rangle - b) = 1 - \xi_i. \end{array} $$ Наконец, из условий дополняющей нежесткости для $\xi_i$ вытекает, что $$ \begin{array}{l} \mu_i\xi_i = 0 \quad \Rightarrow \\ \mu_i = 0 \ \text{или}\ \xi_i = 0. \end{array} $$
Подставим выражение $w = \sum_{i=1}^m \lambda_i y_i x_i$ в лагранжиан. Учитывая также условия $\sum_{i=1}^m \lambda_i y_i = 0$ и $С - \lambda_i - \mu_i = 0$, получим: $$ \begin{array}{l} L(w, b, \xi, \lambda, \mu) = \langle w, w\rangle/2 + C\cdot \sum_{i=1}^m \xi_i - \sum_{i=1}^m \lambda_i(y_i(\langle w, x_i\rangle - b) + \xi_i - 1) - \sum_{i=1}^m \mu_i\xi_i = \\ = \frac{1}{2} \langle \sum_i \lambda_i y_i x_i, \sum_j \lambda_j y_j x_j \rangle + C \sum_i \xi_i - \sum_i\lambda_i(y_i(\langle \sum_j\lambda_j y_j x_j, x_i\rangle - b) + \xi_i - 1) - \sum_i\mu_i\xi_i = \\ = \frac{1}{2}\sum_i\sum_j \lambda_i\lambda_j y_i y_j \langle x_i, x_j \rangle + C \sum_i \xi_i - \sum_i\sum_j \lambda_i\lambda_j y_i y_j \langle x_i, x_j \rangle\\ \qquad + \sum_i \lambda_i y_i b - \sum_i \lambda_i\xi_i + \sum_i \lambda_i - \sum_i\mu_i\xi_i = \\ = -\frac{1}{2}\sum_i\sum_j \lambda_i\lambda_j y_i y_j \langle x_i, x_j \rangle + \sum_i (C - \lambda_i - \mu_i)\xi_i + \sum_i \lambda_i = \\ = \sum_i \lambda_i - \frac{1}{2}\sum_i\sum_j \lambda_i\lambda_j y_i y_j \langle x_i, x_j \rangle \end{array} $$ Итак, мы получили окончательную формулу для лагранжиана: $$ L = \sum_{i=1}^m \lambda_i - \frac{1}{2}\sum_{i=1}^m \sum_{j=1}^m \lambda_i\lambda_j y_i y_j \langle x_i, x_j \rangle. $$ Мы получили, что лагранжиан не зависит от исходных переменных $w, b, \xi_i$, а зависит только от двойственных переменных $\lambda_i$, причем в его выражение входят только попарные скалярные произведения векторов $x_i, x_j$. Значения переменных $\lambda_i$ находятся путем решения двойственной задачи: $$ \begin{array}{l} \sum_{i=1}^m \lambda_i - \frac{1}{2}\sum_{i,j=1}^m \lambda_i\lambda_j y_i y_j \langle x_i, x_j \rangle \to \max_\lambda \\ \text{при ограничениях} \\ \sum_{i=1}^m \lambda_i y_i = 0, \\ 0 \le \lambda_i \le C. \end{array} $$
Решив двойственную задачу, мы можем вычислить вектор нормали $w$ к гиперплоскости по формуле $$ w = \sum_{i=1}^m \lambda_i y_i x_i. $$ Чуть сложнее вычислить свободный член $b$, задающий смещение гиперплоскости относительно начала координат. Для этого найдем индекс $i$ такой, что $0 < \lambda_i < C$ (неравенства строгие!). Из того, что $С = \lambda_i + \mu_i$, $\lambda_i, \mu_i\ge 0$, следует, что $\mu_i \ne 0$; поэтому из условия дополняющей нежесткости $\mu_i \xi_i = 0$ следует, что $\xi_i = 0$. Поскольку $\lambda_i \ne 0$, то из другого условия дополняющей нежесткости $$ \lambda_i(y_i(\langle w, x_i\rangle - b) + \xi_i - 1) = 0, $$ вытекает, что $$ y_i(\langle w, x_i\rangle - b) = 1. $$ Такие объекты $x_i$ называются опорными граничными, они лежат в точности на границе полосы, разделяющей два класса объектов. Подобные объекты всегда существуют (иначе разделяющую полосу можно было бы расширить).
Итак, найдем множитель $\lambda_i$, для которого $0 < \lambda_i < C$. Такой множитель обязательно найдется. Тогда для объекта $x_i$ выполняется равенство $$ y_i(\langle w, x_i\rangle - b) = 1, $$ из которого, учитывая, что $y_i = \pm 1$, находим $b$: $$ b = \langle w, x_i\rangle - y_i. $$
Использование ядра в нелинейном методе опорных векторов
Итак, мы свели нашу задачу условной минимизации к двойственной задаче нахождения максимума лагранжиана по переменным $\lambda_i$: $$ \begin{array}{l} \sum_{i=1}^m \lambda_i - \frac{1}{2}\sum_{i,j=1}^m \lambda_i\lambda_j y_i y_j \langle x_i, x_j \rangle \to \max_\lambda \\ \text{при ограничениях} \\ \sum_{i=1}^m \lambda_i y_i = 0, \\ 0 \le \lambda_i \le C. \end{array} $$ Функция, которую надо максимизировать, зависит только от попарных скалярных произведений $\langle x_i, x_j \rangle$ векторов $x_i$, представляющих наши объекты. Возьмем теперь вместо скалярных в исходном пространстве функцию ядра $K(x_i, x_j)$, которая соответствует скалярному произведению образов векторов $x_i, x_j$ в некотором пространстве более высокой размерности, возможно, даже бесконечномерном. Это пространство называют спрямляющим. Для образов векторов вероятность, что найдется гиперплоскость в спрямляющем пространстве, линейно их разделяющая, гораздо выше. Решим двойственную задачу, использовав вместо скалярных произведений значение ядра: $$ \begin{array}{l} \sum_{i=1}^m \lambda_i - \frac{1}{2} \sum_{i,j=1}^m \lambda_i\lambda_j y_i y_j K(x_i, x_j) \to \max_\lambda \\ \text{при ограничениях} \\ \sum_{i=1}^m \lambda_i y_i = 0, \\ 0 \le \lambda_i \le C. \end{array} $$ Найдя эту гиперплоскость, заданную параметрами $w, b$, мы построим нелинейный классификатор $$ f(x) = K(w, x) - b, $$ который относит объект $x$ к первому классу, если $f(x) > 0$, и ко второму, если $f(x) < 0$.
Какие бывают ядра
Самым популярным является гауссовское ядро, оно обычно обозначается аббревиатурой RBF (Radial Basis Function): $$ K(x, x') = \exp(- \frac{||x - x'||^2}{2\sigma^2}) $$ Спрямляющее пространство здесь бесконечномерно.
Также довольно часто используют полиномиальное ядро степени $d$: $$ K(x, x') = (\langle x, x'\rangle + c)^d, $$ где $c\in\Bbb{R},\ c\ge0$ — параметр, который определяет влияние на результат мономов высоких и низких степеней.
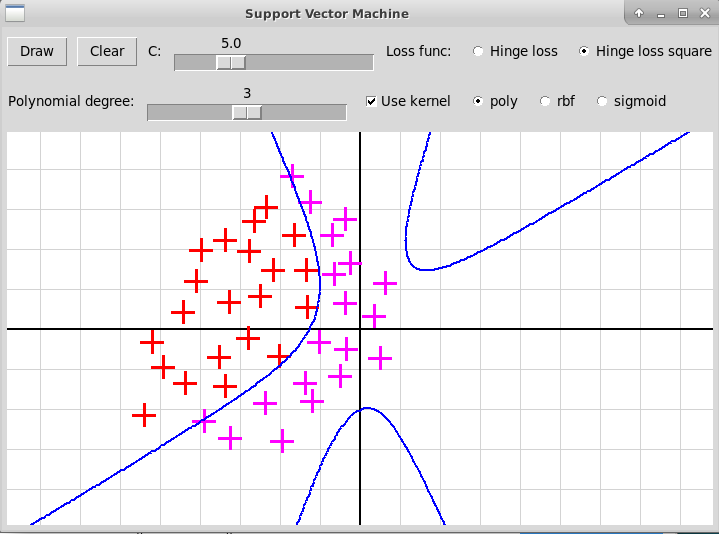
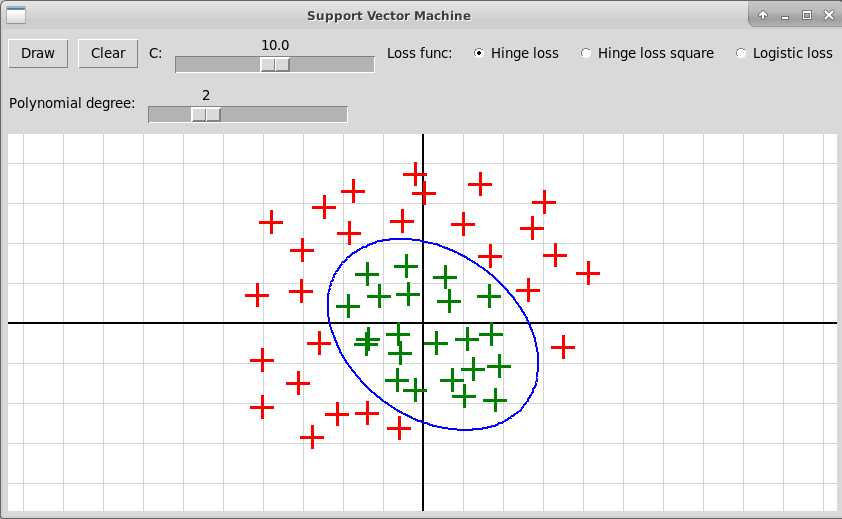
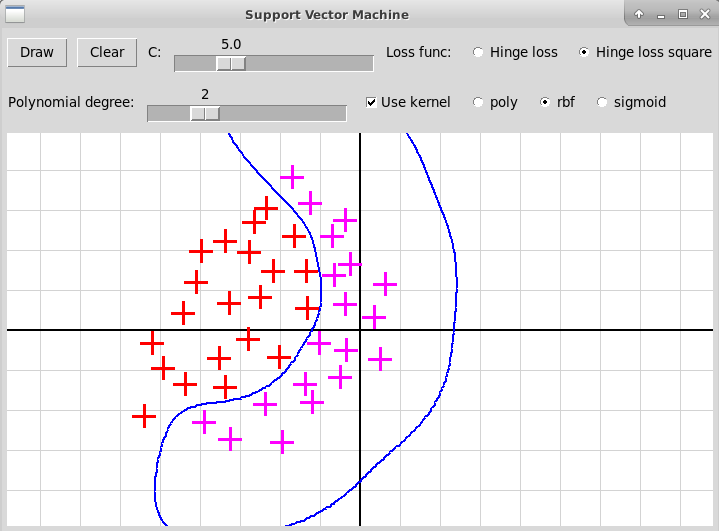
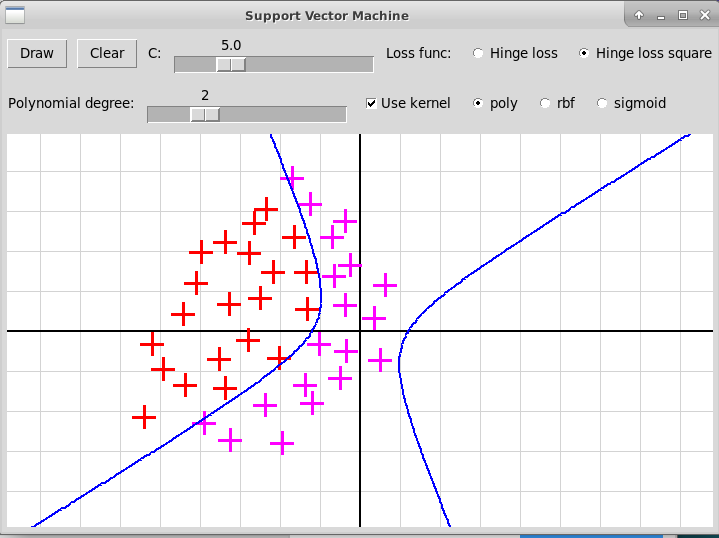
Вот скриншоты оконной программы, иллюстрирующей
ядровый метод опорных векторов для гауссовского и полиномиального
ядер:
Гауссовское ядро (RBF)
Полиномиальное ядро, степень 2
Полиномиальное ядро, степень 3