Линейная регрессия и ее решение методом наименьших квадратов

Пусть нам нужно найти зависимость между двумя величинами: независимой величиной $x$ и зависящей от нее величиной $y$. Пусть нам априори известно, что зависимость, например, линейная, или квадратичная, или в общем случае задается многочленом некоторой заранее известной степени $n$: $$ y = w_0 x^n + w_1 x^{n-1} + \dots + w_{n-1} x + w_n. $$ Требуется определить коэффициенты $w_i$ этого многочлена. Обозначим многочлен через $f(x)$: $$ f(x) = w_0 x^n + w_1 x^{n-1} + \dots + w_{n-1} x + w_n. $$

Мы можем измерить значения зависимой величины $y$ для некоторого набора значений независимой величины $x$: $$ y_i = y(x_i),\quad i = 1, 2,\dots, m. $$ Если бы измерения были точными, то нам хватило бы $n+1$-го измерения, чтобы точно вычислить все коэфиициенты $w_i$ искомого многочлена $p(x)$. Однако на практике измерения выполняются с некоторой погрешностью: $$ y_i = f(x_i) + \xi_i, $$ где $\xi_i$ представляет собой ошибку $i$-го измерения. Мы предполагаем, что при различных измерениях ошибки независимы, причем они представляют собой случайную величину, распределенную по нормальному закону с нулевым матожиданием и одной и той же дисперсией. Поэтому $n+1$-го измерения не достаточно, скорее всего, коэффициенты многочлена $f$ будут вычислены с ошибкой. Поэтому надо выполнить большее число измерений — количество $m$ измерений должно быть больше, чем число коэффициентов многочлена $n+1$. Но тогда система уравнений $$ \begin{array}{l} y_1 = f(x_1)\\ y_2 = f(x_2)\\ \dots \\ y_m = f(x_m) \end{array} $$ где неизвестными являются коэффициенты $w_0, w_1,\dots,w_n$ многочлена $f(x)$, в общем случае не имеет точного решения.

В методе наименьших квадратов используется принцип максимального правдоподобия — коэффициенты $w_j$ многочлена $f$ подбираются так, чтобы вероятность получения данного набора измерений $y_i$ была бы максимальной. Поскольку для нормального распределения плотность вероятности обратно пропорциональна квадрату отклонения от среднего значения, следует выбрать коэффициенты многочлена так, чтобы минимизировать сумму квадратов отклонений измерений $y_i$ от значений многочлена $f$ в соответствующих точках $x_i$: $$ \sum_{i=1}^m (y_i - f(x_i))^2\ \to \min. $$

Запишем систему уравнений в виде линейной системы, используя коэффициенты многочлена $f$: $$ \begin{array}{l} y_1 = w_0 x_1^n + w_1 x_1^{n-1} + \dots + w_{n-1} x_1 + w_n \\ y_2 = w_0 x_2^n + w_1 x_2^{n-1} + \dots + w_{n-1} x_2 + w_n \\ \dots \\ y_m = w_0 x_m^n + w_1 x_m^{n-1} + \dots + w_{n-1} x_m + w_n \\ \end{array} $$ Неизестными в этой системе являются коэффициенты $w_0, w_1,\dots. w_n$. Поскольку число неизвестных $n+1$ меньше, чем число уравнений $m$, то система в общем случае не имеет точного решения.

Обозначим через $A$ матрицу системы: $$ A = \begin{array}{|lllll|} \ x_1^n & x_1^{n-1} & \dots & x_1 & 1 \ \\ \ x_2^n & x_2^{n-1} & \dots & x_2 & 1 \ \\ \ & \dots \\ \ x_m^n & x_m^{n-1} & \dots & x_m & 1 \ % \end{array} $$ Это матрица Вандермонда, при различных $x_i$ ее столбцы линейно независимы. Обозначим через $W$ столбец переменных $w_j$, $j=0, 1, \dots, n$, через $Y$ — столбец измеренных значений зависимой величины $y_i$, $i=1, 2, \dots, m$. В матричном виде система уравнений записывается как $$ AW = Y. $$ Здесь $W\in \Bbb{R}^{n+1}$, $Y\in \Bbb{R}^m$, матрицу $A$ можно рассматривать как линейный оператор $A: \Bbb{R}^{n+1} \to \Bbb{R}^{m}$, где $m > n+1$.

В методе наименьших квадратов надо найти такое значение $V$ вектора $W$, при котором евклидово расстояние между векторами $AV$ и $Y$ минимально: $$ ||AV - Y|| \to \min. $$ Это означает, что разность векторов $AV - Y$ перпендикулярна образу $AW$ линейного оператора $A$ (это линейное подпространство в $\Bbb{R}^m$); иначе говоря, вектор $AV$ является ортогональной проекцией вектора $Y$ на подпространство $AW$, где $W$ пробегает все пространство $\Bbb{R}^{n+1}$. Это условие записывается как равенство нулю скалярного произведения вектора $AV - Y$ на любой вектор вида $AW$. В матричном виде: $$ (AV - Y)^T \cdot AW = 0 $$ (верхний индекс $T$ обозначает транспонирование матрицы). Поскольку это равенство выполняется для любого вектора $W$, то имеем матричное равенство $$ (AV - Y)^T \cdot A = 0 $$ или $$ (AV)^T \cdot A = Y^T A. $$ Транспонируем матрицы в обеих частях равенства, чтобы получить более удобное выражение: $$ A^T AV = A^T Y. $$ Это уравнение относительно вектора $V$ называется нормальным уравнением.

Известно, что, если столбцы прямоугольной матрицы $A$ линейно независимы, то произведение $A^T A$ является невырожденной квадратной матрицей. Поэтому матрица $A^T A$ обратима, и искомый вектор $V$ вычисляется как $$ V = (A^T A)^{-1} A^T Y. $$ Вычисленный таким образом вектор $V$ представляет собой решение задачи линейной регрессии методом наименьших квадратов.

Матрица $$ \text{pinv}(A) = (A^T A)^{-1} A^T $$ называется псевдообратной матрицей к матрице $A$ (ее также называют псевдообратной матрицей Мура-Пенроуза). Более точно, это лишь одно из определений псевдообратной матрицы в частном случае, когда $A$ — прямоугольная матрица размера $m\times n$, где $m\ge n$ и столбцы матрицы $A$ линейно независимы.

В общем случае псевдообратная матрица к матрице $A$ вычисляется через сингулярное разложение: $$ A = U S V, $$ где $U$ и $V$ — ортогональные матрицы, а $S$ — диагональная матрица. Точнее, пусть $A$ — прямоугольная матрица размера $m\times n$, тогда $U$ — квадратная ортогональная матрица размера $m\times m$, $S$ — прямоугольная диагональная матрица размера $m\times n$, $V$ — квадратная ортогональная матрица размера $n\times n$: $$ U^T U = \Bbb{1}_m, \quad V^T V = \Bbb{1}_n, \quad S_{ij} = 0\ \text{при}\ i\ne j. $$ Тогда псевдообратная матрица равна $$ \text{pinv}(A) = V^T \cdot S^{-1} U^T, $$ где диагональная матрица $S^{-1}$ получается из матрицы $S$ транспонированием и заменой ненулевых диагональных элементов на обратные к ним.

Пример

Пусть нам известно, что зависимость между величинами $y$ и $x$ кубическая: $$ y = f(x) = w_0 x^3 + w_1 x^2 + w_2 x + w_3 $$ Требуется определить коэффициенты $w_i$ кубического многочлена. Пусть мы измерили значения $y$ в 8 точках $$ x = -3, -2, -1, 0, 1, 2, 3, 4 $$ и получили следующие значения зависимой величины: $$ y = 3, 2, -1, -1, 1, 2, 2, 0. $$ Мы решаем методом наименьших квадратов систему $$ AW = Y $$ где $W = (w0, w1, w2, w3)^T$ — вектор-столбец неизвестных размера 4, $Y$ — вектор-столбец значений зависимой величины $y$ длины 8, $A$ — матрица Вандермонда размера $8\times 4$, построенная по значениям независимой величины $x$: $$ A = \begin{array}{|cccc|} \ -27 & 9 & -3 & 1\ \\ -8 & 4 & -2 & 1\ \\ -1 & 1 & -1 & 1\ \\ 0 & 0 & 0 & 1\ \\ 1 & 1 & 1 & 1\ \\ 8 & 4 & 2 & 1\ \\ 27 & 9 & 3 & 1\ \\ 64 & 16 & 4 & 1\ % \end{array} $$

Для решения системы вычисляется псевдообратная матрица к матрице $A$: $$ \text{pinv}(A) = (A^T A)^{-1} A^T $$ Мы получаем матрицу $$ \text{pinv}(A) = \begin{array}{|rrrrrrrr|} -0.0177 & 0.0126 & 0.0177 &0.00758 &-0.00758 &-0.0177 & -0.0126 & 0.0177 \ \\ 0.0682 &-0.0130 &-0.0444 &-0.0411 & -0.0184 &0.00866 & 0.0249 & 0.0152 \ \\ 0.0253 & -0.173 & -0.168 &-0.0465 & 0.106 & 0.204 & 0.161 & -0.109 \ \\ -0.121 & 0.182 & 0.312 & 0.314 & 0.234 & 0.117 & 0.00866 & -0.0455 \ % \end{array} $$ Умножив на нее вектор-столбец $Y$ измеренных значений зависимой величины $y$, получим решение нашей задачи: $$ \text{pinv}(A)\cdot Y = (-0.121, 0.313, 0.780, -0.141)^T $$ Таким образом, зависимость между $y$ и $x$ задается кубическим многочленом: $$ y = -0.121 x^3 + 0.313 x^2 + 0.780 x - 0.141. 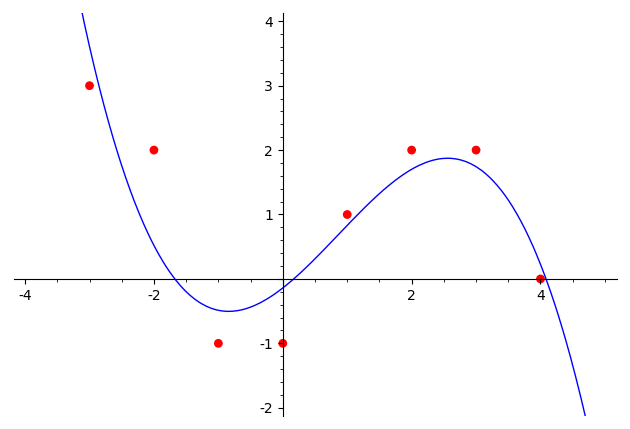$$ Ниже изображены точки $(x_i, y_i)$, соответствующие измерениям величин $x, y$, и график построенного кубического многочлена:

Решение задачи линейной регрессии на языке Python

На языке Python для решения задачи линейной регрессии методом наименьших квадратов следует использовать модуль numpy и его подмодуль numpy.linalg. Матрица создаеся как numpy.array, аналогично представляется вектор-столбец значений зависимой случайной величины $y$. В модуле numpy есть функция numpy.vander для создания матрицы Вандермонда (в общем случае прямоугольной). Функция numpy.linalg.pinv вычисляет псевдообратную матрицу. Вот как реализуется нахождение коэффициентов многочлена степени deg, аппроксимирующего данное множество измерений зависимой величины $y$ при заданных значениях независимой величины $x$.

import numpy as np

def leastSquares(x, y, deg=1):
    '''Compute the coefficients of a polynomial of degree deg
    that approximate the dependence y = y(x) by using the
    Least Squares method.
    Input: x is an array of values of independent variable;
           y is an array of measured values of dependent variable y=y(x);
           deg is the degree of the approximating polynomial.
    Return: the coefficients of the approximating polynomial
            in descending order.'''

    assert len(y) == len(x)

    a = np.vander(x, deg + 1)
    pinv_a = np.linalg.pinv(a)
    w = pinv_a.dot(y)
    return w

Проверим функцию на тех же данных, которые мы использовали в разобранном примере, используя интерпретатор Python'а:

>>> import numpy as np
>>> from leastSquares import *
>>> x = np.array([-3,-2,-1,0,1,2,3,4], dtype="double")
>>> y = np.array([3,2,-1,-1,1,2,2,0], dtype="double")
>>> w = leastSquares(x, y, 3)
>>> w
>>> array([-0.12121212,  0.31277056,  0.78030303, -0.14069264])

Отметим, что в модуле numpy имеется также удобная функция для вычисления значения многочлена, заданного массивом его коэффициентов по убыванию степеней, в точке или в массиве точек: numpy.polyval. Например, вычислим значение многочлена $$ f(x) = x^3 - x - 1 $$ сначала в точке $x = 2$, затем в массиве точек $[0, 1, 2, 3, 4, 5]$. Коэффициенты многочлена $f$ задаются массивом $[1, 0, -1, -1]$ по убыванию степеней:

>>> np.polyval([1, 0, -1, -1], 2)
5
>>> np.polyval([1, 0, -1, -1], [0, 1, 2, 3, 4, 5])
array([ -1,  -1,   5,  23,  59, 119])

Эту функцию удобно использовать для рисования графика многочлена при визуализации данных. Используем библиотеку matplotlib и подмодуль matplotlib.pyplot. Реализуем функцию showLeastSquares в том же файле "leastSquares.py":

import matplotlib.pyplot as plt

def showLeastSquares(x, y, deg=1):
    fig = plt.figure()
    fig.set_size_inches(10/2.54, 10/2.54)
    fig.set_dpi(100)
    ax = fig.add_subplot(1, 1, 1)
    ax.set_aspect(1.)
    xmin = -5
    xmax = 5
    ax.set_xlim(xmin, xmax)
    ax.set_ylim(xmin, xmax)
    ax.grid()
    ax.axhline(0, color="black")
    ax.axvline(0, color="black")

    ax.plot(x, y, "ro")

    w = leastSquares(x, y, deg)

    n = 100; dx = (xmax - xmin)/n
    xx = [ xmin + i*dx for i in range(n+1) ]
    yy = np.polyval(w, xx)
    ax.plot(xx, yy)
    plt.show()

>>> from leastSquares import *
>>> x = [-3,-2,-1,0,1,2,3,4]
>>> y = [3,2,-1,-1,1,2,2,0]
>>> showLeastSquares(x, y, 3)