Метод опорных векторов

Постановка задачи

Пусть мы имеем $m$ точек в $n$-мерном пространстве $\Bbb{R}^n$: $$ x_1, x_2, \dots, x_m \in \Bbb{R}^n. $$ Точки описывают объекты некоторых классов, координаты точек играют роль признаков (features). Нужно построить процедуру, которая позволяет отнести точки к определенному классу. Мы рассматриваем точки, которые могут принадлежать двум классам, и нам надо научиться отделять эти классы друг от друга.

Пусть мы имеем тренировочные данные, на которых выполнена разметка: точки, принадлежащие первому классу, отмечены числом $1$, точки из второго класса — числом $-1$. Соответствующую переменную мы будем обозначать через $y_i$: если пара $(x_i, y_i)$ принадлежит первому классу, то $y_i = 1$, иначе $y_i = -1$.

Наша цель — вычислить гиперплоскость коразмерности 1, которая разделяет эти два класса: $$ \langle w, x\rangle - b = 0, \quad w\in \Bbb{R}^n, \quad x\in \Bbb{R}^n, \quad b\in \Bbb{R}. $$ Здесь вектор $w$ — это нормаль к гиперплоскости, $x$ — точка гиперплоскости, $b$ — вещественная константа; угловыми скобками обозначено скалярное произведение векторов.

Если для конкретной точки $p\in \Bbb{R}^n$ выполняется неравенство $$ \langle w, p\rangle - b \ge 0, $$ то мы считаем, что точка $p$ принадлежит первому классу; если выражение в левой части меньше нуля, то второму классу. Таким образом, наша цель — построить линейный классификатор, который задается вектором $w\in \Bbb{R}^n$ и числом $b\in \Bbb{R}$.

Разделимый случай

Далеко не всегда можно построить гиперплоскость, разделяющую два множества. Но для начала допустим, что это можно сделать: точки первого класса лежат в верхнем полупространстве, задаваемой некоторой гиперплоскостью, точки второго класса — в нижнем полупространстве. Допустим также, что никакие точки не лежат на самой гиперплоскости, т.е. неравенства на точках $x_i$ строгие. Наилучшее разделение классов достигается тогда, когда минимальное расстояние от гиперплоскости до точек обоих классов максимально возможное. Понятно, что в этом случае минимальное расстояние до точек первого класса равно минимальному расстоянию до точек второго класса:

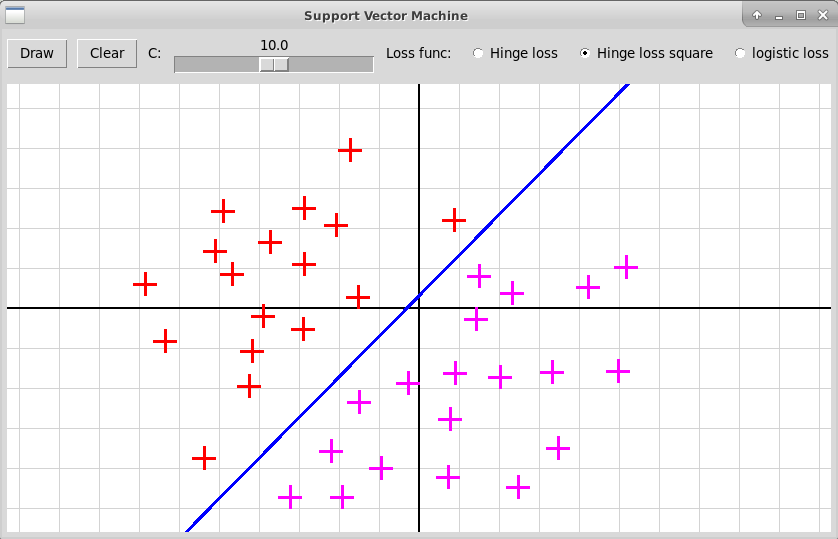
Обозначим это минимальное расстояние через $h$. Точки, находящиеся на расстоянии $h$ до гиперплоскости, называются опорными (support), отсюда и название этого метода (support vector machine).

Применим формулу для расстояния со знаком от точки $p$ до плоскости, заданной уравнением $\langle w, x\rangle - b = 0$: $$ h = (\langle w, p\rangle - b)/|w|, $$ где через $|w|$ обозначена длина вектора нормали $w$. Для опорных точек выполняется условие $$ y_i(\langle w, x_i\rangle - b)/|w| = h, $$ (здесь знак в правой части исчезает за счет домножения на $y_i = \pm 1$). Для всех остальных точек выполняется неравенство: $$ y_i(\langle w, x_i\rangle - b)/|w| \ge h. $$ Отметим, что в данной постановке задачи гиперплоскость определяется только опорными точками (добавление новых точек, расположенных от гиперплоскости дальше опорных, на выбор наилучшей гиперплоскости не влияет).

Домножив неравенство на $1/h$, получим: $$ y_i(\langle w, x_i\rangle - b)/(|w|\cdot h) \ge 1. $$ Обозначим теперь $w' = w\cdot(1/(|w|\cdot h))$, $b' = b/(|w|\cdot h)$. От умножения гиперплоскость не изменится, и точки $x_i$ будут удовлетворять неравенству: $$ y_i(\langle w', x_i\rangle - b') \ge 1. $$ При этом, поскольку $w' = w\cdot(1/(|w|\cdot h))$, то $$ \begin{array}{l} |w'| = |w|/(|w|\cdot h)\quad =\gt \\ h = 1/|w'|. \end{array} $$ Отсюда получаем, что ширина полосы, разделяющей два множества, равна $2h = 2/|w'|$. Чтобы не загромождать обозначения, будем снова обозначать неизвестные параметры гиперплоскости через $w$, $b$ (опустим штрихи). Итак, нам надо максимизировать ширину полосы, разделяющей два класса точек, при том, что все точки одного класса лежат в положительном полупространстве, все точки другого — в отрицательном. Ширина полосы обратно пропорциональна длине вектора нормали $|w|$, значит, нам надо минимизировать $|w|$, или, что то же самое, минимизировать квадрат длины $|w|^2$. Мы пришли к следующей постановке задачи условной минимизации: $$ \begin{array}{l} y_i(\langle w, x_i\rangle - b) \ge 1, \quad i=1,2,\dots,m \\ |w|^2 \to \min. \end{array} $$

Эту задачу можно решать методами математического программирования, применяя теорему Куна-Такера и т.п. Тем не менее мы не будем сейчас рассматривать методы ее решения. Отметим, что в общем случае эта задача неразрешима, когда два множества невозможно разделить никакой гиперплоскостью. Рассмотрение этой задачи нам понадобилось только для того, чтобы обосновать более общую постановку задачи, которая уже имеет решение всегда.

Неразделимый случай

В общем случае система неравенств $$ y_i(\langle w, x_i\rangle - b) \ge 1, \quad i=1,2,\dots,m $$ неразрешима, когда два множества невозможно разделить гиперплоскостью. Ослабим немного эти неравенства: введем переменные $\xi_i$ с ограничениями $\xi_i \ge 0$ и разрешим выражениям для расстояния до гиперплоскости быть чуть меньшими, чем 1, на величины $\xi_i$: $$ y_i(\langle w, x_i\rangle - b) \ge 1 - \xi_i, \quad i=1,2,\dots,m $$ Величины $\xi_i$ выражают как бы нашу плату за нахождение ослабленного решения, когда строгого решения не существует. Нам надо минимизировать эту плату, поэтому мы будем минимизировать не только $|w|^2$, но и сумму ослабляющих переменных (в идеальном случае эта сумма должна быть нулевой): $$ |w|^2 + С\cdot 1/m\sum_{i=1}^m \xi_i \to \min. $$ Здесь константа $C$ — гипер-параметр нашего алгоритма. Чем больше $C$, тем большее значение имеет расположение точек в правильной полуплоскости в соответствии с их классом. При меньших значениях параметра $C$ большее значение придается ширине разделяющего слоя между множествами точек двух классов, параллельного гиперплоскости. Отметим, что слагаемое $|w|^2$ можно рассматривать как параметр регуляризации (он имеет тем большее значение, чем меньше $C$).

Итак, теперь наша задача формулируется следующим образом: $$ \begin{array}{l} |w|^2 + C\cdot 1/m\sum_{i=1}^m \xi_i \to \min \\ y_i(\langle w, x_i\rangle - b) \ge 1 - \xi_i, \quad i=1,2,\dots,m \\ \xi_i \ge 0 \end{array} $$

Это задача условной минимизации. Теперь попробуем исключить переменные $\xi_i$ из нашей системы и получить задачу безусловной оптимизации. Имеем $$ \begin{array}{l} \xi_i \ge 1 - y_i(\langle w, x_i\rangle - b) \\ \xi_i \ge 0 \end{array} $$ Поскольку $\xi_i$ должны быть как можно меньше, но при этом неотрицательные, то для выполнения этих двух условий достаточно выполнения равенства $$ \xi_i = \max(1 - y_i(\langle w, x_i\rangle - b), 0). $$ Теперь, подставив выражение для $\xi_i$ в целевую функцию, получим: $$ |w|^2 + C\cdot 1/m \sum_{i=1}^m \max(1 - y_i(\langle w, x_i\rangle - b), 0) \to \min_{w, b} $$ В результате мы свели нашу задачу поиска условного экстремума к безусловной, которую уже можно решить обычными методами минимизации (градиентный спуск, методы сопряженных градиентов и т.п.).

Функция $$ H(x) = \max(1 - x, 0), \quad x\in \Bbb{R} $$ носит название Hinge Loss. Вот ее график:

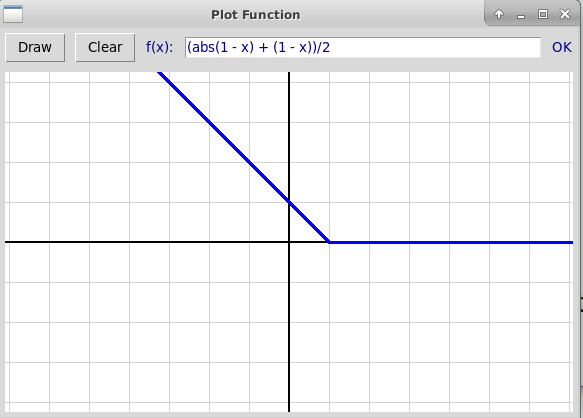
Теперь нашу задачу можно переписать в виде $$ |w|^2 + C\cdot 1/m \sum_{i=1}^m H(y_i(\langle w, x_i\rangle - b)) \to \min_{w, b} $$

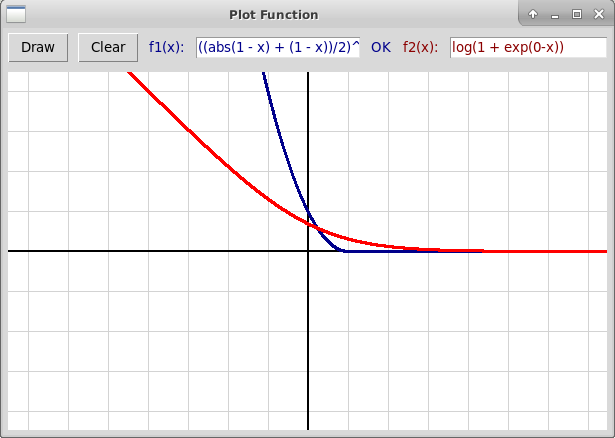
Проблема с этой функцией в том, что она не всюду дифференцируема. Поэтому можно вместо нее использовать либо ее квадрат, либо функцию логистической потери (Logistic Loss): $$ \begin{array}{l} H2(x) = (\max(1 - x, 0))^2 \\ L(x) = \ln(1 + e^{-x}). \end{array} $$ Вот графики этих двух функций:

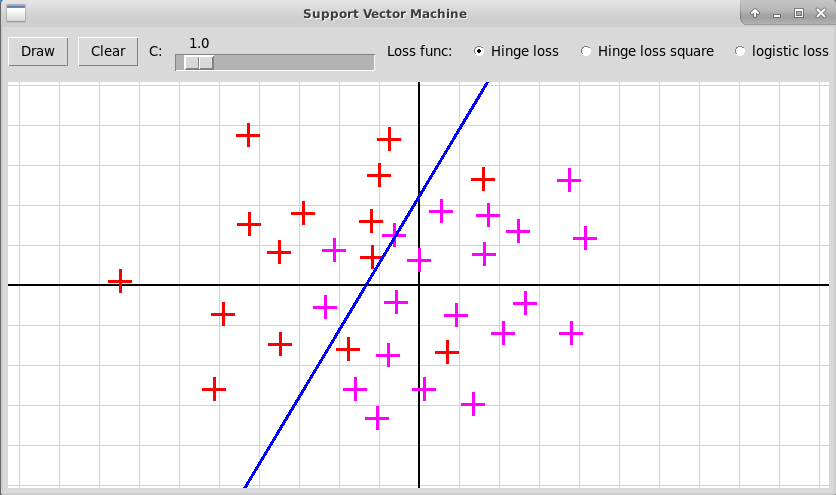
Эксперименты показывают, что с этими двумя функциями качество решения получается лучше, особенно в случае малого числа точек $m$. Три примера приведены на следующих скриншотах (исходники программы на Python'е: "svm.zip").

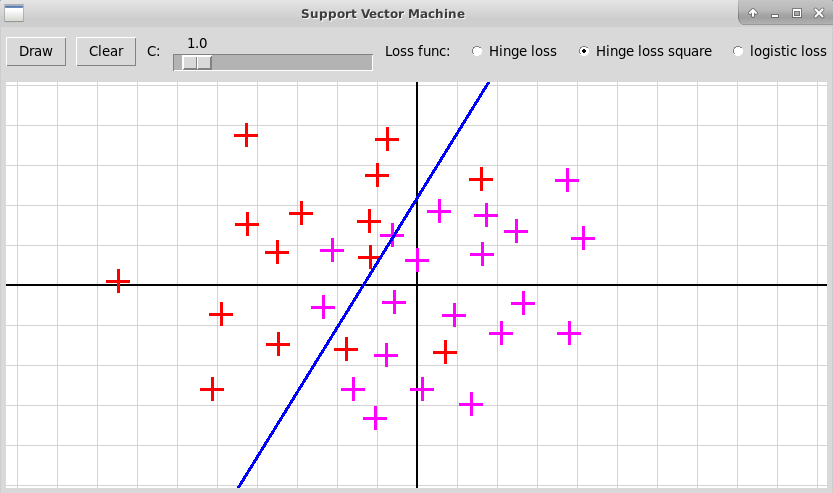
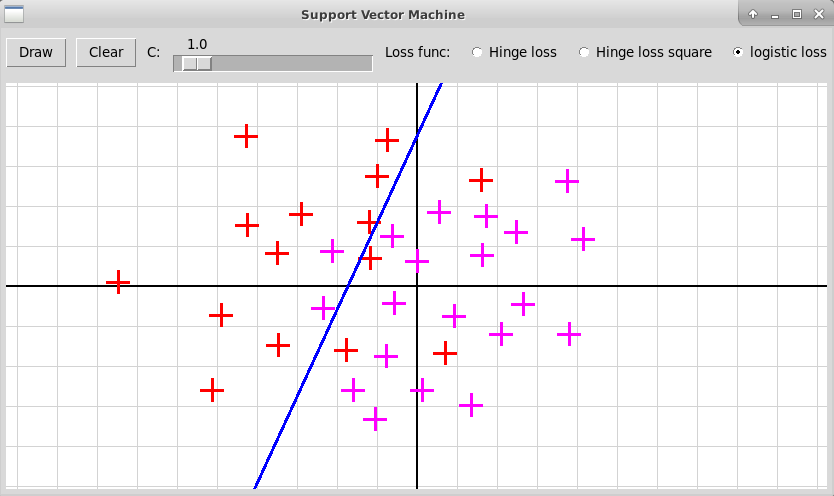
Многоклассовая классификация

Мы рассмотрели задачу бинарной классификации, когда надо разделить множество всех объектов на 2 класса. На практике, однако, часто встречается задача определения класса объекта, когда число возможных классов больше двух. Эту задачу можно свести к бинарной классификации. Мы рассмотрим два способа такого сведения.

Метод "один против остальных" (one-vs.-rest)

Пусть число возможных классов равно $K$. Пусть разметка тренировочных данных, т.е. числа $y_i$, $i=1,\dots,m$, принимает значения из множества $\Bbb{Y}=\{1, 2, \dots, K\}.$ Для каждого класса $k$, где $k = 1, 2, \dots, K$, мы строим классификатор $f_k$, используя следующую разметку данных: $$ \tilde{y}_i = 2(y_i == k) - 1, \quad i = 1,\dots, m. $$ То есть $\tilde{y}_i = 1$, если $y_i = k$, и $\tilde{y}_i = -1$ в противном случае. Мы строим $k$-й классификатор на тренировочном множестве $(x_i, \tilde{y}_i)$, $i=1,\dots, m$.

Пусть построенные с помощью метода опорных векторов классификаторы $f_k$, $k=1,\dots,K$ задаются параметрами $(w_k, b_k)$: $$ f_k(x) = \langle w_k, x \rangle - b_k, \quad w_k\in \Bbb{R}^n,\ b_k \in \Bbb{R}. $$ Здесь гиперплоскость $\langle w_k, x \rangle - b_k = 0$ отделяет точки $k$-го класса от точек всех остальных классов, в положительном полупространстве находятся точки $k$-го класса, в отрицательном — точки всех остальных классов. Отметим, что значение $f_k(x)$ пропорционально расстоянию со знаком от точки $x$ до разделяющей гиперплоскости.

В случае бинарной классификации нас интересовал только знак классификатора $f_k(x)$ (больше или меньше нуля это значение). Но при многоклассовой классификации в методе "один против остальных" нас уже интересует величина числа $f_k(x)$ — чем она больше, тем больше вероятность того, что точка $x$ принадлежить $k$-му классу. Поэтому при определении класса $a(x)$ для точки $x$ мы выбираем тот номер $k$, при котором значение классификатора $f_k(x)$ максимально: $$ a(x) = \text{argmax}_{k\in\{1,2,\dots,K\}} f_k(x). $$ Таким образом, метод "один против остальных" требует построения $K$ классификаторов $f_1(x), f_2(x),\dots, f_K(x)$.

Недостаток метода "один против остальных" состоит в том, что при построении каждого классификатора $f_k(x)$ не предполагается, что его значение будет использоваться для сравнения с другими классификаторами, т.е. у разных классификаторов может быть различная нормировка. Этот недостаток можно преодолеть, используя метод "каждый против каждого".

Метод "каждый против каждого" (one-vs.-one)

В этом методе для каждой пары $(k, l)$ классов мы строим бинарный классификатор $a_{k,l}(x)$, который выдает значения $\pm 1$: единицу, если более вероятно, что точка $x$ принадлежит классу $k$, и минус единицу, если классу $l$. Мы строим классификатор только на том тренировочном подмножестве пар $(x_i, y_i)$, где $y_i\in\{k, l\}$.

Всего в этом методе придется построить $K(K-1)/2$ бинарных классификаторов $a_{k,l}(x)$ для всех упорядоченных пар $(k, l)$, где $1 \le k \lt l\le K$. Можно провести аналогию с баскетбольным турниром $K$ команд по круговой системе (не футбол, поскольку в баскетболе не бывает ничьих). Значением классификатора $a(x)$ будет тот класс $k$, который одерживает максимальное число побед над другими классами (т.е. выигрывает круговой турнир): $$ a(x) = \text{argmax}_{k\in\{1,2,\dots,K\}}( \sum_{1\le l\lt k\le K}(a_{l,k}(x) == -1) + \sum_{1\le k\lt l\le K}(a_{k,l}(x) == 1)) $$ (условие $a_{l,k} == -1$ соответствует победе команды $k$ над командой $l$ на чужом поле, условие $a_{k,l} == 1$ — победе $k$ над $l$ на своем поле; мы считаем, что истинное условие принимает значение 1, ложное 0).