Решение кубического уравнения

Формулу Кардано для решения кубического уравнения не учат ни в школе, ни даже на первом курсе мехмата МГУ. Между тем она не намного сложнее формулы для решения квадратного уравнения, вывести ее ничего не стоит, причем не нужно ничего запоминать, чтобы вывести ее при необходимости еще один раз. При этом кубические уравнения на практике возникают очень часто — например, для вычисления собственных чисел и векторов матрицы $3\times 3$, которая реализует преобразование трехмерного пространства, надо решить ee характеристическое уравнение третьей степени.

Кубическое уравнение в общем случае записывается так: $$ ax^3 + bx^2 + cx + d = 0. $$ Упростим уравнение. Во-первых, делая замену $x = x' + s$, можно избавиться от коэффициента $b$ при второй степени $x$: $$ a(x'+s)^3 + b(x'+s)^2 + c(x'+s) + d = 0 \\ ax'^3 + (3as + b)x'^2 + \ldots = 0. $$ Достаточно положить $s = -b/(3a)$. Кроме того, разделив уравнение на $a$, можно считать, что коэффициент при $x^3$ равен $1$.

Итак, будем считать, что уравнение изначально имеет вид $$ x^3 + ax + b = 0. $$ Главный трюк при решении этого уравнения состоит в том, что мы делаем замену $$ x = u + v, $$ что позволяет нам перейти от одного уравнения с одним неизвестным к системе из двух уравнений с двумя неизвестными. Такой переход, казалось бы, от простого к сложному позволит нам легко решить уравнение.

Сделав эту замену, получим: $$ (u+v)^3 + a(u+v) + b = 0, \\ u^3 + 3 u^2 v + 3 u v^2 + v^3 + a(u + v) + b = 0, \\ u^3 + 3 uv(u + v) + v^3 + a(u + v) + b = 0, \\ u^3 + v^3 + b + (u + v)(3uv + a) = 0. $$ Отметим, что нам достаточно найти хотя бы один корень уравнения. Найдя корень $x = x_0$, мы разделим кубический многочлен на $(x - x_0)$ с остатком. Так как $x_0$ — корень, то остаток равен нулю, и мы сведем нахождение двух других корней к решению уже квадратного уравнения.

Теперь разобьем полученное уравнение на две части: $$ [u^3 + v^3 + b] + [(u + v)(3uv + a)] = 0. $$ Сумма равна нулю, если оба слагаемых равны нулю, значит, для нахождения одного решения достаточно решить систему уравнений: $$ \left\{ \begin{array}{l} u^3 + v^3 + b = 0 \\ (u + v)(3uv + a) = 0 \end{array} \right. $$ Если в исходном уравнении $b\ne 0$, то $x=0$ не является решением. Поскольку $x=u+v$, то второе уравнение системы можно сократить на $(u+v)$. Получим: $$ \left\{ \begin{array}{l} u^3 + v^3 + b = 0 \\ 3uv + a = 0 \end{array} \right. $$ Выразим $v$ через $u$ из второго уравнения и подставим в первое уравнение: $$ \left\{ \begin{array}{l} u^3 - a^3/(27u^3) + b = 0 \\ v = -a/(3u) \end{array} \right. $$

Сделав замену $u^3 = y$ в первом уравнении, мы получим квадратное уравнение относительно $y$: $$ y - a^3/(27y) + b = 0, \\ 27y^2 + 27by - a^3 = 0. $$ Решаем последнее квадратное уравнение: $$ D = 27^2 b^2 + 4\cdot 27 a^3 = 9(81b^2 + 12a^3) \\ y = (-27b \pm \sqrt{D})/54 = (-27 \pm 3\sqrt{81b^2 + 12a^3})/54 = \\ = (-9b \pm \sqrt{81b^2 + 12a^3})/18. $$ Поскольку нам достаточно найти хотя бы одно решение, то выберем знак $+$ в формуле: $$ y = (-9b + \sqrt{81b^2 + 12a^3})/18. $$ Здесь квадратный корень — это либо вещественное, либо чисто мнимое комплексное число, в зависимости от знака дискриминанта, если мы рассматриваем исходное уравнение с вещественными коэффициентами. Если изначально мы рассматриваем уравнение с комплексными коэффициентами, то выбираем любой из двух комплексных корней из дискриминанта.

Пример

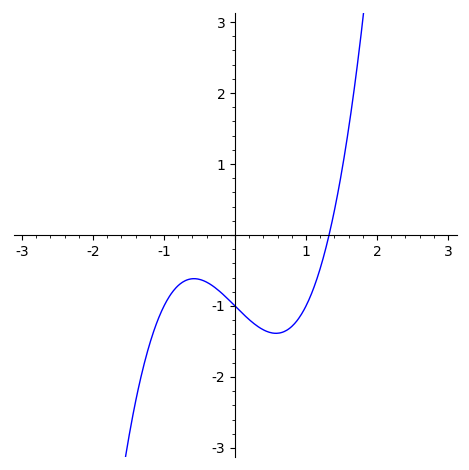
Найдем вещественный корень уравнения $$ x^3 - x - 1 = 0 $$ (это очень важное уравнение, возникающее, например, совершенно неожиданно в программировании при реализации динамического массива, здесь $x$ — знаменатель геометрической прогрессии, с которой растет объем памяти динамического массива, вернее, верхнее ограничение для этого знаменателя из условия того, что освобожденная на предыдущих шагах память может снова быть использована).

По выписанным выше формулам вычисляем: $$ y = (9 + \sqrt{81 - 12})/18 = \sqrt{69}/18 + 1/2, \\ u = y^{1/3} = (\sqrt{69}/18 + 1/2)^{1/3},\quad v = 1/(3u),\\ x = u + v = (\sqrt{69}/18 + 1/2)^{1/3} + 1 / (3(\sqrt{69}/18 + 1/2)^{1/3}). $$ Вычислим приближенное значение $x$, последовательно применяя эти формулы: $$ y = \sqrt{69}/18 + 1/2 \approx 0.961479103495449, \\ u = y^{1/3} \approx 0.986991206271354, \\ v = 1/(3u) \approx 0.337726750973392, \\ x = u + v \approx 1.32471795724475. $$ Ответ правильный, что подтверждает график функции $f(x) = x^3 - x - 1$: