
1.10 Статистическая независимость
Теперь мы распространим понятие независимости на случай произвольного конечного
набора событий
![]() . Мы обсудим два способа распространения Определения 1.6,
а именно, понятия взаимной независимости и попарной независимости.
Начнем с первого из них.
. Мы обсудим два способа распространения Определения 1.6,
а именно, понятия взаимной независимости и попарной независимости.
Начнем с первого из них.
В литературе употребляются следующие термины-синонимы:
События
![]() --
-- 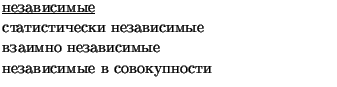
Рассмотрим теперь второе, более слабое определение независимости.
| Независимость |
|
попарная независимость |
|
|
Первая импликация вытекает из Определений 1.7 и 1.8. Следующий пример показывает, что события могут быть попарно независимыми, но зависимыми в совокупности.
![]() на первой кости выпало нечетное число очков
на первой кости выпало нечетное число очков ![]() ,
,
![]() на второй кости выпало нечетное число очков
на второй кости выпало нечетное число очков ![]() ,
,
![]() сумма очков -- нечетна
сумма очков -- нечетна ![]() .
.
События ![]() -- попарно независимые. Действительно,
-- попарно независимые. Действительно,
Из Упражнений 1.2 и 1.3 вытекает, что