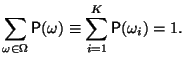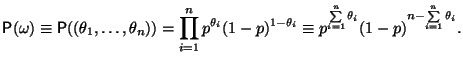1.1 Конечное вероятностное пространство
В истоках любых математических построений лежат понятия множества и отображения (функции). Мы начнем с изложения формальной схемы, постепенно устанавливая на примерах необходимые параллели со случайными явлениями реального мира.
Рассмотрим
произвольное конечное множество
![]() , которое
впредь будем называть множеством элементарных исходов,
а его элементы
, которое
впредь будем называть множеством элементарных исходов,
а его элементы
![]() -- элементарными исходами.
-- элементарными исходами.
Пусть задана функция
![]() . То есть, каждому
элементарному исходу
. То есть, каждому
элементарному исходу ![]() поставлено в соответствие число
поставлено в соответствие число
![]() из отрезка
из отрезка ![]() .
.
Будем предполагать, что
Функцию
Пару
![]() , составленную из множества
, составленную из множества ![]() и функции
и функции
![]() ,
удовлетворяющих перечисленным выше требованиям, мы назовем конечным вероятностным
пространством.
,
удовлетворяющих перечисленным выше требованиям, мы назовем конечным вероятностным
пространством.
В дальнейшем, через
![]() мы обозначаем число
элементов в множестве
мы обозначаем число
элементов в множестве ![]() .
.
Очевидно, что
Число элементов в этом множестве:
Заметим, что при
Схема испытаний Бернулли является важной в теоретическом и прикладном плане
вероятностной моделью. Эта модель интерпретируется следующим образом: последовательно
проводится серия из ![]() однородных отдельных испытаний, каждое из которых
может завершиться лишь одним из двух вариантов
однородных отдельных испытаний, каждое из которых
может завершиться лишь одним из двух вариантов ![]() и
и ![]() . Таким
образом, элементарный исход
. Таким
образом, элементарный исход
![]() представляет собой ``протокол'' проведенной серии из
представляет собой ``протокол'' проведенной серии из ![]() испытаний.
Согласно установившейся традиции, если
испытаний.
Согласно установившейся традиции, если
![]() , то говорят, что
, то говорят, что
![]() -е испытание завершилось ``успехом''; если
-е испытание завершилось ``успехом''; если
![]() ,
то говорят, что
,
то говорят, что ![]() -е испытание завершилось ``неуспехом''.
-е испытание завершилось ``неуспехом''.
Схема Бернулли широко применяется в различных задачах, и мы неоднократно будем к ней возвращаться в дальнейшем.
|
След.: 1.2 Понятие события ...
Пред.: 1 События и их ... Вверх: 1 События и их ... |
Оглавление
Предметный указатель |