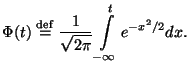3.6 Понятие о квантилях ... 3 Общие случайные величины ... 4 Совместное распределение общих ...

3.7 Нормальное распределение

Функция распределения стандартного нормального закона  , ввиду ее важности имеет специальное обозначение

(19)

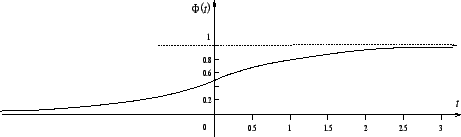
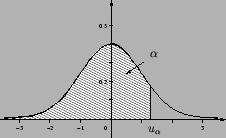
Квантили этого распределения мы будем обозначать : .





Функция не является элементарной, то есть, интеграл в (19) не может быть сведен к табличным и быть композицией элементарных функций. Для функции составлены подробные таблицы, ее значения вычисляются многими прикладными компьютерными программами. В настоящей брошюре таблица значений функции  приводится на стр. [*]-[*]. С их помощью, например, можно найти, что

(20)

По Предложению 3.3 имеем тождества

     
    (21)

Если имеет распределение , то -- стандартная нормальная случайная величина (см. по этому поводу Упражнения 3.6 и 3.7). Функция распределения легко записывается через функцию :

Из свойства (18) вытекает, что

Полагая и и учитывая (21), получим

В частности, приравнивая  , находим и, вспоминая (20), приходим к так называемому правилу ``трех сигм'':

(22)

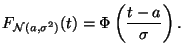
Вероятность, которая стоит в правой части, пренебрежимо мала для многих практических применений. Поэтому правило ``трех сигм'' читают так: нормальная случайная величина уклоняется от своего среднего не более, чем на три корня из дисперсии. Как мы видим из (22), это правило ошибочно лишь в случаев.

Упражнение 3.10  

При помощи таблиц найти вероятности и .

В заключение, приведем значения наиболее употребительных квантилей стандартного нормального закона2.



.50 0 .91 1.341 .995 2.576
.55 .126 .92 1.405 .999 3.090
.60 .253 .93 1.476 .9995 3.291
.65 .385 .94 1.555 .9999 3.719
.70 .524 .95 1.645 .99995 3.891
.75 .674 .96 1.751 .99999 4.265
.80 .842 .97 1.881 .999995 4.417
.85 1.036 .98 2.054 .999999 4.753
.90 1.282 .99 2.326 .9999999 5.199



След.: 4 Совместное распределение общих ...
Пред.: 3.6 Понятие о квантилях ...
Вверх: 3 Общие случайные величины ... 		  Оглавление
  Предметный указатель
 

А.Д. Манита, 2001-2011