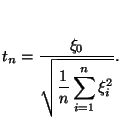8.2 Вероятностные распределения, связанные с нормальным
Подпункты этого параграфа:
Здесь мы кратко обсудим распределение хи-квадрат и
распределение Стьюдента, играющие исключительную роль в статистике. Наше изложение
близко содержанию
![]() 2.6 книги [13].
2.6 книги [13].
Хи-квадрат распределение
Пусть
![]() -- независимые стандартные нормальные случайные
величины
(
-- независимые стандартные нормальные случайные
величины
(![]() ).
). ![]() -распределением
с
-распределением
с ![]() степенями свободы называется распределение следующей случайной величины:
степенями свободы называется распределение следующей случайной величины:
Это распределение сосредоточенно на положительной полуоси и имеет плотность
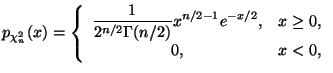
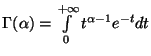 -- гамма-функция.
-- гамма-функция.
Начертить графики плотности
![]() при
при ![]() и
и ![]() .
.
Найти
![]() и
и
![]() .
.
Квантили распределения
![]() будем обозначать
будем обозначать
![]() ,
,
![]() . По определению они являются решениями уравнения
. По определению они являются решениями уравнения
где
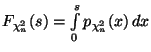 -- функция хи-квадрат распределения с
-- функция хи-квадрат распределения с
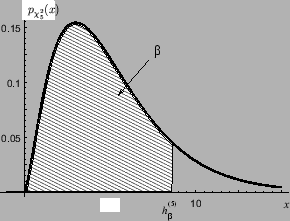
Для значений функции распределения
![]() имеются таблицы,
из которых находят квантили. Кроме этого, хи-квадрат распределение интегрировано
в большое число прикладных компьютерных программ [13]. На странице
имеются таблицы,
из которых находят квантили. Кроме этого, хи-квадрат распределение интегрировано
в большое число прикладных компьютерных программ [13]. На странице ![[*]](crossref.png) настоящей брошюры также приведена небольшая таблица квантилей хи-квадрат распределения.
настоящей брошюры также приведена небольшая таблица квантилей хи-квадрат распределения.
Распределение Стьюдента
Это распределение получило свое название от псевдонима Student, которым английский ученый Госсет подписывал свои работы по статистике.
Пусть
![]() -- независимые стандартные нормальные
случайные величины. Распределением Стьюдента
с
-- независимые стандартные нормальные
случайные величины. Распределением Стьюдента
с ![]() степенями свободы называется распределение следующей случайной величины:
степенями свободы называется распределение следующей случайной величины:
Если вспомнить введенную формулой (44) случайную величину
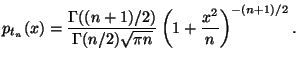
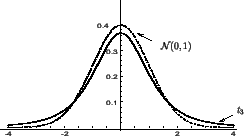
На чертеже представлены плотность распределения Стьюдента ![]() и плотность
стандартного нормального закона.
и плотность
стандартного нормального закона.
В дальнейшем нам понадобятся квантили распределения ![]() , которые мы
будем обозначать
, которые мы
будем обозначать
![]() ,
,
![]() ,
,
![[*]](crossref.png) .
.
|
След.: 8.3 Теорема Фишера для ...
Пред.: 8.1 Понятие доверительного интервала ... Вверх: 8 Доверительные интервалы ... |
Оглавление
Предметный указатель |