Самостоятельная работа состоит в решении задач по темам, которые обсуждаются в лекциях. По каждой теме нужно решить одну задачу из предлагаемого списка. Номер задачи равен номеру студента в журнале по модулю n, где n — число задач по данной теме.

Классы в С++

Трехмерная графика и аналитическая геометрия

Классы для поддержки двумерной и трехмерной графики

Для вычислений на плоскости R² используются классы R2Vector (вектор на плоскости с вещественными координатами) и R2Point (точка на плоскости). В пакете "R2Graph.zip" реализованы все основные операции на плоскости

Простой пример программы, использующей классы R2Point и R2Vector и потоковый ввод-вывод в стиле C++: ввести вершины треугольника и вычислить центр и радиус вписанной окружности. При вычислении запрещено использовать координаты векторов и точек, следует пользоваться исключительно методами классов R2Point и R2Vector. Файл "inCircle.cpp". Программа использует модуль R2Graph, в котором определяются классы для поддержки геометрии на плоскости: файлы "R2Graph.h" и "R2Graph.cpp". Архив всех файлов: "InCircle.zip"

Задачи на использование классов в R²-графике

1. Вычислить центр и радиус окружности, описанной вокруг треугольника.
2. Вычислить точку пересечения высот треугольника.
3. Вычислить точку Жергона:
   
   (это точка пересечения чевиан, проведенных из вершин треугольника к точкам касания вписанной окружности).

Трехмерная геометрия: координаты на поверхности Земли и на карте

Мы используем классы R3Vector и R3Point, реализующие точки и векторы трехмерного пространства, для работы с картами земной поверхности. Координаты на поверхности Земли задаются широтой и долготой в градусах. Долгота точки — это угол между плоскостью гринвичского меридиана и плоскостью меридиана, проходящего через данную точку. Широта — это угол между радиус вектором, проведенным из центра Земли в данную точку, и плоскостью экватора. Эти углы измеряются в градусах. Долгота положительна для восточного полушария (и растет по мере продвижения на восток) и отрицательна в западном полушарии. Широта положительна в северном полушарии и отрицательна в южном.

Рассмотрим классическую задачу определения расстояния между двумя точками на поверхности Земли (приблизительно считаем поверхность Земли сферой). Самый простой способ ее решения — это найти угол между радиус-векторами, проведенными из центра Земли к этим точкам, и умножить его на радиус Земли. В классе R3Vector имеется метод angle, возвращающий угол между векторами, мы им воспользуемся. Все, что нам нужно — это реализовать функцию, определяющую радиус-вектор единичной длины, проведенный из центра Земли в направлении заданной точки.

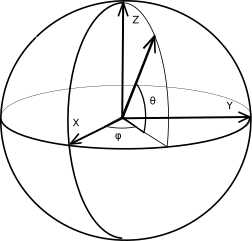
Для представления векторов и точек на поверхности Земли мы используем декартову систему координат, у которой начало координат расположено в центре Земли. Ось x направлена из центра в точку перечесения экватора и гринвичского меридиана, ось z направлена на северный полюс, ось y перпендикулярна осям z и x и направлена на восток.

Радиус-вектор единичной длины, направленный из центра земли в точку с широтой и долготой (lat, lon), получается из базисного вектора e_x двумя поворотами: первый поворот на угол lon выполняеся вокруг оси z, второй поворот на угол lat выполняется в меридиональной плоскости. После первого поворота мы получаем вектор

R3Vector radiusVector(double lat, double lon) {
    double phi = lon*PI/180.;   // Convert to radians
    double theta = lat*PI/180.;
    
    // Rotate ex around ez by angle phi: v0 = (cos(phi), sin(phi), 0.)
    // Rotate v0 in meridional plane by angle theta:
    // v1 = (cos(phi)*cos(theta), sin(phi)*cos(theta), sin(theta))
    double cosTheta = cos(theta);
    return R3Vector(cos(phi)*cosTheta, sin(phi)*cosTheta, sin(theta));
}

Полный текст программы: "earthdist.cpp". Проект использует также файлы "R3Graph.h" и "R3Graph.cpp", команда для компиляции проекта в Linux'е:

    g++ -o earthdist earthdist.cpp R3Graph.cpp

Задачи на использование классов в R³-графике

Карта представляет собой касательную плоскость к земной сфере. Положение карты задается координатами ее центра: (широта центра, долгота центра). Для представления точек поверхности сферы на карте используется центральная проекция с центром в центре земного шара. На карте используется декартова система координат, в которой ось Y направлена на север (касательная к меридиану, проходящему через центр карты), ось X перпендикулярна оси Y и направлена на восток. Нужно решить одну из следующих двух задач (студенты с нечетными номерами решают 1-ю задачу, с четными — вторую).

1. Заданы координаты центра карты (mlat, mlon) и координаты точки на земной поверхности (lat, lon) в градусах. Получить координаты проекции этой точки на карте (x, y) в метрах.
2. Заданы координаты центра карты (mlat, mlon) и координаты точки (x, y) на карте в метрах. Получить координаты точки на поверхности Земли (lat, lon) в градусах, которая проецируется в данную точку на карте.

Реализация классов на C++

Примеры классов, реализующих математические объекты

1. Комплексное число: class Complex. Файлы "Complex.h", "Complex.cpp", тестовая программа "complexTst.cpp".
2. Элемент кольца вычетов по модулю m: class Zm. Файлы "Zm.h", "Zm.cpp", тестовая программа "tstZm.cpp".
   Видео лекции 18.09.2020 (вторая половина).
3. Матрица над полем вещественых чисел: class Matrix. Файлы "Matrix.h", "Matrix.cpp", тестовая программа "matrixTest.cpp".

Задачи по теме "Реализация классов"

В каждой задаче надо реализовать класс, представляющий некоторый математический объект, и написать программу, использующую этот класс. Например, реализовать класс Complex и с помощью этого класса написать программу, решающую кубическое уравнение (используя формулу Кардано или другую подобную). В простейшем случае надо хотя бы написать тестирующую программу, создающие объекты и вызывающую различные методы класса. Обязательно класс должен быть описан в отдельном h-файле. Также должен быть cpp-файл, который реализует сложные (не inline) методы класса. Например, для класса матриц метод Гаусса приведения матрицы к ступенчатому виду должен быть реализован в cpp-файле (ни в коем случае не в h-файле!). Таким образом, проект должен состоять минимум из трех файлов. Например, тестовый проект для класса Complex состоит из трех файлов:
Complex.h, Complex.cpp, complexTst.cpp.

Также надо написать Makefile, Например, для класса Complex можно в Unix'е или в MAC OS-X использовать файл

CC = g++ $(CFALGS)
# For debugging
CFLAGS = -O0 -g

complexTst: Complex.h Complex.cpp complexTst.cpp
        $(CC) -o complexTst complexTst.cpp Complex.cpp

clean:
        rm -f complexTst

Список задач по теме "Реализация классов"

1. Реализовать класс Complex, представляющий комплексные числа. При этом требуется использовать внутреннее представление комплексных чисел в экспоненциальной форме:
   
   z = r·e^iφ
   Воспользовавшись этим классом, написать программу, решающую кубическое уравнение с помощью формулы Кардано (или чего-то похожего). Описание см. в статье Решение кубического уравнения.
2. Реализовать класс Polynomial, представляющий многочлен произвольной степени с коэффициентами в поле вещественных чисел. Должны быть реализованы операции сложения, умножения, деления с остатком, вычисление наибольшего общего делителя многочленов, производной многочлена, а также вычисление многочлена с теми же корнями, свободного от кратных корней, т.е. частного от деления многочлена f на gcd(f, f').
3. Та же задача, но для многочленов над полем Z_p.
4. Реализовать класс "Элементы поля GF_p²", где p — простое число. См. статью Конструкция конечного поля из p² элементов.
5. Реализовать класс "Матрицы порядка m×n над полем вещественных чисел". Должны быть реализованы операции +, -, * над матрицами, приведение матрицы к ступенчатому виду, вычисление ранга, а также для квадратной матрицы вычисление определителя и обратной матрицы и решение линейной системы с невырожденной матрицей.
6. Та же задача, но для матриц над полем Z_p.

Проект "Стековый калькулятор"

Стековый калькулятор — это калькулятор, память которого представляет собой стек. При выполнении любой операции ее аргументы сначала извлекаются из стека, затем выполняется операция и ее результат добавляется обратно в стек. Таким образом, агрументы операции должны быть положены в стек перед ее выполнением. Программа вычисления значения формулы на стековом калькуляторе соответствует обратной польской записи формулы, в которой знак операции указывается после ее аргументов. Пример:

Обратную запись формул предложил польский математик Ян Лукасиевич, в его честь она называется польской. Помимо обратной записи, он также предложил и прямую, в которой знак операции указывается перед аргументами. Например, та же формула

Вернемся к обратной польской записи формулы:

+---+ | 1 | | 2 | | 3 | / |2/3| + |5/3| | 4 | |56 | + |60 | * |100|
      +---+ | 1 | | 2 |   | 1 |   +---+ |5/3| | 4 |   |5/3|   +---+
            +---+ | 1 |   +---+         +---+ |5/3|   +---+
                  +---+                       +---+

Исходный код проекта "Стековый калькулятор": "StackCalc.zip".

Домашнее задание по проекту "Стековый калькулятор"

Студенты с нечетными номерами по журналу делают первую задачу, с четными — вторую.

1. Добавьте операцию возведения в степень, которая обозначается значком ^ (крышка) или ** (двойная звездочка), а также возможность вычисления следующих математических функций:
   sin(x), cos(x), exp(x),
   log(x) (натуральный), log2(x), log10(x),
   tan(x), atan(x), atan2(y, x),
   cosh(x), sinh(x), tanh(x),
   abs(x), min(x, y), max(x, y), pow(x, y),
   powmod(a, n, m), gcd(m, n), invmod(k, m).
   
   Последние три функции работают с целыми числами типа long long, при снятии аргументов со стека и при добавлении результата в стек должно выполняться преобразование типов double → long long или long long → double.
2. Воспользовавшись классами R2Vector и R2Point из проекта "R2Graph.zip", добавьте в стековый калькулятор следующие команды для решения геометрических задач на плоскости:

   distance	Расстояние между двумя точками
   distanceToLine	Расстояние от точки до прямой
   intersectLines	Найти точку пересечения двух прямых
   inCircle	Вычислить окружность, вписанную в треугольник
   circumCircle	Вычислить окружность, описанную вокруг треугольника

   При выполнении команды со стека должны сниматься ее аргументы, после необходимых вычислений в стек должны добавляться ее результаты. Например, при вычислении расстояния от точки до прямой на стеке должны лежать 6 чисел: координаты точки, от которой мы ищем расстояние, координаты точки и направляющего вектора, задающих прямую. Они извлекаются из стека (с учетом порядка, в котором они добавлялись: на вершине стека лежит последний аргумент!), выполняются необходимые вычислния, на стек кладется результат — расстояние от точки до прямой (одно число).

   Помимо добавления результата операции в стек, нужно также напечатать результат выполнения операции (число, точку или окружность). Окружность представляется ее центром и радиусом. В этой задаче обязательно надо использовать модуль "R2Graph.zip" и определенные в нем классы и функции, решение с непосредственными вычислениями через координаты не принимается!

Схема построения цикла с помощью инварианта

Лекция 9 октября 2020. Схема построения цикла с помощью инварианта и ее применение на примере ряда алгоритмов: алгоритм Евклида вычисления наибольшего общего делителя двух целых чисел, алгоритм быстрого возведения в степень, расширенный алгоритм Евклида, вычисление логарифма с заданной точностью. Видео лекции.
Исходные тексты перечисленных алгоритмов на C++: файл "gcd.cpp".

Сортировка

Лекция Алгоритмы сортировки (презентация)

Видео лекции 23 октября 2020: оптимальные алгоритмы сортировки. Сортировка кучей Heap Sort, сортировка слиянием Merge Sort (рекурсивная схема реализации).

Задачи по теме "Сортировка"

В каждой задаче надо реализовать один из оптимальных алгоритмов сортировки, работающих за время O(n log n). При этом уже заданы прототипы функций сортировки, которые надо реализовать. В качестве образца для первых трех задач дается программа "tstSort.cpp", в которой реализованы только функции наивной сортировки (bubbleSort и directSort) и некоторые вспомогательные функции (bubbleDown, merge, printArray), а сами функции сортировки оставлены для самостоятельной реализации — выписаны только прототипы функций сортировки и реализована тестирующая программа. Тестирующая программа генерирует случайной массив вещественных чисел заданной длины, печатает исходный массив, затем вызывает одну из функций сортировки и печатает упорядоченный массив, который получается в результате ее выполнения.

Все функции сортировки могут упорядочивать не весь массив целиком, а некоторый его сегмент. Сегмент задается двумя итераторами first и last: итератор first указывает на начало сортируемого сегмента массива, итератор last — на элемент, которые следует за последним элементом сортируемого сегмента. Функции сортировки должны иметь следующие прототипы:

void heapSort(
    std::vector<double>::iterator first, // Beginning of array segment
    std::vector<double>::iterator last   // After-end of array segment
);

void mergeSortRecursive(
    std::vector<double>::iterator first, // Beginning of array segment
    std::vector<double>::iterator last,  // After-end of array segment
    std::vector<double>* tmpMemory = 0   // Temporary memory to use
);

void mergeSortBottomTop(
    std::vector<double>::iterator first, // Beginning of array segment
    std::vector<double>::iterator last,  // After-end of array segment
    std::vector<double>* tmpMemory = 0   // Temporary memory to use
);

void radixSort(
    std::vector<std::string>::iterator first,
    std::vector<std::string>::iterator last,
    int compareLength = 64
);

В четвертой задаче надо применить алгоритм RadixSort для сортировки строк ограниченной длины. На вход алгоритму подается массив строк типа std::string и ограничение compareLength на длину строки (точнее, строки могут быть длиннее, чем compareLength, но сравниваются они только по первым compareLength символам). Строки сравниваются лексикографически по их началам длины compareLength (значение по умолчанию 64). Если строка короче, чем compareLength, то она при сравнении мысленно дополняется пробелами справа. Отметим, что в стандартной библиотеке STL языка C++ класс std::string реализует корректно лишь строки ASCII-символов, для символов Unicode этот класс может работать некорректно (в частности, если строка типа std::string содержит последовательность байтов, которые кодируют строку в кодировке UTF-8, то результат побайтового сравнения строк будет некорректным для символов, не входящих в набор ASCII).

Список задач по теме "Сортировка"

Студент должен решить ту задачу, номер которой совпадает по модулю 4 с его номером по журналу.

1. Реализовать алгоритм сортировки кучей Heap Sort. Прототип функции:

   void heapSort(
       std::vector<double>::iterator first, // Beginning of array segment
       std::vector<double>::iterator last   // After-end of array segment
   );
   

2. Реализовать алгоритм сортировки слиянием Merge Sort, используя рекурсивную схему его реализации. Прототип функции:

   void mergeSortRecursive(
       std::vector<double>::iterator first, // Beginning of array segment
       std::vector<double>::iterator last,  // After-end of array segment
       std::vector<double>* tmpMemory = 0   // Temporary memory to use
   );
   

3. Реализовать алгоритм сортировки слиянием Merge Sort, используя восходящую схему его реализации. Прототип функции:

   void mergeSortBottomTop(
       std::vector<double>::iterator first, // Beginning of array segment
       std::vector<double>::iterator last,  // After-end of array segment
       std::vector<double>* tmpMemory = 0   // Temporary memory to use
   );
   

4. Реализовать алгоритм сортировки Radix Sort для массива ASCII-строк типа std::string. Прототип функции:

   void radixSort(
       std::vector<std::string>::iterator first,
       std::vector<std::string>::iterator last,
       int compareLength = 64
   );
   

   Образец тестирующей программы содержится в файле "radixSort.cpp", она содержит код, генерирующий случайные строки, функцию наивной сортировки прямым выбором directSort, а также прототип функции radixSort. Сама функция radixSort в этом файле не реализована, ее нужно реализовать самостоятельно.

Обработка текстов

Функции для работы с символами в кодировке UTF-8: "utf8.h", "utf8.cpp".

Программа нахождения множества русских слов в тексте: "russianWords.cpp". Для каждого слова определяется количество его вхождений в текст. В результате печатается список слов, упорядоченных по количеству вхождений слов в текст, а для слов с одинаковым числом вхождений — лексикографически.

Программа "russianWords.cpp". использует классы std::map, std::basic_string, std::vector и алгоритм std::sort из стандартной библиотеки, а также функции для работы с Unicode-символами в кодировке UTF8 — файлы "utf8.h", "utf8.cpp". Архив всех файлов проекта: "russianWords.zip".

Список задач на тему "Обработка текстов"

1. Найти и упорядочить множество пар соседних слов в тексте на русском языке. Два соседних слова образуют пару, если между ними нет знаков препинания и других символов, кроме пробелов, переводов строк и дефисов. Пары слов упорядочиваются по количеству вхождений в текст, а для пар с равным числом вхождений — лексикографически. Напечатать 500 самых часто встречающихся пар.
2. Найти и упорядочить множество биграмм в тексте и напечатать их список, упорядоченный по частотам вхождения в текст. (Нужно напечатать только первые 100 биграмм.)
3. Реализовать шифр Виженера для текста на русском языке. Шифруются только русские слова, все остальные символы, включая пробелы и переводы строк, исключаются из зашифрованного текста. Ключевая фраза также на русском языке, все прописные буквы заменяются строчными. Должны быть реализованы 2 программы: шифрование и дешифровка.

Программирование в среде Qt

Qt (Quazar Technology) — самая современная и самая лучшая среда для разработки C++ приложений. К достоинствам Qt относятся:

1) независимость текста программы от компьютера и операционной системы — исходные коды приложения одинаковы в Linux, MS Windows, Mac OS-X, и любых других современных операционных системах. В Qt можно создавать программы как для обычных компьютеров (Desktop), так и для операционных систем мобильных телефонов;

2) удобство программирования оконных и параллельных приложений благодаря удачному механизму сигналов и слотов;

3) поддержка огромного набора файловых форматов, сетевых протоколов и устройств;

4) программы на Qt, как правило, намного эффективнее, чем программы, подготовленные в других средах или на других языках, благодаря тому, что исполняющая система Qt автоматически учитывает особенности каждого конкретного компьютера и, к примеру, выбирает самый эффективный метод реализации графики (как правило, через трехмерный интерфейс, если в компьютере есть современная графическая карта);

5) Qt имеет очень удобную среду разработки qtcreator, которая позволяет редактировать оконные формы и добавлять обработчики сигналов, посылаемых управляющими элементами окон; qtcreator синхронно вносит изменения в h- и cpp-файлы.

Qt использует небольшое расширение базового языка C++ — добавлены ключевые слова signal, emit, slot, connect. Сигналы посылаются, например, управляющими элементами окон (для посылки сигнала используется ключевое слово emit). Слоты — это методы, предназначенныедля приема и обработки сигналов. С помощью вызова connect можно связать сигнал, посылаемый некоторым объектом, с обрабатывающим его слотом. При этом обработка выполняется не сразу путем вызова функции, а с помощью постановки сообщения о сигнале в очередь для последующей обработки объектом, принимающим этот сигнал. Такой способ гораздо более гибкий и безопасный, что важно при асинхронной обработке событий в многопоточных программах с параллельным исполнением нескольких нитей. Специальная утилита moc (Meta-Object Compiler) переводит программу с расширения языка С++ на чистый С++. Qt, в отличие от С++ варианта языка CLR-C++ (Сommon Language Runtime), являющегося частью платформы .Net фирмы Microsoft, не использует управляемую динамическую память и сборщик мусора. Благодаря этому Qt-программы быстрее, более надежны и тратят меньше памяти при выполнении, что позволяет использовать их в системах реального времени.

В Qt в основном разрабатываются оконные графические программы. Примеры программ, разработанных с помощью Qt:

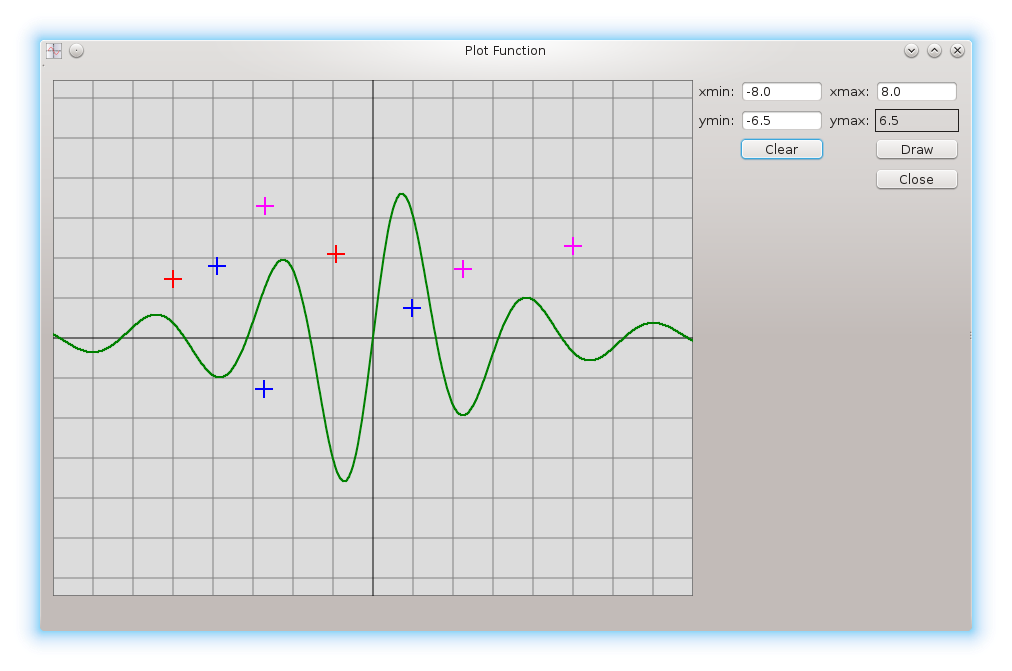
• Qt-проект "График функции": PlotFunc.zip.
  В программе реализовано рисование графика произвольной функции от переменной x. Функция задается формулой, которая записывается в текстовом поле окна. Проект включает в себя парсер формул от одной или двух переменных x, y, получающий по текстовой записи формулы ее обратную польскую запись, которая затем используется для вычисления значений функции.
  
• Qt-проект "Интерполяционный полином Ньютона": NewtonPol.zip.
  По точкам, отмеченным кликами мыши, строится график интерполяционного многочлена. Удобно использовать интерполяционный многочлен в форме Ньютона:

    p_n(x) = a₀ + a₁(x-x₀) + a₂(x-x₀)(x-x₁) + a₃(x-x₀)(x-x₁)(x-x₂) + . . .
         + a_n(x-x₀)(x-x₁)(x-x₂)...(x-x_n-1)

  Многочлен p_n(x) степени n строится по узлам интерполяции x₀, x₁, x₂, ..., x_n, в которых он принимает значения y₀, y₁, y₂, ..., y_n; коэффициенты многочлена вычисляются последовательно по формуле

    a_n+1 = (y_n+1 - p_n(x_n+1)) / ((x_n+1 - x₀)(x_n+1 - x₁)...(x_n+1 - x_n))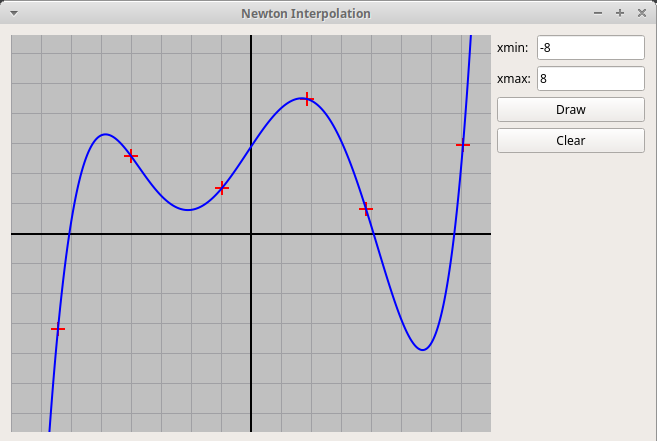
  

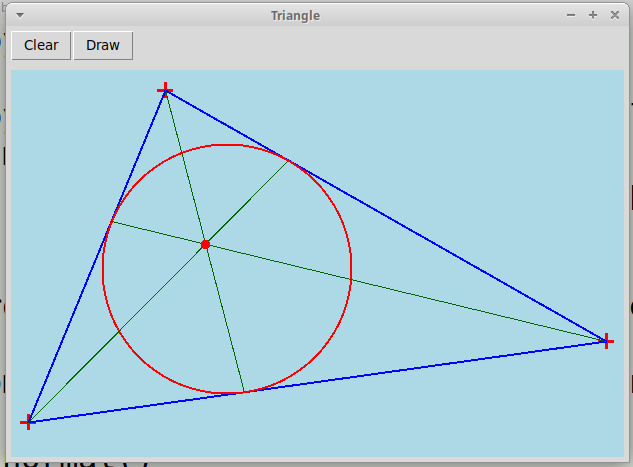
• Qt-проект "Треугольник": "Triangle.zip".
  По трем точкам, отмеченных кликами мыши, изображается треугольник, его три биссектрисы и вписанная окружность:
  
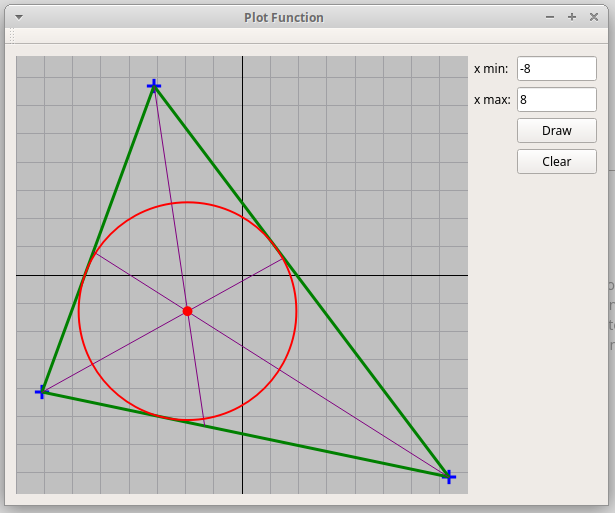
  Вершины треугольника можно перетаскивать мышью на новую позицию, при этом картинка изменяется в реальном времени.

Задачи на тему Qt

В задаче 1 надо использовать в качестве образца проект "График функции" PlotFunc.zip. В частности, следует использовать реализованный в нем парсер формул, который по формуле, зависящей от переменных x, y, получает ее обратную польскую запись; обратная польская запись формулы затем используется для вычисления значений формулы для конкретных численных значений переменных x, y. Формула может включать числовые константы, знаки арифметических операций, круглые скобки, стандартные математические функции (sin, cos, exp, log, atan, sqrt, ...), а также операцию возведения в степень ^.

В задачах 3-6 надо нарисовать треугольник, задаваемый кликами мыши, и одну из замечательных точек треугольника, определяемых как пересечение чевиан. Нарисовать надо не только саму точку (в виде маленького закрашенного кружка), но и процесс ее построения.

В качестве образца следует использовать Qt-проект "Triangle.zip".

Список задач

1. Задана функция f(x, y). (Функция задается в текстовом поле Qt-окна приложения, запись функции можно редактировать.) Нарисовать ее линию уровня (изогипсу), задаваемую уравнением f(x, y) = 0.
   Идея реализации. Разбиваем плоскость на маленькие треугольники. Для каждого треугольника вычисляем значение функции в его вершинах. Если значения одного знака, то линия не пересекает треугольник. Иначе имеем одну вершину одного знака и две вершины другого знака => используя линейную интерполяцию, вычисляем две точки на сторонах треугольника, в которых функция принимает значение 0. Получаем отрезок. Линии уровня состоят из этих отрезков.
2. Нарисовать кривую Безье, построенную по узлам, которые пользователь отмечает кликами мыши. Также реализовать возможность перетаскивания мышкой отмеченных раньше узлов на новую позицию, при этом уже построенная по этим узлам кривая Безье должна изменяться в реальном времени.

   Кривая Безье B(t) — это отображение числового отрезка [0, 1] в плоскость R²:

   B: [0, 1] → R²
   Кривая Безье порядка n задается n+1 узлом
   p₀, p₁, ..., p_n.
   Кривая нулевого порядка (построеная по одному узлу) — это просто точка. Кривая Безье B(t) порядка n, построенная по узлам p₀, p₁, ..., p_n, определяется рекурсивно через две кривые B₀(t) и B₁(t) порядка n-1; кривая B₀(t) строится по узлам
   p₀, p₁, ..., p_n-1,
   кривая B₁(t) — по узлам
   p₁, p₁, ..., p_n,
   Кривая Безье порядка n задается рекурсивно формулой:
   B(t) = B₀(t)·(1-t) + B₁(t)·t.

   На картинках ниже изображены кривые Безье, построенные по трем и четырем узлам:
   

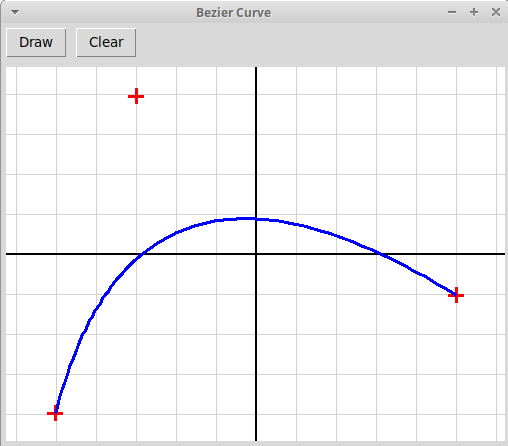
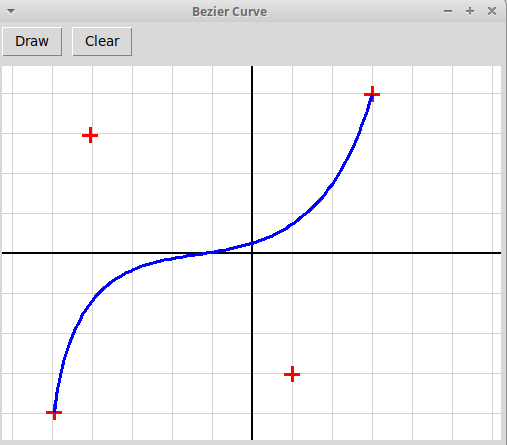
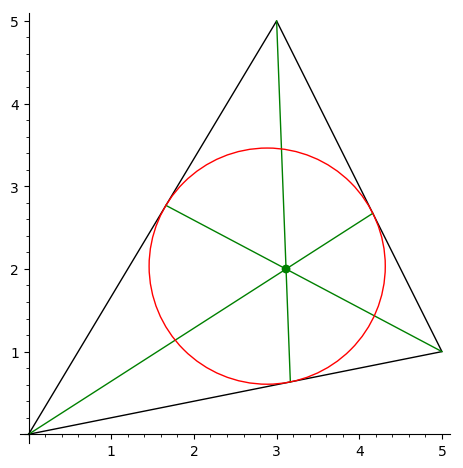
3. Нарисовать треугольник и точку Жергона — пересечение отрезков, соединяющих вершины треугольника с точками касания вписанной окружности.
   
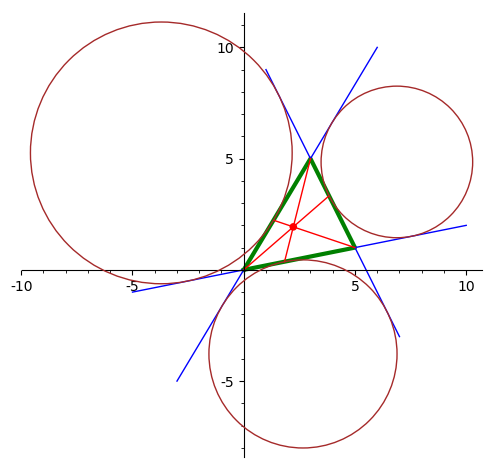
4. Нарисовать треугольник и точку Нагеля — пересечение отрезков, соединяющих вершины треугольника с точками касания трех внешне вписанных окружностей.
   
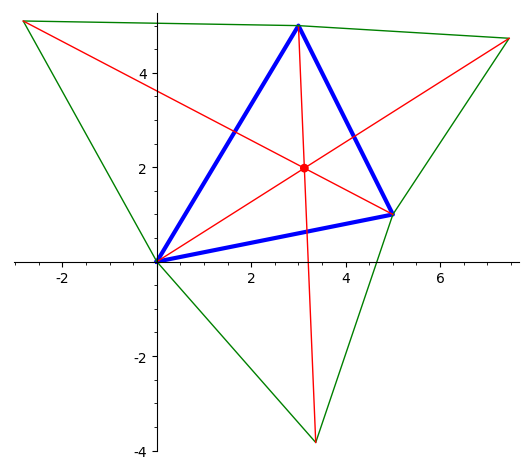
5. Нарисовать треугольник и точку Лемуана — точку, изогонально сопряженную центру тяжести треугольника. Она определяется как пересечение симмедиан. Симмедиана — это отрезок прямой, симметричной медиане треугольника относительно бисектриссы, проведенной из той же вершины.
   
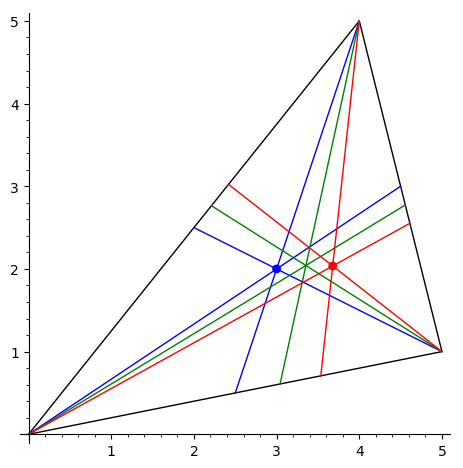
   На рисунке синяя точка — это пересечение медиан треугольника. Медианы изображены синим цветом, биссектрисы — зеленым, симмедианы — красным. Точка Лемуана изображена красным кружком.
6. Нарисовать треугольник и точку Ферма-Торричелли, а также процесс ее построения. Точка Ферма-Торричелли определяется как точка, сумма расстояний от которой до вершин треугольника минимальна. Если треугольник не тупоугольный или его тупой угол меньше 120 градусов, то это точка внутри треугольника, из которой каждая сторона видна под углом 120 градусов; иначе это вершина тупого угла.