Haskell & Python

Филиал МГУ в г. Душанбе

Факультет прикладной математики и информатики

Языки и методы программирования, 2021

Журнал группы ПМИ-3 (2020-21 уч.г.)

Содержание курса

Инсталляция для MS Windows

Haskell для 64-разрядной версии Windows:
HaskellPlatform-8.6.3-core-x86_64-setup.exe
Python
- Python для 32-разрядной версии Windows:
  python-3.7.2.exe
- Python для 64-разрядной версии Windows:
  python-3.7.2-amd64.exe

1. Haskell

Лучшая книга по Haskell:
Learn You a Haskell for Great Good!

Примерная программа лекций и семинаров по Haskell (2021 уч.г.)

Записи лекций по Haskell, январь 2021 г. (дистанционное обучение)

Примеры программ

Примеры вычислительных функций: calculations.hs
Алгоритмы теории чисел: numberTheory.hs
Модуль "Геометрия на плоскости": R2Graph.hs
Решение геометрических задач: geom.hs
Компилятор формул:
вариант без стандартных функций Rpn.hs
вариант со стандартными функциями RpnPlus.hs
консольная программа (main) rpnCalc.hs

Домашнее задание на 8 января 2021

Найти все совершенные числа в диапазоне [1..10000]. Число совершенное, если оно равно сумме всех своих собственных делителей, например
6 = 1 + 2 + 3,
28 = 1 + 2 + 4 + 7 + 14.
Найти все пифагоровы тройки, составленные из чисел, меньших 100. Тройка чисел (a, b, c) пифагорова, если числа a и b взаимно просты, gcd(a, b) = 1, и
a² + b² = c².

Домашнее задание на 11 января 2021

Вариант 1. Вычислить среднее геометрическое элементов положительной числовой последовательности.
Пример:
Последовательность [1,2,3,4], meanGeom = (1·2·3·4)^1/4 = 2.21336
Вариант 2. Вычислить среднее гармоническое элементов положительной числовой последовательности.
Пример:
Последовательность [1,2,3,4], meanHarm = 1/s, где s есть среднее значение обратных величин.

s = (1/1 + 1/2 + 1/3 + 1/4)/4
meanHarm = 1/s = 4/(1/1 + 1/2 + 1/3 + 1/4) = 48/25 = 1.92
Вы едете на автомобиле дистанцию в 100 км, первые 50 км со скоростью 50 км/ч, вторые 50 км со скоростью 100 км/ч. Средняя скорость на дистанции есть среднее гармоническое:
meanHarm = 2/(1/50 + 1/100) = 200/3 = 66.66666

Домашнее задание на 13 января 2021

Вариант 1. Найти делитель большого составного целого числа m, используя ρ-алгоритм Полларда (основан на поиске цикла в рекуррентной последовательности).
Вариант 2. Найти делитель большого составного целого числа m, используя p-1-алгоритм Полларда (основан на Малой теореме Ферма).
Вариант 3. Вычислить целую часть квадратного корня из целого числа неограниченной длины.
Указание. Самое простое решение методом деления пополам.
Вариант 4. Реализовать алгоритм для частного случая китайская теоремы об остатках при k=2.
Даны два взаимно простых числа p₁, p₂ и остатки r₁, r₂.
Найти x:
x ≡ r₁ (mod p₁),
x ≡ r₂ (mod p₂).

Домашнее задание на 18 января 2021

Задача 1. Варианты
1. Вычислить y = arcsin(x). (Свести вычисление функции к arctg(x) и sqrt(x), пользоваться библиотечными функциями нельзя.)
2. Вычислить y = arccos(x). (Свести вычисление функции к arctg(x) и sqrt(x), пользоваться библиотечными функциями нельзя.)
3. Вычислить y = x^α. (Свести вычисление функции к ln(x) и exp(x), пользоваться библиотечными функциями нельзя.)
Задача 2. Варианты
1. Вычислить окружность, описанную вокруг треугольника.
2. Вычислить точку пересечения высот треугольника (ортоцентр).
3. Вычислить точку Жергона треугольника.
  
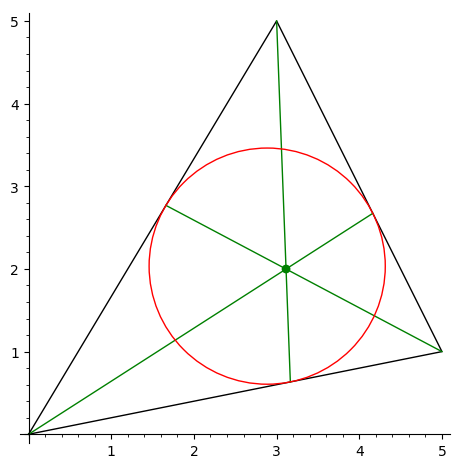
  Точка Жергона — это точка пересечения отрезков, соединяющих вершины треугольника с точками касания вписанной окружности.

Домашнее задание на 23 января, проект "Компилятор формул"

Компилятор формул:
вариант со стандартными функциями RpnPlus.hs,
консольная программа (main) rpnCalc.hs

Задачи по теме "Компилятор формул"

Добавить константы pi и e.
Помимо уже реализованных стандартных функций от одного аргумента, добавить стандартные функции от двух аргументов или трех аргументов: atan2(y, x), loga(a, x), powmod(x, y, z).
Добавить в язык операцию "унарный минус" (изменение знака числа), перед которой обязательно должна идти либо открывающая скобка, либо знак операции, например
```
    (-(2*3 + -5)*(-3/7 - 10))
    
```
Здесь первые три знака минус обозначают унарный минус, последний минус обозначает обычную операцию вычитания. Приоритет унарного минуса выше, чем умножения или деления, но ниже операции возведения в степень.

Лекция 1

Обзор алгоритмических языков. Процедурные и функциональные языки. Введение в Haskell

История алгоритмических языков. Классификация языков: традиционные (Fortran, C, Pascal, C++), объектно ориентированные (SmallTalk, Visual Basic, Eiffel, Java, C#, Python), функциональные (Refal, Prolog, Haskell).

Основы языка Haskell. Типы данных, функции, списки, умное задание списка (list comprehension), функция map. Рекурсия. Условное выражение "if... then... else" и гарды. Примеры программ: квадраты первых 20 натуральных чисел, 3 различные реализации этой программы; тест простоты, список простых чисел.

Самостоятельная работа

Вариант 1: найти все совершенные числа в диапазоне [1..10000]. Аналогичная (более сложная) задача для полусовершенных чисел. (Число называется совершенным, если оно равно сумме всех своих делителей, отличных от него самого; полусовершенным, если оно равно сумме некоторых своих делителей, не обязательно всех.)

Для нахождения полусовершенных чисел необходимо решить также задачу о рюкзаке: дан список положительных натуральных чисел (объемы вещей, которые надо поместить в рюкзак), а также натуральное число n (объем рюкзака). Можно ли составить из некоторого подмножества этих чисел сумму, в точности равную n (т.е. полностью заполнить рюкзак)?

Вариант 2: найти все пифагоровы тройки в диапазоне от 1 до 100. Тройка натуральных чисел (a, b, c) называется пиaфагоровой, если a² + b² = c² (т.е. числа a, b, c представляют собой длины сторон прямоугольного треугольника). Требуется также, чтобы числа a, b, c были упорядочены, т.е. a ≤ b, а также взаимно просты: gcd(a, b) = 1.

Примеры программ

Напечатать квадраты первых 20 натуральных чисел

square :: Int -> Int
square x = x*x

smallNumbers :: [Int]
smallNumbers = [1..20]

squares :: [(Int,Int)]
squares = zip smallNumbers (map square smallNumbers)

main :: IO()
main = putStrLn (show squares)

Работая в интерпретаторе ghci, мы можем просто напечатать:

Prelude> map (\ x -> x^2) [1..20]

получим


[1,4,9,16,25,36,49,64,81,100,121,144,169,196,225,256,289,324,361,400]

Здесь мы используем лямбда-функцию

    (\ x -> x^2)

которая отображает каждый элемент списка [1..20] на его квадрат.

Если мы хотим получить список пар (число, квадрат числа), то можно использовать функцию zip, которая подобно застежке-молнии соединяет два списка одинаковой длины в один список, состоящий из пар:

Prelude> zip [1..20] (map (\ x -> x^2) [1..20])

Получаем:

[(1,1),(2,4),(3,9),(4,16),(5,25),(6,36),(7,49),(8,64),
(9,81),(10,100),(11,121),(12,144),(13,169),(14,196),
(15,225),(16,256),(17,289),(18,324),(19,361),(20,400)]

Но наиболее элегантное решение получается при использовании умного задания списка (list comprehension):

Prelude> [(n, n^2) | n <- [1..20]]

Еще один пример, использующий list comprehension: получить все числа в диапазоне [1..29], которые не делятся на 2, 3, 5 (такие числа используются в алгоритме разложения числа на множители "Колесо" и играют роль спиц колеса, которое катится по числовой оси).

Prelude> [n | n <- [1..29], n `mod` 2 /= 0, n `mod` 3 /= 0, n `mod` 5 /= 0]

Получим:

[1,7,11,13,17,19,23,29]

Тест простоты

Самый тривиальный тест простоты нечетного натурального числа n состоит в проверке того, что число не делится на нечетные пробные делители, квадрат которых не превосходит n. Все такие пробные делители составляют список:

    [d | d <- [3, 5..n-1], d^2 <= n]

Мы будем использовать также вспомогательную функцию divisible n divisors, где n — целое число, которое мы проверяем, а divisors — список пробных делителей. Функция возвращает значение True тогда и только тогда, когда n делится на один из пробных делителей списка. Реализация функции использует рекурсию:

divisible :: Int->[Int]->Bool
divisible x y =
    if y == []
    then False
    else if x `mod` (head y) == 0
         then True
         else divisible x (tail y)

Здесь используется конструкция условного выражения "if ... then ... else ... ". Но при помощи гардов она записывается гораздо более элегантно:

divisible :: Int->[Int]->Bool
divisible x y
    | y == []               = False
    | x `mod` (head y) == 0 = True
    | otherwise             = divisible x (tail y)

Используя эту вспомогательную функцию и гарды, мы легко реализуем тест простоты:

prime :: Int->Bool
prime n
    | n < 2     = False
    | n == 2    = True
    | even n    = False
    | otherwise =
      not (divisible n [3,5..n-2])

С помощью теста простоты можно найти, например, все простые числа, не превышающие числа 100:

Prelude> [n | n <- [1..100], prime n]

Получим:

[2,3,5,7,11,13,17,19,23,29,31,37,
41,43,47,53,59,61,67,71,73,79,83,89,97]

Или найдем, например, 10 максимальных простых чисел, не превышающих миллиона:

Prelude> take 10 [n | n <- [999999, 999997..], prime n]

Получим:

[999983,999979,999961,999959,999953,999931,999917,
999907,999883,999863]

Лекция 2

Классы типов, сигнатура функций, сопоставление с образцами (Pattern Matching) в Haskell

Классы типов и сигнатура функций. Сопоставление с образцами (pattern matching) и его использование при задании функций. Комбинация сопоставления с образцом и гардов. Применение рекурсии при работе со списками. Реализация некоторых математических алгоритмов: обычный и расширенный алгоритмы Евклида. Конструкция "let ... in ...".

Контрольная работа, 4 варианта:

1. Вычислить значение многочлена в заданной точке. Коэффициенты многочлена заданы в списке по убыванию степеней. Считается, что нулевому многочлену соответствует пустой список.

2. Вычислить значение многочлена в заданной точке. Коэффициенты многочлена заданы в списке по возрастанию степеней. Считается, что нулевому многочлену соответствует пустой список.

3. Вычислить производную многочлена. Коэффициенты многочлена и его производной задаются в списке по возрастанию степеней. Результатом функции должен быть список коэффициентов производной многочлена по возрастанию степеней. Считается, что нулевому многочлену соответствует пустой список.

4. Вычислить первообразную многочлена (неопределенный интеграл). Коэффициенты многочлена и его первообразной задаются в списке по возрастанию степеней. Результатом функции должен быть список коэффициентов первообразной многочлена по возрастанию степеней.

Примеры программ

Алгоритм Евклида

Даны 2 целых числа, хотя бы одно из которых отлично от нуля. Нужно вычислить их наибольший общий делитель. Мы используем название myGcd для нашей функции, поскольку функция gcd является стандартной и представлена в модуле Prelude. Вот реализация функции myGcd:

myGcd :: (Integral a) => a->a->a
myGcd x 0 = x
myGcd x y = myGcd y (x `mod` y)

Первая строка в определении функции задает ее сигнатуру (type signature), т.е. описывает тип функции и ее формальных параметров. Здесь буквой a обозначен класс типа (type class), а часть строки в круглых скобках представляет собой ограничение на класс типа (type constrain). Оно означает, что тип a должен представлять собой один из целочисленных (Integral) типов. Это может быть либо ограниченное целое число (тип Int), либо неограниченное (тип Integer) — оба этих типа принадлежат к классу типов Integral. Часть первой строки после символов => задает типы формальных параметров и возвращаемого значения функции, в данном случае это один и тот же тип a.

Тело функции использует сопоставление с образцами (pattern matching). Первый образец "x 0" означает, что второй параметр функции равен нулю. В этом случае наибольший общий делитель равен первому параметру x:

myGcd x 0 = x

Если сопоставление с первым образцом не проходит, то мы используем уже образец общего вида "x y", причем мы уже знаем, что второй параметр y отличен от нуля (поскольку сопоставление с образцами выполняется сверху вниз и сопоставление с первым образцом не состоялось). Для такой пары

    gcd(x, y) = gcd(y, r),

где r — остаток от деления x на y; остаток r вычисляется с помощью операции `mod`:

    r = x `mod` y.

Таким образом, рекурсивное применение функции myGcd к паре (y, x `mod` y) решает нашу задачу:

myGcd x y = myGcd y (x `mod` y)

Расширенный алгоритм Евклида

Расширенный алгоритм Евклида чрезвычайно важен для различных приложений теории чисел, в частности, для криптографии. Даны два целых числа m и n, хотя бы одно из которых отлично от нуля. Требуется найти их наибольший общий делитель d, а также его выражение в виде линейной комбинации исходных чисел m и n с целочисленными коэффициентами u и v: d = u·m + v·n Идея реализации расширенного алгоритма Евклида такая же, как в обычном алгоритме Евклида: мы заменяем пару (m, n) на пару (n, r), где r — остаток от деления m на n: m = q·n + r,    |r| < |n|. При этом наибольший общий делитель пары остается неизменным. Для пары (m, 0) коэффициенты u, v и наибольший общий делитель легко вычисляются: d = m,    m = 1·m + 0·n,
u = 1,   v = 0. А зная выражение наибольшего общего делителя d в виде линейной комбинации пары (n, r), легко вычислить выражение d в виде линейной комбинации исходной пары, подставив выражение r через m и n: d = u'·n + v'·r,    r = m - q·n,
d = u'·n + v'·(m - q·n) = v'·m + (u' - v'·q)·n,
u = v',    v = u' - v'·q.

Ниже приведена реализация расширенного алгоритма Евклида на языке Haskell — это функция extGcd. На вход ей подаются два числа m и n, на выходе она возвращает тройку (d, u, v):

extGcd :: (Integral a) => a->a->(a, a, a)
extGcd m 0 = (m, 1, 0)
extGcd m n =
    let 
        q = m `div` n; r = m `mod` n
        (d, u', v') = extGcd n r
        u = v'; v = u' - v'*q
    in
        (d, u, v)

Оба алгоритма Евклида содержатся в файле "myGcd.hs".

Примеры задач на работу со списками: "lists.hs".

Лекция 3

Хвостовая рекурсия (tail recursion)

Проблема с применением обычной (иногда говорят, наивной) рекурсии состоит в возможном переполнении стека. Рассмотрим, например, список длиной в миллион. Если использовать наивную рекурсию для реализации какой-нибудь функции, работающий с этим списком, то при ее исполнении понадобится стек размером 1000000·размер стекового фрейма, содержащего локальные переменные и адрес возврата. Поскольку стандартный размер стека 4 мегабайта (значение по умолчанию для многих компиляторов и алгоритмических языков), то очень вероятно переполнение стека, что означает катастрофу.

Но при использовании хвостовой рекурсии (tail recursion) большинство компиляторов могут применять оптимизацию вызовов функций, при которой глубина стека ограничивается небольшим размером независимо от формальной глубины рекурсии. (Стековый фрейм вызывающей функции может быть освобожден в момент рекурсивного вызова функции, поскольку при хвостовой рекурсии никаких дальнейших действий в вызывающей функции не требуется, так что можно вообще в нее не возвращаться.) Более того, хвостовая рекурсия работает быстрее и зачастую выглядит естественнее и проще наивной рекурсии, если привыкнуть к ее использованию. В каком-то смысле она соответствует циклу while — можно сформулировать простой рецепт, как программу, использующую цикл while, переделать в программу, применяющую вместо него хвостовую рекурсию. Поскольку в функциональных языках, в частности в Haskell, никаких циклов нет, хвостовая рекурсия в них являтся основным приемом программирования.

Не так-то просто дать точное и строгое определение хвостовой рекурсии. Формально рекурсия является хвостовой, если рекурсивный вызов функции является последним выполняемым в ней действием. При этом возвращаемое значение вызывающей функции совпадает с возвращаемым значением вызываемой при рекурсивном вызове функции. Это означает, что возврат в вызывающую функцию вообще не требуется, возвращаемое значение может быть выдано напрямую из вызываемой функции.

Очень часто при хвостовой рекурсии используется значение аккумулятора (одной переменной или набора переменных), в котором накапливается результат при серии рекурсивных вызовов. Поэтому вместо термина "хвостовая рекурсия" зачастую используется название "рекурсия с аккумулятором".

Рассмотрим простейший пример вычисления факториала целого неотрицательного числа. Напишем сначала функцию на языке C, использующую наивную рекурсию:

    int factorial(int n) {
        if (n == 0) {
            return 1;
        } else {
            return n*factorial(n - 1);
        }
    }

Здесь рекурсия не является хвостовой, поскольку рекурсивный вызов factorial(n - 1) не является последним действием: после завершения рекурсивного вызова нужно еще умножить его результат на n. Поэтому стек вызывающей функции не может быть освобожден в момент рекурсивного вызова.

Как переделать эту функцию, чтобы рекурсия стала хвостовой? Добавим еще один дополнительный параметр, который обычно называют аккумулятором. Смысл аккумулятора состоит в том, что он как бы накапливает частичный результат при серии рекурсивных вызовов. Когда мы уже обработали часть входных данных, аккумулятор содержит значение функции для обработанной части. Вместо одной функции factorial нам понадобятся две функции: в дополнение к ней мы используем также вспомогательную функцию factorial0 с дополнительным параметром acc. Основная функция factorial просто вызывает вспомогательную функцию factorial0, передавая ей начальное значение аккумулятора (1 для факториала). При этом функция factorial никакой рекурсии не использует и вообще перекладывает всю свою работу на плечи вспомогательной функции factorial0.

Вспомогательная функции factorial0 реализована с помощью хвостовой рекурсии. Она вызывается со значением аккумулятора, в котором уже хранится результат для обработанной части данных, также ей передается необработанная часть. Если необработанная часть данных уже пустая, то функция просто возвращает значение аккумулятора. Иначе функция берет очередную порцию данных, обрабатывает ее и добавляет каким-либо образом к аккумулятору — в случае факториала для этого используется умножение. Затем функция рекурсивно вызывает саму себя, передавая новое значение аккумулятора и оставшуюся часть данных. Вычисленное при рекурсивном вызове значение возвращается как результат функции без всякой дополнительной обработки.

    int factorial(int n);                  // Global function
    static int factorial0(int acc, int n); // Auxiliary function

    int factorial(int n) {
        return factorial0(1, n);
    }

    static int factorial0(int acc, int n) {
        if (n <= 1) {
            return acc;
        } else {
            return factorial0(acc*n, n - 1);
        }
    }

Запишем эти функции на языке Haskell:

    factorial :: Integral a => a->a
    factorial n = factorial' 1 n

    factorial' :: Integral a => a->a->a
    factorial' acc n
        | n <= 1        = acc
        | otherwise     = factorial' (acc*n) (n - 1)

Применение хвостовой рекурсии для обработки списков

Хвостовая рекурсия очень полезна при работе со списками. Рассмотрим, например, задачу вычисления значения многочлена в заданной точке, когда коэффициенты многочлена заданы в списке по убыванию степеней. Идея реализации функции состоит в применении схемы Горнера. Рассмотрим многочлен степени n p_n = a₀ xⁿ + a₁ x^n-1 + ... + a_n Обозначим через p_n+1 полином степени на единицу выше, который получается добавлением еще одного коэффициента a_n+1 в конец списка коэффициентов: p_n+1 = a₀ xⁿ⁺¹ + a₁ xⁿ + ... + a_n x + a_n+1 Тогда справедливо соотношение: p_n+1 = p_n x + a_n+1. Оно дает возможность вычислить значение многочлена в точке, используя хвостовую рекурсию. Аккумулятором в данном случае является значение многочлена меньшей степени, соответствующего обработанной начальной части списка коэффициентов:

    polvalue :: Num a => [a]->a->a
    polvalue coeffs x = polvalue' 0 coeffs x

    polvalue' :: Num a => a->[a]->a->a
    polvalue' acc [] x = acc
    polvalue' acc (h:t) x = polvalue' (acc*x + h) t x

В последней строке шаблон (h:t) разбивает необработанную часть списка коэффициентов многочлена на первый необработанный коэффициент h и список остальных коэффициентов t. Отделив первый необработанный коэффициент, мы вычисляем новое значение аккумулятора по схеме Горнера:

    acc*x + h

Когда необработанная часть списка коэффициентов станет пустой, аккумулятор будет содержать значение многочлена в точке x.

Лекция 4

Разбор текста. Парсер арифметических формул, использующий преобразование в обратную польскую запись (Reverse Polish Notation)

Рассматривается реализация компилятора арифметических формул на языке Haskell. Компиляция выполняется в 2 этапа: лексический анализ выполняется сканером, затем выход сканера подается на вход парсеру, который выполняет синтаксический анализ и генерацию кода. Сканер разбивает входную строку символов на список лексем. Лексемы (тип Token) представляют собой объекты, содержащие 3 поля:
1) тип лексемы (представляется перечислимым типом Lexeme) — это 5 знаков арифметических операций, включая возведение в степень, открывающая и закрывающая скобки, имя функции, численная константа, неравильная лексема;
2) ее текст (тип String);
3) ее численное значение (тип Double), которое используется для численных констант.
Вот как описываются эти типы:

data Lexeme = Number | Name | 
              Plus | Minus | Mul | Div | Power |
              LPar | RPar | EndLine | Illegal
              deriving (Eq, Ord, Show)

data Token = Token {
    lexeme :: Lexeme,
    text :: String,
    value :: Double
} deriving (Show, Eq, Ord)

Работу сканера выполняет функция scanner, которая получает на вход текстовую строку, разбивает ее на лексемы и на выходе выдает список лексем. Ее реализация использует хвостовую рекурсию с аккумулятором:

scanner :: String -> [Token]
scanner str = scanner' [] str

scanner' :: [Token] -> String -> [Token]
scanner' acc "" = reverse acc
scanner' acc str =
    let (token, rest) = spanToken str
    in
    if (lexeme token) == EndLine then reverse acc
    else scanner' (token:acc) rest

Реализация функции scanner основана на использовании функции spanToken, которая выделяет одну лексему из начала списка символов и возвращает пару (tuple), состоящую из выделенной лексемы и оставшейся части списка.

spanToken :: String -> (Token, String)
spanToken "" = (Token EndLine "" 0, "")
spanToken str@(h:t)
    | isSpace h         =
      let (u, v) = span isSpace str
      in spanToken v
    | otherwise         =
      if h == '+' then (Token Plus [h] 0, t)
      else if h == '-' then (Token Minus [h] 0, t)
      else if h == '*' then (Token Mul [h] 0, t)
      else if h == '/' then (Token Div [h] 0, t)
      else if h == '^' then (Token Power [h] 0, t)
      else if h == '(' then (Token LPar [h] 0, t)
      else if h == ')' then (Token RPar [h] 0, t)
      else if isAlpha h then
          let (u, v) = span isAlphaNum str
          in (Token Name u 0, v)
      else if isDigit h then
          let (u, v) = span (\ c -> isDigit c || c == '.') str
              n = read u::Double
          in (Token Number u n, v)
      else (Token Illegal "Illegal" 0, t)

Парсер преобразует список лексем (типа Token) в обратную польскую запись лексем того же типа. Он применяет алгоритм Дийкстры, который носит название "Сортировочная станция" (shunting-yard algorithm). В нем используется выходной список, а также стек отложенных операций и круглых скобок. Основная функция, реализующая работу парсера, называется parserRPN:

parserRPN :: [Token] -> [Token]
parserRPN tokens = parserRPN' ([], []) tokens

Ее реализация также основана на идее хвостовой рекурсии (она применяется во вспомогательной функции parserRPN') и использовании аккумулятора. В роли аккумулятора выступает пара (tuple) списков, первый из который представляет выходной список, второй — список отложенных операций.

. . .

Реализация сканера и парсера — модуль Rpn: "Rpn.hs".

Интерфейс с пользователем (грязный код) — функция main: "rpnCalc.hs".

2. Python

Журнал группы ПМИ-3 (2020-21 уч.г.)

Записи лекций по Питону, март-апрель 2021 г.

Лекция 5

Введение в Python

Место Python'а среди языков программирования: объектно ориентированный язык с некоторыми чертами функциональных языков (работа со списками, лямбда-функции и т.п.). Это объектно ориентированный язык в строгом смысле (в отличие, например, от языка С++, который занимает промежуточное положение между традиционными и объектно ориентированными языками). Python — язык с динамической типизацией: переменные в Python'е не имеют типов и хранят ссылки на объекты, которые находятся в управляемой динамической памяти. Тип выражения определяется не по переменным, а по объектам, на которые ссылаются переменные. Таким образом, тип выражения в Python'е невозможно определить статически, по тексту программы, он определяется только в процессе выполнения программы.

Некоторые замечательные черты языка Python: он поддерживает работу с неограниченными целыми числами; в нем есть очень удобный цикл for; имеется элегантный способ определения списков (и их содержимого), который называется "list comprehension", что можно перевести на русский как "умное, или математическое определение списка". Можно не только выполнять программы на Python'е, но и запускать Python в режиме интерпретатора. Это позволяет использовать Python как быстрый и удобный калькулятор с практически неограниченными возможностями.

Примеры программ, файл prime.py:

вычисление наибольшего общего делителя целых чисел, функция gcd(a, b);
несложный тест проверки простоты, функция prime(m);
несложный алгоритм факторизации целого числа, функция factor(m);
проверка, является ли число совершенным, т.е. равно ли оно сумме своих собственных делителей, функция perfect(m);
получение списка и числа счастливых билетов длины n (n четное), функции happy(number), happyTickets(n), numHappyTickets(n).

Домашнее задание 1

В задании 3 варианта, нужно сделать одну задачу — ту, номер которой совпадает по модулю 3 с номером студента в журнале.

Реализовать функцию knapsack(lst, m), которая решает задачу о рюкзаке. Дан список положительных целых чисел lst (объемы вещей) и неотрицательное целое число m (объем рюкзака). Можно ли найти подмножество s списка lst такое, что сумма его элементов в точности равна m? Функция должна возвращать пару (False, []), если нельзя, и пару (True, s), если можно; при этом список s состоит из элементов исходного списка, сумма которых в точности равна m (список s представляет подмножество вещей, которые мы сложили в рюкзак, чтобы его заполнить полностью).
С помощью функции knapsack(lst, m) реализовать также функцию semiperfect(m), проверяющую, является ли число m полусовершенным, т.е. равно ли оно сумме некоторого подмножества своих собственных делителей.
Написать более быструю реализацию функции numHappyTickets(n), вычисляющей число счастливых билетов длины n, где n — четное число. Номер билета счастливый, если сумма первой половины его цифр равна сумме второй половины.
Пусть список p целых чисел от 1 до n представляет перестановку порядка n, например, p = [2, 3, 4, 1]. Реализовать функцию nexPermutation(p), которая заменяет содержимое этого списка на следующую перестановку в лексикографическом порядке. Например, для указанной перестановки следующей будет [2, 4, 1, 3]. Функция должна возвращать True, если мы дошли до конца (т.е. текущая перестановка является последней в лексикографическом порядке), или False в противном случае.

Работа с матрицами в Python'е

Матрица в Питоне обычно представляется списком строк, где каждая строк — это список чисел. Например,

    >>> a = [[1, 2, 3], [4, 5, 6], [7, 8, 0]]
    >>> print(a)
    [[1, 2, 3], [4, 5, 6], [7, 8, 0]]

Замечательная особенность Питона состоит в том, что в нем реализованы целые числа неограничеснного размера. Это позволяет реализовать также и рациональные числа. Реализация рациональных чисел с помощью целых чисел типа int или long long в языке C++ бессмысленна, т.к. при арифметических действиях с рациональными числами их знаменатели растут очень быстро, и почти сразу наступает переполнение. В Питоне переполнений не бывает. Рациональные числа представлены в Питоне классом Fraction в модуле fractions:

    >>> from fractions import *
    >>> a = Fraction(1, 3)
    >>> print(a)
    1/3
    >>> b = Fraction(1, 4)
    >>> print(b)
    1/4
    >>> print(a + b)
    7/12

Рациональные числа типа Fraction позволяют использовать точную арифметику и получать точный результат, в отличие от вещественных чисел типа float. Например, для типа float бессмыслено сравнивать числа на точное равенство, результат непредсказуем:

    >>> a = 1/3
    >>> a
    0.3333333333333333
    >>> b = 1/4
    >>> b
    0.25
    >>> a + b
    0.5833333333333333
    >>> 7/12
    0.5833333333333334
    >>> 1/3 + 1/4 == 7/12
    False

Неожиданный результат! Для вещественных чисел, представленных типом float, сумма 1/3 + 1/4 не равна 7/12 (отличие мизерное, но точного равенства нет).

Для матриц над полем рациональных чисел в Питоне можно реализовать метод Гаусса приведения матрицы к ступенчатому в точности так, как этот метод рассматривается в курсе математики. Это позволяет с помощью программ на Питоне решать задачи, которые обычно даются первокурсникам на практических занятиях в курсе алгебры или линейной алгебры: приведение матрицы к ступенчатому виду, вычисление определителя матрицы, решение систем линейных уравнений, вычисление обратной матрицы и т.п.

Отметим, что для матриц из вещественных чисел метод Гаусса имеет свои особенности: во-первых, мы не можем просто считать элемент равным нулю, поскольку точных равенств при работе с элементами типа float не бывает! Поэтому мы считаем элемент матрицы нулевым, если его абсолютная выличина не превосходит маленького числа eps, например, eps = 1e-8:

    >>> (1/3 + 1/4) - 7/12 == 0
    False
    >>> abs((1/3 + 1/4) - 7/12) <= eps
    True

Во-вторых, в методе Гаусса при приведении матрицы к ступенчатому виду нельзя выбирать произвольный ненулевой разрешающий элемент в столбце. Если мы выберем маленький ненулевой элемент, то при делении на него строка в результате будет умножаться на очень большое число, что приводит к экспоненциальному росту ошибок и неустойчивости алгоритма. В результате такого алгоритма вместо правильного (или близкого к правильному) ответа мы будем получать просто мусор! Надо обязательно выбирать элемент, максимальный по абсолютной величине в столбце, чтобы при делении на него строка умножалась на коэффициент, не превосходящий единицы.

В файле matrix.py реализована работа с матрицами на полем рациональных чисел (тип Fraction) и над полем вещественных чисел (тип float). Функция echelonFormOfRationalMatrix(a) приводит матрицу рациональных чисел к ступенчатому виду и возвращает пару (ступенчатый вид матрицы, ранг матрицы), при этом сама матрица a не изменяется (действия производятся с копией матрицы). Функция showRationalMatrix(a) преобразует объект "матрица" к текстовому виду так, чтобы потом матрицу можно было красиво напечатать:

    >>> from matrix import *
    >>> a = [[1, 2, 3], [4, 5, 6], [7, 8, 0]]
    >>> print(showRationalMatrix(a))
    [1 2 3]
    [4 5 6]
    [7 8 0]
    >>> (b, rank) = echelonFormOfRationalMatrix(a)
    >>> print(showRationalMatrix(b))
    [ 1  2  3]
    [ 0 -3 -6]
    [ 0  0 -9]

Аналогичные функции echelonFormOfRealMatrix(a) и showRealMatrix(a) реализованы для вещественных матриц:

    >>> a = [[1, 2, 3], [4, 5, 6], [7, 8, 0]]
    >>> (b, rank) = echelonFormOfRealMatrix(a)
    >>> print(showRealMatrix(b))
    [     -7.0000      -8.0000      -0.0000]
    [     -0.0000      -0.8571      -3.0000]
    [      0.0000       0.0000       4.5000]

Кроме того, в модуле matrix.py реализованы функции вычисления определителя матрицы, умножения матриц, а также выполнение элементарных преобразований и копирование матриц.

Домашнее задание 2

В задании 4 варианта, нужно сделать одну задачу — ту, номер которой совпадает по модулю 4 с номером студента в журнале. Во всех задачах надо реализовать функцию, которая в зависимости от варианта возвращает либо матрицу, либо линейный массив. Реализованную функцию надо добавить в файл matrix.py.

Отметим еще раз, что функция не должна ничего печатать (и уж тем более не должна ничего вводить с клавиатуры!). Результатом работы функции должно быть вычисление требуемого объекта, который функция должна возвращать с помощью оператора return. Исходные аргументы функции при этом меняться не должны.

Вычислить обратную матрицу к невырожденной квадратной рациональной матрице:
```
    b = inverseRationalMatrix(a)
```
Вычислить обратную матрицу к невырожденной квадратной вещественной матрице:
```
    b = inverseRealMatrix(a)
```
Решить систему линейных уравнений с невырожденной квадратной рациональной матрицей:
```
    x = solveRationalSystem(a, b)
```
Здесь a — матрица рациональных чисел, b — массив свободных членов уравнений. Функция должна вернуть массив x рациональных чисел, представляющий решение системы a*x = b.
Решить систему линейных уравнений с невырожденной квадратной вещественной матрицей:
```
    x = solveRealSystem(a, b)
```
Здесь a — матрица вещественных чисел, b — массив свободных членов уравнений. Функция должна вернуть массив x рациональных чисел, представляющий решение системы a*x = b.

Лекция 6

Классы в языке Python

Прежде чем учиться писать свои собственные классы, давайте попробуем воспользоваться уже готовыми классами для решения задач. Рассмотрим геометрические задачи на плоскости R², например, задачи на нахождение замечательных точек треугольника (центры вписанной и описанной окружностей, ортоцентр, точки Жергона, Нагеля, Лемуана, точка Ферма-Торричелли и т.п.). Все подобные задачи решаются легко и изящно, если использовать классы R2Vector и R2Point, реализующие вектор и точку на плоскости. Эти классы определены в модуле "R2Graph.py". Главная идея состоит в том, чтобы использовать методы этих классов вместо манипуляций с координатами векторов и точек, характерных для аналитической геометрии. Поскольку методы этих классов имеют ясный геометрический смысл, решение задач становится простым и геометрически наглядным, что значительно сокращает текст программы и уменьшает вероятность ошибок.

Операции с векторами и точками

Пусть даны два вектора u, v, например

    from R2Graph import *
    u = R2Vector(1, 2)
    v = R2Vector(3, -4)

С векторами возможны следующие операции:

сложение и вычитание векторов

    >>> u + v
    R2Vector(4.0, -2.0)
    >>> u - v
    R2Vector(-2.0, 6.0)

умножение вектора на число
```
    >>> u*0.75
    R2Vector(0.75, 1.5)
```
скалярное произведение двух векторов (dot product)
```
    >>> u*v
    -5.0
```

длина, или норма вектора (синонимы):

    >>> u = R2Vector(1, 2)
    >>> u.norm()
    2.23606797749979
    >>> u.length()
    2.23606797749979

нормаль к вектору v — это вектор n той же длины, который получается из вектора v поворотом на 90 градусов против часовой стрелки. Если вектор v имеет координаты (x, y), то вектор n имеет координаты (-y, x).
```
     >>> v
     R2Vector(3.0, -4.0)
     >>> n = v.normal()
     >>> n
     R2Vector(4.0, 3.0)
```
метод u.normalized() возвращает нормализованную форму вектора u, т.е. вектор единичной длины того же направления, что и вектор u (сам вектор u при этом не меняется):
```
    >>> u
    R2Vector(1.0, 2.0)
    >>> w = u.normalized()
    >>> w
    R2Vector(0.4472135954999579, 0.8944271909999159)
```
метод u.normalize() нормализует вектор u, т.е. умножает его на число, обратное длине вектора (при этом вектор u меняется):
```
    >>> u
    R2Vector(1.0, 2.0)
    >>> u.normalize()
    R2Vector(0.4472135954999579, 0.8944271909999159)
    >>> u
    R2Vector(0.4472135954999579, 0.8944271909999159)
```

Класс R2Point реализует точку на плоскости. Разность двух точек является вектором, направленным от второй к первой точке:

    >>> p1 = R2Point(1, 2)
    >>> p2 = R2Point(3, -4)
    >>> p1 - p2
    R2Vector(-2.0, 6.0)

К точке можно прибавить или от нее отнять вектор, получим точку, сдвинутую на указанный вектор:

    >>> p1 + R2Vector(10, 20)
    R2Point(11.0, 22.0)

Расстояние между точками p1 и p2 можно найти с помощью метода distance:

    >>> p1 = R2Point(0, 0)
    >>> p2 = R2Point(1, 1)
    >>> d = p1.distance(p2)
    >>> d
    1.4142135623730951

Расстояние от точки t до прямой, заданной точкой p и направляющим вектором v, вычисляется с помощью метода distanceToLine:

    >>> t = R2Point(1, 1)
    >>> p = R2Point(0, 1)
    >>> v = R2Vector(1, -1)
    >>> d = t.distanceToLine(p, v)
    >>> d
    0.7071067811865475

Наконец, в модуле "R2Graph.py" имеется функция intersectLines, вычисляющая точку пересечения двух прямых. Каждая из прямых задается точкой и направляющим вектором. Функция возвращает пару (intersected, q), где intersected — логическое значение, равное True, если прямые не параллельны, в этом случае q — это точка пересечения прямых. Если прямые параллельны, то функция возвращает пару (False, None):

    >>> p1 = R2Point(0, 2)
    >>> v1 = R2Vector(1, 0)
    >>> p2 = R2Point(0, 0)
    >>> v2 = R2Vector(3, 1)
    >>> intersectLines(p1, v1, p2, v2)
    (True, R2Point(6.0, 2.0))
    >>> intersectLines(p1, v1, p2, v1)
    (False, None)

Домашнее задание 4

В задании 3 варианта, нужно сделать одну задачу — ту, номер которой совпадает по модулю 3 с номером студента в журнале. Во всех задачах надо реализовать функцию, которая возвращает требуемый объект. Функция не должна ничего печатать (и уж тем более не должна ничего вводить с клавиатуры!).

Функция должна использовать классы R2Point, R2Vector и их методы, имеющие геометрический смысл. При этом запрещено использовать координаты векторов и точек и вычисления с ними: требуется привести решение чисто в объектно ориентированного стиле. Для использования этих классов нужно импортировать модуль "R2Graph.py".

В качестве образца дается реализация функции, которая находит окружность, вписанную в треугольник: файл "triang.py". В программе реализована функция

    (center, radius) = inscribedCircle(a, b, c)

аргументами которой являются вершины треугольника (объекты типа R2Point), возвращающая пару, содержащую центр и радиус вписанной окружности.

Список задач

Реализовать функцию, вычисляющую окружность, описанную вокруг треугольника:
```
    (center, radius) = circumCircle(a, b, c)
```
Реализовать функцию, вычисляющую точку пересения высот треугольника (ортоцентр):
```
    o = orthocenter(a, b, c)
```
Реализовать функцию, вычисляющую точку Жергона треугольника:
```
    p = gergonnePoint(a, b, c)
```
Точка Жергона — это точка пересечения отрезков, соединяющих вершины треугольника с точками касания вписанной окружности и сторон треугольника:

Конструирование собственных классов в Python'е

Домашнее задание 5

1. Реализовать класс Треугольник на плоскости
class Triangle:
Методы:
    -- конструктор (даются 3 точки в общем положении)
    -- __getitem__, __setitem__ (работа с треугольником как с массивом
                                 из 3-х элементов)
    -- периметр
    -- площадь со знаком
    -- площадь
    -- ориентация (+1 если CCW, -1 CW)
    -- centroid (центр тяжести)
    -- точка внутри треугольника: True/False
    -- ориентировать (если он отрицательно ориентирован, то изменить
                      порядок вершин)
                      
2. Реализовать афинное преобразование плоскости.
        Transform
    Любое аффинное преобразование есть композиция 
    линейного преобразования и сдвига
        transform(p) = a*p + b
    где a -- невырожденная матрица размера 2x2, 
             задающая линейное преобразование,
        b -- вектор сдвига    

    -- конструктор, 2 варианта:
            1) задается матрица a и R2Vector b;
            2) задаются два треугольника t1 и t2, определяющие
               афинное преобразование: t1 --> t2
    -- произведение (композиция) преобразований
    -- вычислить обратное преобразование
    -- действие преобразования на точку
           p2 = t*p1
       где t -- афинное преобразование, p1 -- исходная точка,
                                        p2 -- ее образ под действием t.
                                        
3. Реализовать класс "вещественное число с фиксированной точкой",
    FixedReal
   которое представляется в виде
       m*10^(-k), 
   m -- целое число (мантисса), k -- количество десятичных
                                     цифр после десятичной точки.
   Число k фиксировано, это статический член класса.
Например, если k = 3, то числа хранятся с точностью 3 знака
после десятичной точки
      10.125     m = 10125   k = 3 (фиксировано)                                   
                                     
      3.500   == 3500
 +    0.720   ==  720                               
--------------------                                     
      4.220   == 4220
      
      3.500 * 0.720 == 3500*720//1000 = 2520
      2.520                                    

      3.500 / 0.720 == 3500*1000//720 = 4861 
      4.861
      
Воспользовавшись этим классом, вычислить 100 знаков числа
e после десятичной точки (если не лень, то и 1000 знаков числа pi).

Примеры

Класс Polynom: "polynom.py"
Класс R2Vector: "R2Vector.py"
Модуль R2Graph: "R2Graph.py"

Лекция 7

Оконная графика в языке Python

Примеры оконных программ

Все примеры оконных программ используют модуль R2Graph, файл "R2Graph.py".

Рисование графика функции: "plotFunc.py"
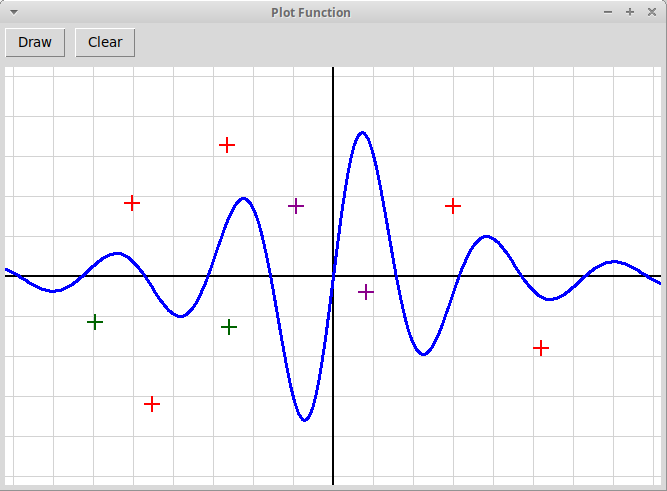
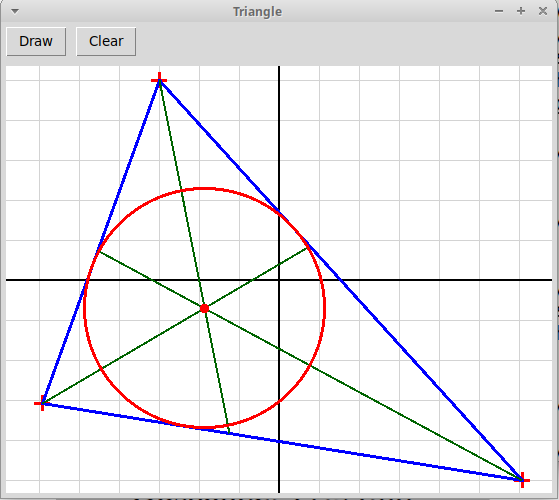
Нарисовать по трем кликам мыши треугольник, его биссектрисы и вписанную окружность: "triangle3.py" (вариант с возможностью захвата и перетаскивания мышью вершин треугольника с рисованием в реальном времени).
Цифровые часы: "digiclock.py"
Аналоговые часы: "analogclock.py"
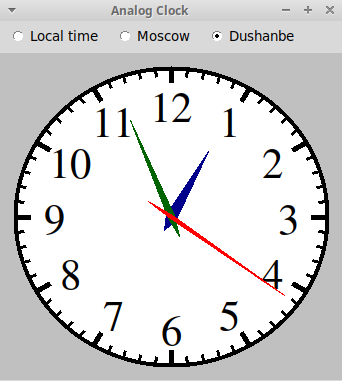
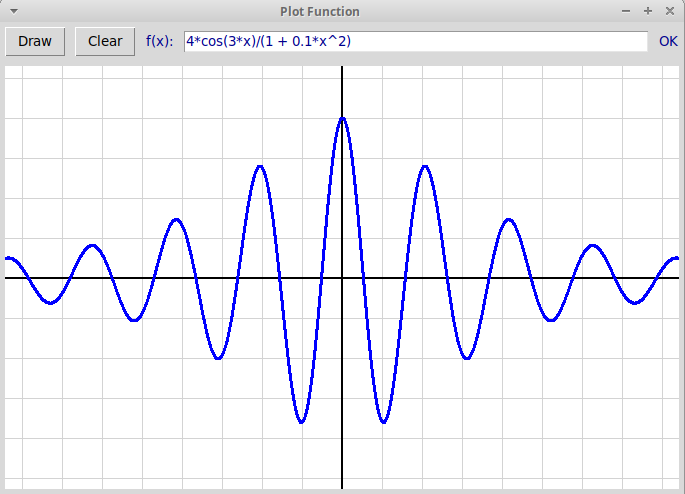
Парсер формул и рисование с его помощью графика функции, определение которой задается формулой в техтовом окне: "plotFunction.zip"

Архив проекта "plotFunction.zip" содержит 2 файла:

Задачи на тему "Оконное и графическое программирование в Python'е"

Решения задач обязательно должны использовать модуль tkinter, решения, использующие другие библиотеки классов, не принимаются! Желательно не писать программу с нуля, а использовать в качестве образца одну из программ, разобранных на лекциях; ссылки на файлы с программами приведены выше.

Всего имеется 7 вариантов задач. Студент должен сделать ту задачу, номер которой совпадает по модулю 7 с его номером по журналу.

Список задач

Нарисовать треугольник, окружность, описанную вокруг треугольника, и процесс ее построения (пересечение трех серединных перпендикуляров).
Нарисовать треугольник, точку Жергона и процесс ее построения. Точка Жергона — это точка пересечения трех отрезков (чевиан), соединяющих вершины треугольника с точками касания вписанной окружности:
Нарисовать треугольник и три его высоты. Каждая из высот треугольника проводится до точки пересечения с прямой, проходящей через две другие вершины треугольника.
Нарисовать треугольник, а также его медиану, биссектрису и высоту, проведенные из одной и той же вершины треугольника до пересечения с прямой, соединяющей две другие вершины. Медиана, биссектриса и высота рисуются разными цветами.
Пользователь отмечает кликами мыши n+1 точку на плоскости (x₀, y₀), (x₁, y₁), ..., (x_n, y_n), причем координаты x разных точек отличны друг от друга. Нарисовать график интерполяционного полинома степени n, постороенного по отмеченным узлам интерполяции: p(x): deg(p) = n, p(x_i) = y_i.
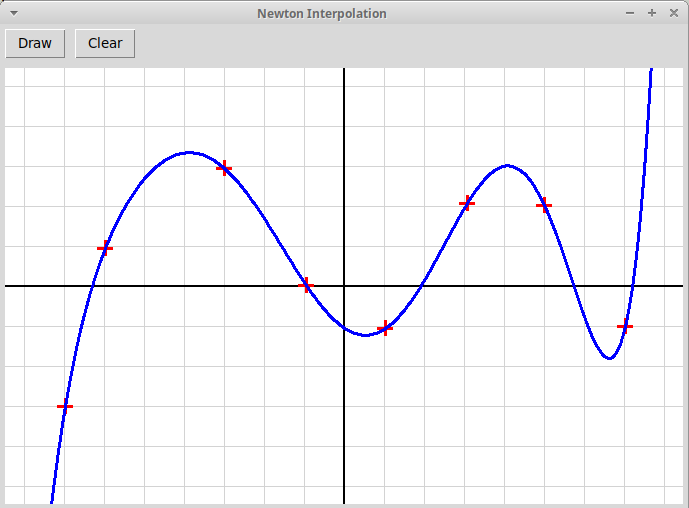
Следует использовать интерполяционную формулу Ньютона: p(x) = a₀ + a₁(x-x₀) + a₂(x-x₀)(x-x₁) + ... + a_n(x-x₀)(x-x₁)... (x-x_n-1) При добавлении еще одного узла интерполяции (x_n+1, y_n+1) коэффициенты a₀, ..., a_n остаются неизменными. К многочлену просто добавляется еще один член . . . + a_n+1(x-x₀)(x-x₁)... (x-x_n) Добавленный коэффициент вычисляется по формуле a_n+1 = (y_n+1 - p(x_n+1)) / ((x_n+1-x₀)(x_n+1-x₁)... (x_n+1-x_n))
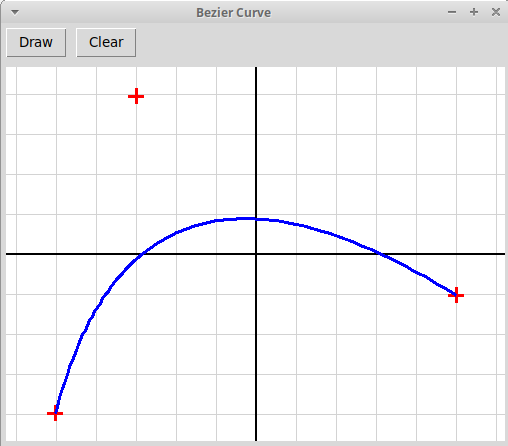
Нарисовать кривую Безье, построенную по узлам p₀, p₁, ..., p_n, отмеченным кликами мыши. Кривая Безье B{p₀, p₁, ..., p_n}(t) — это отображение вещественного отрезка [0, 1] в плоскость R², которое определяется рекуррентно (кривая порядка n определяется как линейная комбинация двух кривых порядка n-1): B{p₀}(t) = p₀
B{p₀, p₁}(t) = (1-t)·B{p₀}(t) + t·B{p₁}(t)
B{p₀, p₁, p₂}(t) = (1-t)·B{p₀, p₁}(t) + t·B{p₁, p₂}(t)
. . .
B{p₀,... , p_n}(t) = (1-t)·B{p₀,... p_n-1}(t) + t·B{p₁,..., p_n}(t)
На картинках изображены кривые Безье, построенные по трем узлам (квадратичная кривая) и четырем узлам (кубическая кривая):
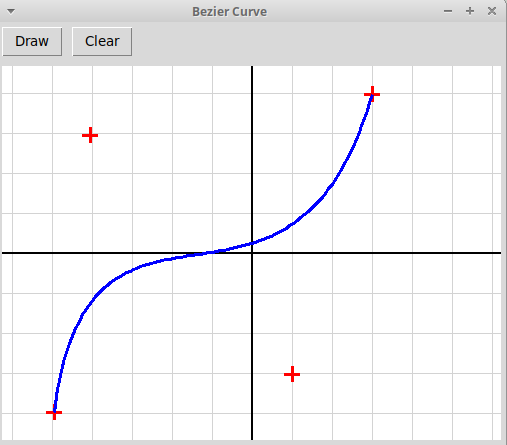
Переделать проект "plotFunction.zip", чтобы можно было рисовать сразу две функции в одном окне. Графики функций рисуются разными цветами. Тексты обеих функций задаются в двух текстовых полях (окнах типа tkinter.Entry):

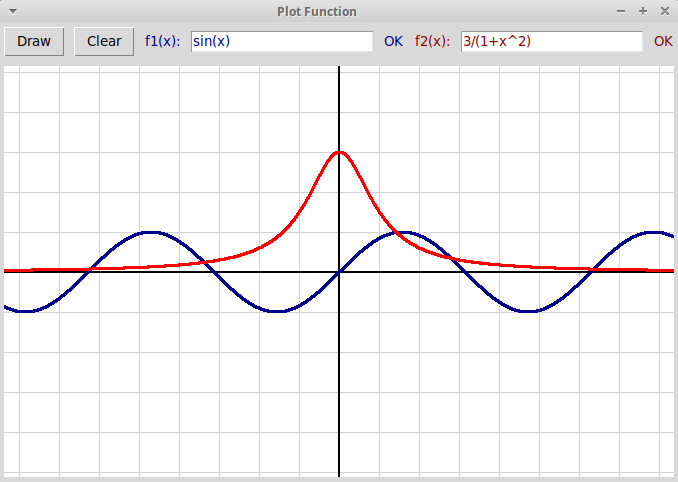
Указание. Следует создать два экземпляра объектов типа Parser: певый объект вычисляет первую функцию, второй — вторую функцию.
```
from tkinter import *
import math
from R2Graph import *
import lparser

parser1 = lparser.Parser()
function1Defined = False

parser2 = lparser.Parser()
function2Defined = False

def func1(x):
    if function1Defined:
        return parser1.evaluate(x = x)
    else:
        return 0.

def func2(x):
    if function2Defined:
        return parser2.evaluate(x = x)
    else:
        return 0.
```
Аналогично надо создать два текстовых поля, в которых задаются тексты двух функций, два поля для сообщений об ошибках компиляции и т.д.

Для языка Python разработано много разных модулей для программирования оконных приложений. В дистрибутиве языка Python для Windows представлен только один из них — это модуль tkinter. Он очень простой и удобный для программирования несложных приложений, что важно для начинающих программистов. Правда, можно отметить и его недостатки, которых лишены более продвинутые оконные библиотеки для Python'а — например, не реализовано сглаживание линий (antialiasing). Но мы будем использовать tkinter, поскольку только он представлен во всех дистрибутивах языка Python.

Для примера мы рассмотрим программу, которая по кликам мыши рисует треугольник и вписанную в него окружность: "triangle.py".

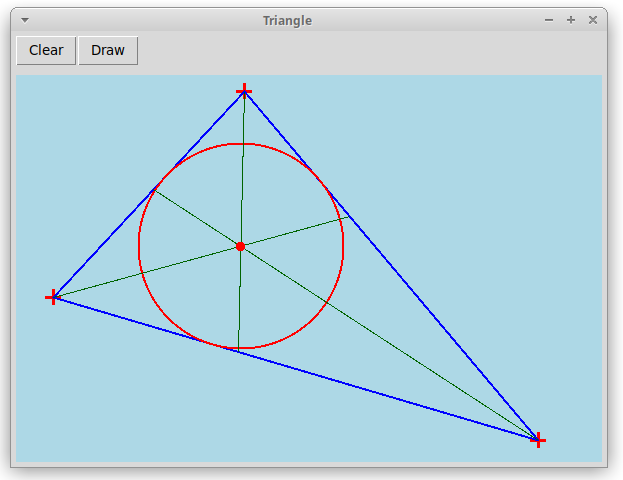
Программа начинается с импорта модуля tkinter (мы импортируем все описания из него). Также мы импортируем наши собственные классы R2Vector и R2Point, которые мы используем для решения разнообразных геометрических задач на плоскости R². Эти классы представлены в модуле R2Graph:

from tkinter import *
from R2Graph import *

Программу мы оформим в виде функции main, которая будет вызываться при исполнении скрипта. Все описания и другие функции будут локализованы внутри функции main:

from tkinter import *
from R2Graph import *

def main():
    rootWindow = Tk()
    rootWindow.title("Triangle")
    rootWindow.geometry("800x600")

    . . .

    rootWindow.mainloop()

if __name__ == "__main__":
    main()

Работа функции main начинается с создания корневого окна с заголовком "Triangle" и начальным размером 800 на 600 пикселей:

    rootWindow = Tk()
    rootWindow.title("Triangle")
    rootWindow.geometry("800x600")

В левой верхней части окна будут расположены две кнопки "Clear" и "Draw", а ниже будет располагаться дочернее окно, в котором происходит рисование и обработка кликов мыши. На приведенном выше рисунке окно рисования светло-голубого цвета.

Размещение дочерних окон — Layout Manager

Управление расположением дочерних окон в модуле tkinter может выполняться с помощью трех различных менеджеров расположения: place, pack, grid. Мы будем использовать менеждер pack, который в отличие от place позвляет корректировать расположение и размеры дочерних окон при изменении размеров окна верхнего уровня. Опуская фрагменты кода, укажем только тот код, который отвечает за создание и расположение дочерних окон. Их три: кнопки drawButton, clearButton и область рисования drawArea. Для горизонтальной группировки двух кнопок в верхней полоске окна мы создаем еще одно прозрачное окно panel типа Frame. Окно panel будет дочерним для окна верхнего уровня rootWindow, а кнопки drawButton и clearButton — дочерними для окна panel:

    panel = Frame(rootWindow)
    drawArea = Canvas(rootWindow, bg="lightBlue")
    . . .
    clearButton = Button(panel, text="Clear", command=clear)
    . . .
    drawButton = Button(panel, text="Draw", command=drawTriangle)
    . . .
    panel.pack(fill=X, padx=4, pady=4);
    clearButton.pack(side=LEFT)
    drawButton.pack(side=LEFT)
    drawArea.pack(fill=BOTH, side=TOP, expand=True, padx=4, pady=4)

Рассмотрим подробнее команды, создающие окна. Строка

    panel = Frame(rootWindow)

создает прозрачное окно типа Frame, которое нам нужно лишь для правильного размещения кнопок, которые потом будут добавляться внутрь окна panel как дочерние окна. Здесь единственный параметр конструктора — это окно, которое будет родительским для создаваемого окна, в нашем случае это rootWindow.

Команда

    clearButton = Button(panel, text="Clear", command=clear)

создает кнопку clearButton с надписью "Clear". Родительским окном для нее будет окно panel. Ключевой параметр command задает функцию, которая будет вызываться при нажатии на эту кнопку — это функция clear. Аналогично создается кнопка drawButton:

    drawButton = Button(panel, text="Draw", command=drawTriangle)

Отметим, что дочерние окна создаются невидимыми, они появятся на экране только после того, как будет выполнен метод pack.

. . .