| Глава 44. L-системы | ||
|---|---|---|
| | ||
Интересным применением черепашьей графики являются L-системы.
L-системой (точнее, её простейшей разновидностью, детерминированной контекстонезависимой L-системой) называют набор, состоящий из алфавита, аксиомы, и множества правил. Сейчас мы поясним все эти непонятные термины.
Алфавитом называется конечное множество, а его элементы — символами. Природа символов не важна, их единственная функция — отличаться друг от друга. Строкой над алфавитом назовём конечную последовательность символов алфавита. В наших задачах алфавит будет составлен из самых обычных символов, а строки над алфавитом будут самыми обычными строками.
Аксиома — это некоторая строка над алфавитом.
Каждое правило — это пара, состоящая из
предшественника
и последователя. Предшественник — это символ алфавита,
а последователь — строка над алфавитом. Вот пример пары:
AFBFA+HFA+FB-FA (стрелка
отделяет предшественника от последователя). В списке правил
символы-предшественники должны быть уникальными.
Приведём пример L-системы:
| алфавит | аксиома | правила | |||||
|---|---|---|---|---|---|---|---|
ABFHJ+-
| FB |
|
В дальнейшем, описывая L-системы, мы не будем указывать алфавит, поскольку он всегда будет состоять из символов, упомянутых в аксиоме и в правилах.
Как только L-система определена, она начинает развиваться в соответствии с её
правилами. Начальным состоянием L-системы является её аксиома. При дальнейшем
развитии эта строка, описывающая состояние, будет меняться. Развитие L-системы
происходит циклически. В каждом цикле развития строка просматривается от начала
к концу, символ за символом. Для каждого символа ищется правило, для которого
этот символ служит предшественником. Если такого правила не нашлось, символ
оставляется без изменений. Иными словами, для тех символов
X, для которых нет явного правила, действует неявное:
XX. Если же
соответствующее правило найдено, символ-предшественник заменяется на
строку-последователь из этого правила.
Для иллюстрации рассмотрим следующую L-систему (она называется Algæ — водоросль, поскольку её развитие моделирует рост одного из видов водорослей):
| аксиома | правила | ||
|---|---|---|---|
A |
|
В таблице приведены состояния этой L-системы, соответствующие первым десяти циклам развития системы.
| поколение | состояние |
|---|---|
| 0 | A |
| 1 | B |
| 2 | AB |
| 3 | BAB |
| 4 | ABBAB |
| 5 | BABABBAB |
| 6 | ABBABBABABBAB |
| 7 | BABABBABABBABBABABBAB |
| 8 | ABBABBABABBABBABABBABABBABBABABBAB |
| 9 | BABABBABABBABBABABBABABBABBABABBABBABABBABABBABBABABBAB |
Вряд ли кого-то удивит, что длины строк, кодирующих состояние такой L-системы,
образуют последовательность чисел Фибоначчи,
то есть такую числовую последовательность, в которой каждое число равняется
сумме двух предыдущих. Последовательностями Фибоначчи будут также количества
символов A и B в этих строках. Более
удивительным является тот факт, что в последовательности строк имеется та же
закономерность, что и в последовательности чисел Фибоначчи: каждая строка
является «суммой» (конкатенацией) двух предыдущих.
L-системы находят применение при моделировании процессов роста как живых организмов, так и неживых объектов (например, кристаллов, раковин моллюсков или пчелиных сот). Для моделирования требуется придать смысл символам алфавита L-системы.
Часто интерпретируют символы как программы на черепашьем языке, который знаком нам по главе 43. «Черепашья графика».
Например, если сопоставить в рассмотренной ранее L-системе Algæ
символам A и B программы
ROTATE 60 FORWARD 1
и
ROTATE -60 FORWARD 1
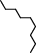
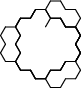
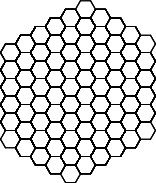
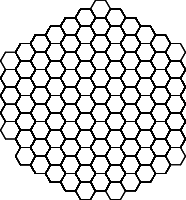
соответственно, черепаха, интерпретируя строки состояния для последовательных поколений L-системы, нарисует такие картинки:
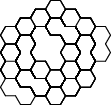
| поколения | изображения | ||
|---|---|---|---|
| 0, 5, 10 |
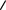 |
 |
 |
| 15, 20, 25 |
 |
 |
 |
Рассмотрим следующую последовательность ломаных:
Здесь показаны начальная ломаная (правильный треугольник) и первые пять этапов
преобразования ломаной. Внимательное их изучение позволяет выявить
закономерность, согласно которой происходят эти преобразования: каждый отрезок
заменяется на четырёхзвенную ломаную:
Если рисование единичного отрезка обозначить символом F,
а повороты на
против и по часовой стрелке кодировать соответственно символами
+ и -, то начальная ломаная (треугольник)
будет закодирована как F++F++F. Примем эту строку как
аксиому L-системы. Единственным правилом в такой L-системе будет замена
FF-F++F-F.
Итак, мы пришли к L-системе
| аксиома | правило |
|---|---|
F++F++F |
FF-F++F-F
|
Чтобы оставлять размер ломаных постоянным и компенсировать их трёхкратный рост
на каждом шаге, при рисовании ломаной -го поколения символу F
ставится в соответствие черепашья команда
FORWARD
Кривая, которая получится в результате бесконечного повторения такой процедуры, называется снежинкой Коха. Слова «результат бесконечного повторения процедуры» нуждаются в придании им точного математического смысла, но мы уклонимся от этого. Снежинка Коха даёт пример так называемых фрактальных кривых. Обсуждение фрактальных множеств состоится в разделе «Фракталы».
Другой пример использования L-систем — построение кривой Серпинского:
| аксиома | правила | интерпретация | ||||||
|---|---|---|---|---|---|---|---|---|
A |
|
|
Фрактальные множества, и, в частности, фрактальные кривые, замечательны тем, что их части в некотором смысле подобны целому множеству. Это их свойство называется самоподобием. Рассмотрение любого фрагмента фрактального множества под микроскопом при любом увеличении даёт картины, содержащие многочисленные копии (возможно, немного искажённые) исходного множества. Наиболее известное фрактальное множество — множество Мандельброта — показано на рисунке 44.1. «Множество Мандельброта» чёрным цветом вместе с его увеличенным фрагментом.
Это изображение получено с помощью программы XaoS,
которую мы очень рекомендуем установить (из пакета xaos, если у вас Linux) и попробовать в работе. Есть и другая
хорошая программа, Fractint,
которая так же позволяет изучать и рассматривать фрактальные множества, в том
числе построенные с помощью L-систем. Мы ещё вернёмся к этому изображению
в главе 48. «Множество Мандельброта».
Фрактальные множества — сравнительно недавно открытые объекты. Черты фрактальных множеств несут в себе многие природные объекты: растения, облака, горные вершины, дельты рек (см. рисунок 44.2. «Дельта реки Лена» с сайта http://ru.wikipedia.org), галактики. Да и сама вселенная в некотором смысле фрактальна.
Полюбоваться на изображения фрактальных множеств можно на сайте lenta.ru или в этом блоге.
Фракталы возникают и в математических моделях физических процессов. На рисунке 44.3. «Стохастическая паутина» показана фазовая картина стандартного отображения Чирикова — модели маятника с периодически колеблющейся точкой подвеса. Координаты чёрных точек имеют смысл угла отклонения маятника и его угловой скорости, взятые через промежутки времени, равные периоду колебаний подвеса. Координаты следующей точки получаются из координат предыдущей по очень простому правилу: При подходящем выборе начальной точки на плоскости последовательность точек, порождённая этим правилом, заполняет паутину с дырками (островами устойчивости). Каждый остров окружён несколькими островами поменьше, те в свою очередь тоже окружены островами, и так до бесконечности (конечно, самые мелкие острова, чей размер сравним с размером точек, мы не сможем увидеть на рисунке).
Несмотря на видимую сложность фрактальных множеств, способы их построения обычно очень просты. Судить об этом можно хотя бы по фрактальным множествам, построенным с помощью L-систем: достаточно начального состояния и набора правил, описывающих эволюцию L-системы, чтобы построить последовательность множеств, приближающихся к фрактальному с любой степенью точности. Всё обилие информации, описывающей фрактальное множество, можно вывести из сравнительно небольшого объёма информации, заключённой в аксиоме и правилах. Это наблюдение позволяет применять фракталы для очень эффективного сжатия изображений (имеется в виду не геометрическое сжатие, а существенное сокращение объёма информации, требуемой для описания изображения без заметной потери качества). Изображение разбивается на квадраты, и для каждого из них подбирается набор начальных условий и правил для построения фрактала, наиболее похожего на изображение в фрагменте. Объём информации, заключённой в таком описании фрактала, обычно намного меньше, чем в точечном описании картинки в фрагменте.
Наблюдения за высшими растениями приводят нас к выводу, что тело растения представляет собой ствол с отростками (это могут быть ветви дерева, листья, цветки). На отростках в свою очередь возможны другие отростки.
Применим это наблюдение для компьютерного моделирования дерева, для чего попытаемся выделить главное свойство всех деревьев, независимо от породы. А свойство это заключается в следующем: дерево представляет собой или голый ствол, или ствол с растущими из него несколькими ветками. Каждая ветка устроена согласно тому же самому принципу: она является деревом.
Такое свойство дерева можно было бы взять в качестве основы для модели, однако оно допускает деревья с бесконечным количеством веток (чего в природе не встречается). Глубина дерева (то есть максимальная длина последовательности «ствол, первичная ветка, вторичная ветка, третичная ветка, …, самая последняя ветка») должна быть конечной.
Поэтому определим дерево глубины (дерево -ого порядка). Деревом -ого порядка будем называть ствол с растущими на нём ветками, которые является деревьями -го порядка. Чтобы такое определение не привело к деревьям с отрицательной глубиной, скажем, что дерево нулевого порядка — это голый ствол.
Дерево неудобно рисовать одним росчерком карандаша. Оно является не ломаной, а, скорее, набором отрезков. Черепаха позволяет рисовать наборы отрезков, не связанные в ломаную, и для такого рисования имеется два средства. Во-первых, это возможность поднимать и опускать карандаш и сдвигаться вперёд с поднятым карандашом. Во-вторых, это возможность запоминать и восстанавливать состояние. Мы попробуем второй способ.
Дерево в нулевом поколении представляет собой единственную почку. В следующем, первом поколении из почки вырастает нижняя половинка побега, затем почка для будущей ветки, наклонённой влево на , затем верхняя половинка побега с двумя почками, наклонёнными влево и вправо на те же . В следующих поколениях старые половинки побега удлиняются в два раза, а с почками происходят те же самые метаморфозы, что и при переходе от нулевого к первому поколению. На следующей иллюстрации изображены три первых поколения дерева:
| поколения | изображение | ||
|---|---|---|---|
| 0, 1, 2 |
 |
 |
 |
Здесь почки показаны как короткие красные отрезки только для пояснения, в итоговом изображении они не появятся. Чтобы компенсировать рост размеров изображения, длины отрезков на каждом шаге сокращаются вдвое.
Если переложить всё сказанное на язык L-систем, получим следующее описание:
| аксиома | правила | интерпретация | |||||||
|---|---|---|---|---|---|---|---|---|---|
X |
|
|
Здесь требуется пояснение. Символы X и F
обозначают соответственно почку и половинку побега. Хотя почки невидимы (для
символа X отсутствует интерпретация), они отмечают место для
будущих побегов. Предшествующие им символы +
и - показывают, что всё, что из них вырастет, будет
повёрнуто. Фразы [+X] и [-X] в правиле
XF[+X]F[-X]+X означают,
что после рисования побега, выросшего на месте почки, состояние черепахи будет
восстановлено. Правило FFF отвечает за удвоение
длины побега.
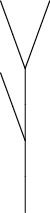
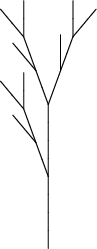
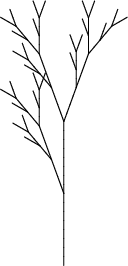
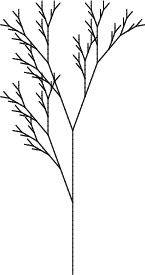
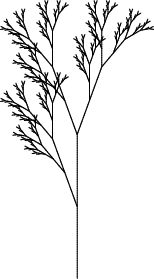
Приводим изображения первых восьми поколений дерева, полученные такой L-системой:
| поколения | изображение | |||
|---|---|---|---|---|
| 0, 1, 2, 3 |
 |
 |
 | |
| 4, 5, 6, 7 |
 |
 |
 |
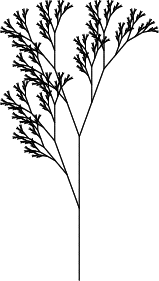 |
Получившееся дерево изящно, но оно слишком правильное, и, следовательно, неправдоподобное. Кроме того, в этом дереве не отражена важная черта реальных деревьев: ствол толще ветвей, растущих из него, и темнее этих ветвей.
Теперь разберём пример построения более реалистичного дерева с помощью
L-системы. Отрезки, образующие дерево, разделим на два типа. Отрезок типа
X — это ветвь, на которой в следующем поколении вырастут две
ветви потоньше, покороче и светлее, и, кроме того, наклонённые вправо и влево
на случайный угол, равномерно распределённый в пределах от
до
.
Отрезок типа F — это ветвь, от которой уже ответвились две
ветви. Ветви типа X назовём
терминальными
(конечными), а ветви типа F —
нетерминальными.
Дерево в нулевом поколении представляет собой одну терминальную ветвь.
Для построения нужной L-системы нам понадобятся символы X
и F (для ветвей обоих типов), +
и - (для поворота черепахи соответственно влево и вправо на
случайный угол), @ (для осветления текущего цвета рисования,
уменьшения толщины и длины штрихов), и, конечно, скобки [
и ] (для запоминания и последующего восстановления
запомненных состояний черепахи — её положения и направления, а также цвета,
толщины и длины штриха).
Теперь займёмся правилом L-системы. В каждом цикле развития дерева каждая
терминальная ветвь превращается в нетерминальную, от которой что-то
ответвилось: XF[…]. Эту ответвившуюся
растительность мы заключаем в скобки, в которые первым делом помещает символ
@, ответственный за осветление, утоньшение и укорачивание
ветвей. Затем рисуем правую ветвь: [-X]. Скобки здесь нужны
для того, чтобы запомнить положение и направление черепахи; ведь предстоит
поворот на случайный угол. Рисуем левую ветвь:
+X.
Итак, мы приходим к следующему описанию L-системы:
| аксиома | правило | интерпретация | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
X |
|
|
Несколько последующих циклов развития дерева приведены на рисунке:
| поколения | изображение |
|---|---|
| 0 |
 |
| 1 |
 |
| 2 |
 |
| 3 |
 |
| 4 |
 |
| 5 |
 |
| 6 |
 |
| 7 |
 |
| 8 |
 |
| 9 |
 |
| 10 |
 |
| 11 |
 |
| 12 |
 |
| 13 |
 |
Другой, рекурсивный подход к построению такого дерева описан в нашем пособии METAPOST. Краткий курс в разделе «Макрокоманды».
Возможны различные обобщения контекстонезависимых детерминированных L-систем. Они дают более сложные модели роста.
Стохастические (или недетерминированные) L-системы содержат элемент случайности в своём развитии. Они допускают по нескольку правил для каждого символа-предшественника. Одно из нескольких правил для данного символа строки состояния каждый раз выбирается случайно, с некоторой заданной вероятностью. Само собой, каждому из правил для данного предшественника приписывается вероятность выбора правила — число от нуля до единицы (сумма таких чисел должна равняться единице).
Наш пример с деревом, хотя и содержит что-то случайное, не является стохастической L-системой. Само развитие системы полностью детерминировано, то есть вполне определяется аксиомой и правилами. Всяческая случайность дана на откуп рисующей черепахе.
Другой путь к обобщению L-систем тоже подразумевает множественные правила для одного предшественника. Только теперь выбор одного правила из многих не случаен, а обусловлен контекстом — символами, расположенными по соседству с тем, к которому применяется правило. Чем большее число соседних символов создают контекст, тем сложнее получится система.
Можно в качестве состояния L-системы брать вместо строки более сложную сеть, составленную из символов. Каждый символ в сети связан с одним или несколькими другими отношением соседства. Например, сеть может представлять собой прямоугольную таблицу. С этой точки зрения модель, рассмотренная в главе 37. ««Жизнь» Джона Конвея», даёт пример детерминированной контекстозависимой L-системы на прямоугольной таблице символов. Алфавит состоит из двух символов: один означает мёртвую клетку, а другой — живую. Контекст состоит из восьми символов, окружающих данный. Для обоих предшественников задаётся по правил — именно столько состояний может принимать контекст.
Имеется целая отрасль в компьютерной науке, посвящённая алгоритмическому моделированию растений — алгоритмическая ботаника.
Вопросам алгоритмической ботаники посвящён прекрасный сайт «Algorithmic Botany at the University of Calgary». Там имеется большой раздел с публикациями. Обращаем особое внимание на книгу «The Algorithmic Beauty of Plants» (P. Prusinkiewicz, A. Lindenmayer).