Программирование

Материалы для 1-го курса мехмата

2-й семестр: список задач

Задачи даются по темам. Номера задач для каждого студента определяются следующим образом. Пусть N — номер студента по журналу, и пусть в теме даны k задач. Тогда студенту нужно сделать задачу с номером r, где r == N (mod k), т.е. выбрать ту задачу, номер которой при делении на k дает тот же остаток, что и номер студента. Например, если в теме 4 задачи, а номер студента равен 10, то нужно сделать задачу 2; если номер студента 16, то нужно сделать задачу 4.

1. Автоматический тестер по теме "Матрицы"

Для получения условия задачи с номером N надо выполнить команду

    tasktest matrix2 N -text

(например, для задачи 101 команда "tasktest matrix2 101 -text"), текст задания будет записан в файл "TheTask.txt". Для прохождения теста надо выполнить команду

    tasktest matrix2 N file.cpp

где file.cpp — имя файла с программой.

Пример теста по матрицам "matrix2"

Подробое описание конкретного теста, пример программы для его прохождения и особенности ее написания см. здесь.

2. Матрицы и метод Гаусса

В всех задачах следует использовать метод Гаусса приведения матрицы к ступенчатому виду. В качестве образца дается файл, где реализован метод Гаусса в виде функции с прототипом

    int gauss(double *a, int rows, int cols, double eps = 1e-8);

которая приводит матрицу к ступенчатому виду и возвращает ранг матрицы, т.е. число ненулевых строк в ее ступенчатом виде. В качестве теста матрица считывается из файла "input.txt", затем она приводится к ступенчатому виду, печатается ее ранг и в случае квадратной матрицы — оределитель; ступенчатая матрица записывается в файл "output.txt". Вот исходный код программы, скачать файл можно по ссылке "gauss.cpp".

Дано m векторов линейного пространства размерности n. Требуется найти среди них максимальную линейно независимую систему (базис линейной оболочки) и вывести ее в файл. Исходные данные записаны в файле "input.txt" в следующем формате: сначала целые числа m и n, затем m векторов, каждый из которых задан n вещественными числами. Числа в файле разделяются пробелами или переводами строк. Результат работы программы надо записать в том же формате в файл "output.txt" (сначала целые числа k и n, где k — число элементов в максимальном линейно независимом подмножестве исходного множества векторов, затем сами вектора этого подмножества).
Для квадратной невырожденной матрицы вычислить обратную матрицу. Исходная матрица читается из файла "input.txt", обратную матрицу нужно записать в файл "output.txt". Формат представления матриц такой же, как и в задаче 1.
Решить систему линейных уравнений с невырожденной квадратной матрицей. В файле "input.txt" записана расширенная матрица системы, содержащая n строк и n+1 столбец, последний столбец содержит свободные члены уравнений:
a_i1 x₁ + a_i2 x₂ + ... + a_in x_n = b_i, i = 1, 2, ..., n.
Ответ (набор чисел x₁, x₂, ... x_n) надо записать в файл "output.txt".
Дана однородная линейная система уравнений (свободные члены уравнений равны нулю) с вырожденной квадратной матрицей A:
A X = 0
(здесь X — столбец неизвестных x₁, x₂, ... x_n). Найти какое-нибудь ненулевое решение системы.
Исходную матрицу прочесть из файла "input.txt" (формат такой же, как и в задаче 1), ответ записать в файл "output.txt".

3. Вычисление элементарных функций, представленных степенными рядами

Во всех задачах требуется не просто просуммировать ряд, представляющий элементарную функцию. Как правило, подобный ряд можно эффективно вычислять не для всех значений из области определения функции (он может не сходиться либо сходиться очень медленно, либо ошибка накапливается очень быстро). Поэтому требуется воспользоваться некоторым тождеством (например, периодичностью функции sin(x)), с помощью которого можно свести вычисление функции к суммированию ряда для "удобных" значений переменной x.

Вычислить arctg(x).
Вычислить arcsin(x).
Вычислить arccos(x).
Вычислить ln(x).
Вычислить x^α

Подробное описание этих задач.

4. Сортировка

Лекция Алгоритмы сортировки (презентация)

Задачи по теме "Сортировка"

Нужно решить одну задачу, номер которой совпадает по модулю 3 с номером студента в журнале. В качестве примера можно использовать файл tstSort0.cpp, содержащий функции генерации случайных массивов и их печати, а также прототипы функций сортировки разными методами (реализация дана только для функций bubbleSort и insertionSort, реализации остальных оставлены в качестве задач).

Написать функцию сортировки массива методом пирамиды HeapSort. Прототип функции:
```
void heapSort(
    double *a,  // Pointer to the beginning of array
    int n       // Size of array
);
```
Написать функцию сортировки массива методом слияния MergeSort, используя нисходящую (рекурсивную) схему реализации. Прототип функции:
```
void mergeSortRecursive(
    double *a,          // Beginning of array
    int n,              // Size of array
    double* tmpMemory = nullptr // Temporary memory to use
);
```
Написать функцию сортировки массива методом слияния MergeSort, используя восходящую (итеративную) схему реализации. Прототип функции:
```
void mergeSortBottomTop(
    double *a,          // Beginning of array
    int n,              // Size of array
    double* tmpMemory = nullptr // Temporary memory to use
);
```

5. Вычисление определенных интегралов

Описание квадратурных формул.

Задачи можно выполнять в одном из двух вариантов:

простой вариант — вычислить приближенное значение интеграла по отрезку [a, b] для заданного числа N разбиений отрезка (число N определяется по заданной точности ε);
более сложный (но и более интересный) вариант — применить алгоритм автоматического определения величины отрезка h разбиения, при котором h на каждом следующем шаге алгоритма уменьшается в 2 раза. Алгоритм заканчивается, когда два последовательно вычисленных значения квадратурной формулы отличаются не более чем на ε.

Вычислить значение интеграла от некоторой функции y=f(x) по отрезку [a, b], используя формулу трапеций.
Вычислить значение интеграла от некоторой функции y=f(x) по отрезку [a, b], используя формулу Симпсона.

6. Геометрия и оконная графика

При решении геометрических задач следует использовать классы R2Vector и R2Point, которые представляют вектор и точку на 2-мерной плоскости R². Определения этих типов (т.е. классы языка C++) даны в файле "R2Graph.h", который надо переписать в текущую директорию и подсоединять с помощью директивы

#include "R2Graph.h"

Также надо переписать в текущую директорию файл "R2Graph.cpp", содержащий реализацию некоторых методов и глобальных функцию, использующих классы R2Vector и R2Point (например, найти пересечение двух прямых, каждая прямая задается точкой и направляющим вектором). При компиляции проекта надо подключить также этот файл, например:

    g++ -o myTask myTask.cpp R2Graph.cpp

Пример консольного приложения, вычисляющего окружность, вписанную в теругольник (вычисляются ее центр и радиус). Вершины треугольника вводятся с клавиатуры, результат выводится в выходной поток: "inCircle.cpp".

6.1. Геометрические задачи, не требующие рисования в окне

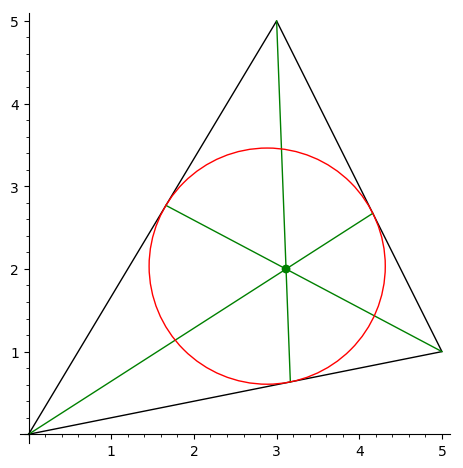
Вычислить точку Жергона треугольника.
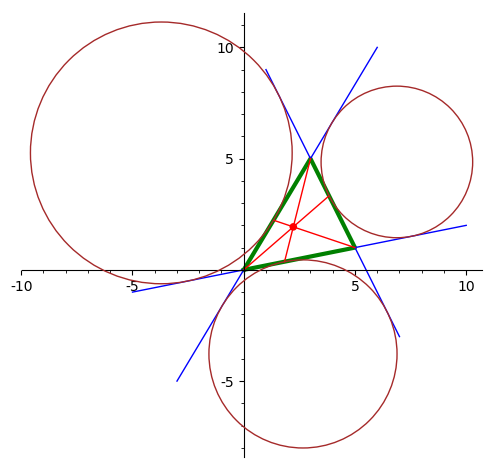
Вычислить точку Нагеля теругольника как пересечение чевиан, проведенных к точкам касания внешневписанных окружностей.
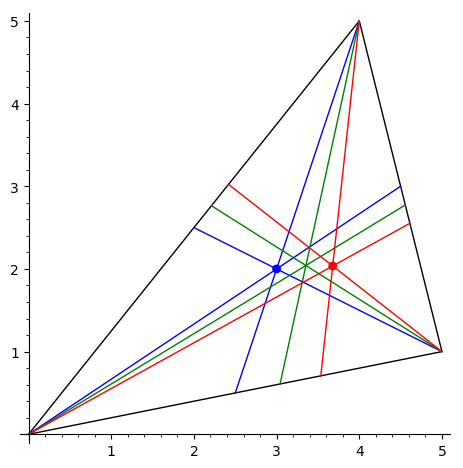
Вычислить точку Лемуана треугольника, которая построена как точка, изогонально сопряженная к точке пересечения медиан.
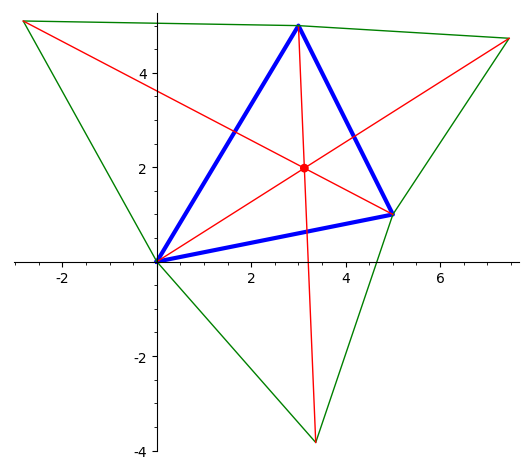
Вычислить точку Ферма-Торичелли треугольника (точка, минимизирующая сумму расстояний до вершин треугольника).Вот процесс ее построения:

6.2. Геометрические задачи с графической иллюстрацией

Для оконной графики мы используем библиотеку классов Qt и среду для разработки Qt-проектов "qtcreator". К достоинствам Qt относится то, что исходный код Qt-проекта не зависит от операционной системы (если не использовать специфические функции различных ОС и оставаться только в рамках Qt, то исходный код одинаковый для Unix, MS-Windows, MAC OS-X и т.д.). Кроме того, программировать на Qt очень удобно, в Qt предусмотрено огромное множество функций, классов и других инструментов для создания самых разнообразных программ.

Недостаток Qt в том, что необходимо изучить эту систему разработки в дополнение к изучению языков C и C++. Впрочем, библиотека Qt очень естественна и, наверно, по сравнению с другими средами разработки оконых приложений наиболее проста (насколько вообще может быть проста система разработки графических оконных приложений).

6.2.1. Минимальные сведения об оконных графических системах и оконных приложениях

Любая оконная программа занимается обработкой сообщений об оконных событиях. В центре программы — цикл обработки событий:

    цикл до бесконечности выполнять
    | получить сообщение о событии(вых: event)
    | обработать событие(вход: event)
    конец цикла

Таким образом, классическая оконная программа большую часть времени ничего не делает, ожидая, когда произойдет событие. Когда происходит событие, операционная система добавляет сообщение о нем в очередь; программа обрабатывает события (т.е. совершает действия, логически связанные с событием) в порядке их поступления в очередь. Отметим, что цикл обработки событий может быть спрятан внутри стандартных функций или методов и явно не присутствать в программе (так, в Qt он стартует при вызове метода QApplication::exec()).

В различных операционных системах набор оконных событий может различаться, начиная от небольшого количества событий (около 15) в первых версиях Mac OS и заканчивая чрезвычайно детализированным их набором в Win32. Для программирования несложных оконных приложений на Qt достаточно обрабатывать следующие события (укажем также методы, которые обрабатывают эти события — это методы класса QWidget, который в Qt представляет базовое окно).

Перерисовка окна: void paintEvent(QPaintEvent *event);
Нажатие на клавишу мыши: void mousePressEvent(QMouseEvent* event);
Отпускание клавиши мыши: void mouseReleaseEvent(QMouseEvent* event);
Перемещение курсора мыши: void mouseMoveEvent(QMouseEvent* event);
Изменение размера окна: void resizeEvent(QResizeEvent *event);

(В этот список не включены события, связанные с клавиатурой.)

Технология обработки этих событий при программировании на Qt/C++ состоит в перекрытии (т.е. переопределении) указанных методов для класса, реализующего в Qt-программе окно, в котором выполняется рисование и работа с различными графическими объектами с помощью мыши. Окно,в котором происходит рисование, наследуется из базового типа QWidget (базовое окно в Qt).

Однако, помимо событий "базового" уровня (перерисовка окна, нажатие или отпускание клавиш мыши, ее движение), можно рассматривать и более сложные события, которые являются комбинациями базовых — например, mouse click (щелчок мыши), double click и т.п. Рассмотрим, например, окно типа QPushButton, представляющее кнопку. Комбинация базовых событий нажатия и отпускания клавиши мыши, когда курсор находится в этом окне, составляет сложное событие "clicked". В Qt для обработки таких "составных" событий используется механизм сигналов и слотов. Считается, что при наступлении такого сложного события окно (в нашем примере кнопка) посылает сигнал о событии (в тексте Qt-программы сигнал посылается с помощью ключевого слова emit). Этот сигнал может обрабатываться другими объектами, методы, обрабатывающие сигналы, называются слотами (slot). Связь между сигналами и обрабатывающими их слотами в Qt устанавливается с помощью метода QObject::connect. Например, следующий фрагмент программы

    QObject::connect(
        &clearButton, SIGNAL(clicked()),        
        &window, SLOT(clear())    
    );

устанавливает связь между сигналом clicked() кнопки clearButton и слотом clear() объекта window, который обрабатывает нажатие на эту кнопку.

(Ключевые слова signal, emit, slot не являются частью языка С++, это небольшое расширение языка С++, которое используется в Qt. При сборке проекта исходный текст программы сначала обрабатывается утилитой moc (Meta Object Compiler), в результате которого создается уже программа на чистом C++, которая реализует связь между сигналами и слотами при помощи объектов типа QMetaObject. Утилиту moc можно рассматривать как препроцессор исходного кода на языке С++, расширенном конструкциями Qt. Для практического программирования не обязательно рассматривать C++ код после препроцессирования или даже понимать принципы его реализации.)

6.2.2. Учебный проект на Qt: рисование графика функции и ввод массива точек

Рассмотрим проект, который можно использовать как шаблон для написания простых графических Qt-программ: "PlotFunc.tgz". Для распаковки его в Unix'е сохраните этот файл в текущей директории и выполните команду

    tar xzvf PlotFunc.tgz

Будет создан каталог "PlotFunc" с исходными файлами проекта. Нужно перейти в него и запустить qtcreator:

    cd PlotFunc
    qtcreator PlotFunc.pro &

(последняя команда запускает систему разработки qtcreator для проекта "PlotFunc.pro"; в Qt файлы с расширением .pro используются для описания проектов).

Вот как выглядит работающая программа:

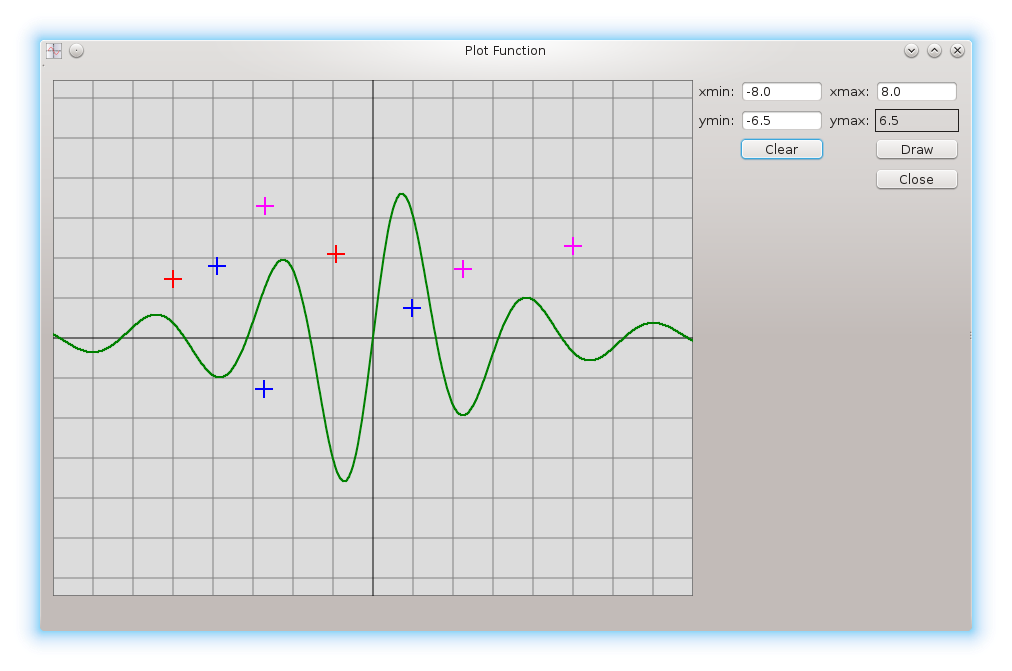
Программа рисует график функции, заданной непосредственно в коде программы:

    double f(double x) {
        return 4.*sin(2.*x)/(1. + 0.2*x*x);
    }

Помимо графика функции, рисуются оси координат и координатная сетка ("клетчатая бумага"). Пользователь может отмечать кликами мыши точки, в ответ программа рисует крестики в отмеченных точках; цвет крестиков соответствует клавишам мыши (левая клавиша — синий крестик, правая — красный, средняя — малиновый).

Все крестики можно стереть, нажав на кнопку Clear в окне. Можно также изменять масштаб изображения и положение начала координат, редактируя значения в текстовых полях xmin, xmax, ymin (значение ymax определяется автоматически так, чтобы масштабы по осям X и Y были одинаковы). После изменения значений следует нажать кнопку Draw для перерисовки окна. По нажатию кнопки Close программа завершает работу.

6.2.3. Устройство проекта PlotFunc

Проект состоит из следующих файлов:

PlotFunc.pro: Файл описания проекта.
main.cpp: Запускающая функция (стартер).
mainwindow.h, mainwindow.cpp: Окно вернего уровня (форма), содержащее кнопки, текстовые поля и дочернее окно для рисования. h-файл содерит описание класса MainWindow, cpp-файл содержит реализацию методов класса.
mainwindow.ui: Описание оконной формы в виде XML-файла (редактируется в оболочке qtcreator с помощью программы qtdesigner; используется для автоматической генерации С++ кода, создающего эту форму при работе программы).
drawarea.h, drawarea.cpp: Дочернее окно, в котором выполняется рисование и ввод точек кликами мыши. h-файл содерит описание класса DrawArea, cpp-файл содержит реализацию методов класса.
R2Graph.h, R2Graph.cpp: Файлы, содержащие описание и реализацию классов для поддерки двумерной графики, в частности, классов R2Vector и R2Point, представляющих вектор и точку с вещественными координатами на двумерной плоскости R².

Отметим, что для решения любых задач из приведенного ниже списка достаточно вносить изменения только в файлы drawarea.h и drawarea.cpp, другие файлы трогать не нужно!

6.2.4. Класс DrawArea

Класс DrawArea представляет собой дочернее окно, в котором происходит рисование и ввод точек кликами мыши. Оно является частью окна вернего уровня и меняет свой размер синхронно с изменением размера родительского окна. Рисование в окне выполняется в методе paintEvent, который вызывается при получении сообщения о событии типа QPaintEvent (перерисовка окна). Вот реализация этого метода:

void DrawArea::paintEvent(QPaintEvent* event) {
    QPainter painter(this);
    painter.fillRect(0, 0, width(), height(), bgColor);

    drawCoordSystem(&painter);
    painter.setRenderHint(QPainter::Antialiasing); // Smoothing
    plotFunction(&painter, &f);
    drawPoints(&painter);

    event->accept();
}

Комментарии к тексту. Отметим, что любое рисование в окне совершается с помощью объекта типа QPainter (рисователь, художник), иногда в оконных системах подобные объекты называют "графическим контекстом" или "контекстом устройства" (device context). Так что перед рисованием сначала создается объект painter, указатель на который затем передается во все функции и методы, выполняющие рисование.

    QPainter painter(this);

Параметр this в скобках означает указатель на текущее окно. Отметим, что рисователь можно создавать не только для окна, но и для объекта типа QImage, который в Qt используется для работы с изображениями в памяти компьютера. В последнем случае рисование выполняется внутри изображения (т.е. непосредственно не отображается в окне); изображение потом можно отобразить в окне или, например, записать в файл в любом из популярных графических форматов.

Следующая строка очищают прямоугольник окна (заполняют его цветом фона bgColor, bg от слова background; переменная bgColor инициализирутся светло-серым цветом Qt::lightGray в конструкторе класса DrawArea):

    painter.fillRect(0, 0, width(), height(), bgColor);

И, наконец, программа рисует сначала систему координат с координатной сеткой ("бумага в клеточку"), затем график функции и множество точек, отмеченных мышкой:

    drawCoordSystem(&painter);

    painter.setRenderHint(QPainter::Antialiasing); // Smoothing
    plotFunction(&painter, &f);
    drawPoints(&painter);

Эти три действия оформлены в виде трех отдельных методов. Во все методы передается указатель на объект painter, с помощью которого выполняется рисование. Перед рисованием графика функции устанавливается режим сглаживания линий (Antialiasing):

    painter.setRenderHint(QPainter::Antialiasing); // Smoothing

Разберем для примера метод plotFunction, рисующий график функции y=f(x).

void DrawArea::plotFunction(
    QPainter* painter, double (*f)(double)
) {
    QPen greenPen(Qt::darkGreen);
    greenPen.setWidth(2);
    painter->setPen(greenPen);
    painter->setBrush(Qt::NoBrush);

    QPainterPath path;

    // double dx = 0.01;
    // Compute dx that corresponds to 1 pixel
    R2Point h0, h1;
    h0 = mapFromPixels(QPointF(0., 0.));
    h1 = mapFromPixels(QPointF(1., 0.));
    double dx = h1.x - h0.x;

    R2Point p(xmin, (*f)(xmin));
    path.moveTo(mapToPixels(p));
    while (p.x < xmax) {
        p.x += dx;
        p.y = (*f)(p.x);
        path.lineTo(mapToPixels(p));
    }
    painter->drawPath(path);
}

В начале метода создается темно-зеленое перо (объект типа QPen) толщиной 2 пикселя и устанавливается как текущее перо рисователя:

    QPen greenPen(Qt::darkGreen);
    greenPen.setWidth(2);
    painter->setPen(greenPen);

Затем определяется шаг dx по оси абсцисс, который соответствует ширине одного пикселя экрана:

    // Compute dx that corresponds to 1 pixel
    R2Point h0, h1;
    h0 = mapFromPixels(QPointF(0., 0.));
    h1 = mapFromPixels(QPointF(1., 0.));
    double dx = h1.x - h0.x;

Наиболее важная часть этого метода — рисование ломаной, аппроксимирующей кривую графика функции:

    QPainterPath path;
    . . .

    R2Point p(xmin, (*f)(xmin));
    path.moveTo(mapToPixels(p));
    while (p.x < xmax) {
        p.x += dx;
        p.y = (*f)(p.x);
        path.lineTo(mapToPixels(p));
    }
    painter->drawPath(path);

Для этого используется объект path типа QPainterPath, с помощью которого строится ломаная, состоящая из последовательности точек. Вначале устанавливается начальная точка пути:

    R2Point p(xmin, (*f)(xmin));
    path.moveTo(mapToPixels(p));

Затем в цикле последовательно добавляются точки на графике функции:

    while (p.x < xmax) {
        p.x += dx;
        p.y = (*f)(p.x);
        path.lineTo(mapToPixels(p));
    }

Эти точки можно потом использовать для рисования пути через эти точки (это может быть как просто ломаная, так и сглаженная кривая, построенная как сплайн) или многоугольника с данными вершинами (его внутренность может быть закрашена). В данном случае мы просто рисуем ломаную, не закрашивая внутренность многоугольника, для этого ранее устанавливается "фиктивная" кисть:

    painter->setBrush(Qt::NoBrush);
    . . .
    painter->drawPath(path);

6.2.5. Две системы координат в окне: математическая и пиксельная

В Qt по умолчанию используется пиксельная система координат в окне. В ней ось Y направлена вниз, а начало координат находится в левом верхнем углу окна. Единица в пиксельной системе координат соответствует размеру одного пикселя. Чтобы нарисовать линию, мы указываем две точки с пиксельными координатами — объекты типа QPointF, который в Qt представляет точки с вещественными координатами. Например, данный фрагмент кода

    painter->drawLine(
        QPointF(20., 50.), QPointF(200., 150.)
    );

рисует отрезок с координатами концов (20., 50.) и (200., 150.) в пиксельной системе координат:

Пиксельная система координат не очень удобна для рисования математических объектов, поэтому мы все вычисления проводим в математической системе координат. Она использует вещественные числа вместо целых для представления координат точек и векторов. При рисовании объектов ось Y направлена вверх, как это принято в математике, а начало координат может находиться в произвольной точке окна. Также можно выбрать и произвольный масштаб, он никак не связан с размером пикселя или разрешением окна. В нашем проекте мы задаем минимальное и максимальное значения координаты x от -8.0 до 8.0, начало координат находится в центре окна, минимальное и максимальное значения координаты y вычисляются, исходя из геометрии реального окна так, чтобы масштабы по осям были одинаковы.

Для работы с точками и векторами на плоскости в математической системе координат мы используем классы R2Point и R2Vector, которые определены и реализованы в файлах "R2Graph.h" и "R2Graph.cpp". Основная идея в том, чтобы все определения геометрических объектов, операции с ними, вычисления и т.п. производить в терминах математических точек и векторов, и лишь в самый последний момент перед рисованием отображать точки в математической системе координат на точки в пиксельных координатах. Для этого в классе DrawArea имеется метод mapToPixels:

    class DrawArea: public QWidget {
        . . .
        QPointF mapToPixels(const R2Point& p) const;
        . . .
    };

С его помощью для точки p с математическими координатами можно получить ее пиксельные координаты, т.е. объект q типа QPointF:

    R2Point p;
    . . .
    QPointF q = mapToPixels(p);

Пиксельные координаты можно получать непосредственно перед рисованием, например, при вызове метода DrawLine. Так, фрагмент кода

    R2Point p0(0.5, 2.3);
    R2Point p0(3.75, -1.5);
    painter->drawLine(
        mapToPixels(p0), mapToPixels(p1)
    );

рисует отрезок с концами в точках с математическими координатами (0.5, 2.3) и (3.75, -1.5):

Наряду с методом mapToPixels, который отображает точку с математическими координатами на соответствующую точку с пиксельными координатами, в классе DrawArea реализовано также и обратное отображение mapFromPixels:

    class DrawArea: public QWidget {
        . . .
        QPointF mapToPixels(const R2Point& p) const;
        R2Point mapFromPixels(const QPointF& q) const;
        . . .
    };

С его помощью по точке точке q с пиксельными координатами получаем математические координаты этой точки:

    QPointF q;
    . . .
    R2Point p = mapFromPixels(q);

Метод mapFromPixels используется, например, при получении математических координат точки, отмеченной кликом мыши:

    void DrawArea::mousePressEvent(QMouseEvent* event) {
        . . .
        R2Point p = mapFromPixels(event->pos());
        points[numPoints] = p;
        ++numPoints;
        . . .
    }

Здесь переменная event описывает событие, состоящее в нажатии на клавишу мыши. Точку, в которой это произошло, можно получить, применив к объекту, на который ссылается указатель event, метод pos(), возвращающий точку в пиксельных координатах ("pos" от слова позиция). Можно было бы написать (в старых версиях Qt)

        QPointF q = event->pos();       // Qt4, Qt5

или в современных версиях:

        QPointF q = event->position();  // Qt6

К точке в пиксельных координатах, возвращенной методом pos() класса QMouseEvent, затем применяется метод mapFromPixels класса DrawArea, и мы получаем ту же точку в математических координатах. В старых версиях Qt

        R2Point p = mapFromPixels(event->pos());        // Qt4, Qt5

или в современных версиях

        R2Point p = mapFromPixels(event->position());   // Qt6

Материалы прошлых лет

6.2.6. Список задач для решения

Во всех задачах точки указываются кликами левой клавиши мыши. По клику левой клавиши мыши программа должна нарисовать крестик в отмеченной точке. После того, как пользователь отметит последнюю точку (во всех задачай — третью) и нажмет кнопку Draw в окне, программа должна нарисовать требуемую кривую, не стирая отмеченные точки.

По нажатию кнопки Clear программа должна стереть все ранее определенные точки и кривую, очистить окно и начать все заново.

Нарисовать эллипс по двум его фокусам и точке на эллипсе. (Эллипс — это геометрическое место точек, сумма расстояний от которых до фокусов эллипса постоянна.)
Нарисовать ветвь гиперболы по двум ее фокусам и точке на этой ветви. (Гипербола — это геометрическое место точек, модуль разности расстояний от которых до фокусов гиперболы постоянен.)
Нарисовать параболу по ее фокусу и директриссе. Директрисса (прямая) задается двумя точками. (Парабола — это геометрическое место точек, расстояния от которых до фокуса и директриссы параболы равны между собой.)

7. Интерполяция

Нарисовать график интерполяционного многочлена степени n по заданным точкам (число точек n+1). Точки отмечаются кликами левой клавиши мыши, программа должна рисовать крестики в указанных точках. По нажатию но кнопку Draw программа должна нарисовать график интерполяционного многочлена, построенного по заданным точкам. Координаты x точек должны быть различны. Число точек ограничено: n<16. Для вычисления многочлена следует использовать интерполяционную формулу Ньютона.
По нажатию на кнопку Clear программа должна стереть все точки, очистить окно и начать все заново.
Пользователь отмечает кликами мыши 4 точки A, B, C, D, координаты x которых строго возрастают. Построить график кубического многочлена, обладающего следующими свойствами:
- график проходит через первую и последнюю точки A и D;
- прямая AB задает производную многочлена в точке A, т.е. является касательной к графику в точке A;
- прямая CD задает производную многочлена в точке D, т.е. является касательной к графику в точке D.
Указание: такой кубический многочлен удобно вычислять в форме Ньютона. Обозначим A.x=x₀, D.x=x₁. Нужно найти коэффициенты a_i в представлении многочлена
p(x) = a₀ + a₁(x-x₀) + a₂(x-x₀) (x-x₁) + a₃(x-x₀)² (x-x₁).
Нарисовать кривую Безье порядка n. Кривая Безье порядка n строится по n+1-ой точке
     p₀, p₁, ..., p_n
на плоскости, это отображение отрезка [0, 1] в плоскость R²:
     β_n: [0, 1] → R²
Определение рекурсивное:
     β₀(t) = p₀,
     β₁(t) = β_p₀(t) (1-t) + β_p₁(t) (t),
     . . .
     β_n+1(t) = β_{p₀,...,p_n} (t) (1-t) + β_{p₁,...,p_n+1} (t) t.
Кривая Безье нулевого порядка — это просто точка, первого порядка — отрезок, второго порядка — парабола, третьего — кубическая парабола и т.д.
На плоскости R² задана n+1 точка
P₀, P₁, ..., P_n
где n>1 и координаты x разных точек различны. Эти точки представляют собой измерения некоторой неизвестной линейной функции
f(x) = a x + b,
причем измерения потенциально неточные (со случайными ошибками). Вычислить коэффициенты a, b с помощью метода наименьших квадратов (так, чтобы сумма квадратов отклонений функции от измеренных значений была бы минимальной для данного набора измерений) и нарисовать искомую прямую.

8. Геометрия (множество точек на плоскости)

Во всех задачах отмечается множество точек кликами левой или правой клавиш мыши. Отмеченные точки изображаются крестиками синего или красного цвета. Для окончания ввода надо нажать кнопку Draw в окне. После этого программа должна вычислить и нарисовать требуемую фигуру. При нажатии на кнопку Clear в окне программа должна стереть все точки и фигуру и начать все заново.

Построить выпуклую оболочку точек на плоскости.
Построить круг минимального радиуса, содержащий все заданные точки.
Пользователь отмечает n синих и n красных точек. По окончанию ввода соединить красные точки с синими так, чтобы построенные отрезки не пересекались.
Пользователь вводит кликами левой клавиши мыши последовательность вершин замкнутого многоугольника, возможно, не выпуклого. По окончанию ввода вершин нарисовать многоугольник и его разбиение на треугольники диагоналями (площадь пересечения любой пары треугольников должна быть нулевой).

9. Работа с текстами

Во всех задачах следует использовать командную строку, в которой задаются аргументы программы. Последний аргумент командной строки — это всегда имя входного файла, из которого считывается текст. Результат программы должен выводится в выходной поток (т.е. по умолчанию печататься в консольном окне). Заголовок функции main выглядит так:

    int main(int argc, char *argv[]) {
        . . .

Здесь argc — число аргументов командной строки, argv — массив аргументов. Каждый элемент массива argv является указателем на строку, терминированную нулевым байтом. Первый аргумент, т.е. argv[0] — это всегда имя самой программы (точнее, путь к файлу с программой). Вот пример небольшой программы, которая печатает аргументы своей командной строки (файл "args.cpp"):

    #include <stdio.h>

    int main(int argc, char *argv[]) {
        printf("Command line arguments:\n");
        for (int i = 0; i < argc; ++i) {
            printf("%s\n", argv[i]);
        }
        return 0;
    }

Если эта программа (которая получила имя args после компиляции) запускается с помощью командной строки

    ./args e2e4 e7e5

то она печатает:

    Command line arguments:
    ./args
    e2e4
    e7e5

В ряде задач предполагается, что файл содержит латинские и русские буквы в кодировке UTF-8. В других задачах файл содержит только ASCII-символы.

Кодировка UTF-8

Unicode — это нумерация символов всех языков и алфавитов на планете Земля. Unicode неправильно называть кодировкой, это лишь присвоение символам их численных номеров, при этом не определяется, как именно эти номера хранятся в файле или в памяти компьютера. Номер символа называется кодовой точкой (code point) в терминологии Unicode. В настоящее время в Unicode более миллиона символов и кодовых точек.

Кодировка UTF-8 представляет кодовые точки символов в виде последовательностей байтов. Она обладает неоспоримыми преимуществами по сравнению со всеми существовавшими ранее кодировками и парой несущественных недостатков. Преимущества — совместимость с кодировкой ASCII, которая используется, например, компиляторами большинства языков программирования, независимость от компьютерной архитектуры (Little Endian или Big Endian), возможность включать любые символы (русские и английские буквы, умлауты, иероглифы, математические значки и пр.) в один текст, однозначная интерпретация в любых контекстах. Недостатков два: 1) количество байтов, используемых для записи одного символа, переменное (от 1 до 6); 2) работа с символами и строками в кодировке UTF-8 не поддерживается стандартными библиотеками языков C и C++. Но преимущества намного перекрывают эти недостатки. Уже в настоящее время большая часть страниц в Internet использует кодировку UTF-8. (Придумана она была в 1993 году, но повсеместно использоваться стала лишь недавно, примерно с середины десятилетия 2000-2010.)

Символы в UTF-8 кодируются следующим образом.

ASCII-символы с кодами, меньшими 128, кодируются одним байтом точно так же, как и в кодировке ASCII. Старший (знаковый) бит такого байта равен нулю.
Символ с кодом больше 127 кодируется последовательностью байтов, состоящей из начального байта и одного или нескольких байтов продолжения. По начальному байту определяется, сколько байтов продолжения используется.
Начальный байт имеет следующую структуру в двоичной записи:
```
    11...10*...*
```
Старший бит последовательности символа, не входящего в набор символов ASCII, всегда равен 1 (выше он отмечен красным цветом). Дальше идет последовательность единиц (отмечена синим), длина которой равна количеству байтов продолжения. Эта последовательность заканчивается нулевым битом. Оставшиеся биты начального байта содержат старшие биты кодовой точки.

Например, любая русская буква кодируется двухбайтовой последовательностью, поэтому ее начальный байт имеет вид
```
    110*****
```
Здесь звездочками обозначены любые биты. Итак, начальный байт двухбайтовой последовательности, кодирующей русскую букву, в двоичной записи состоит из префикса 110, за которым следуют 5 произвольных битов, составляющих старшие биты Unicode-номера (кодовой точки) русской буквы. Младшие 6 битов кодовой точки содержатся в байте продолжения. Таким образом, кодовая точка русской буквы состоит из 11 битов.
Любой байт продолжения в двоичной форме начинается с префикса 10, далее следуют 6 битов кодовой точки:
```
    10******
```
Биты двоичной записи кодовой точки записываются в байтах продолжения слева направо, начиная со старших битов в начальной байте последовательности и в первом байте продолжения и заканчивая младшими битами в последнем байте продолжения.

Для примера рассмотрим русскую букву 'А'. Ее кодовая точка — это число 1040 в десятичной записи, или 10000010000 в двоичной. В кодировке UTF-8 код буквы А представляется двумя байтами, которые в шестнацатеричном виде записываются как

    d0 90,

в двоичной записи

    11010000 10010000.

Здесь префиксы начального байта и байта продолжения выделены красным цветом. Оставшиеся биты, составляющие двоичную запись кодовой точки символа А, показаны синим цветом и подчеркнуты.

Пример программы, которая печатает Unicode-номера русских букв (кодовые точки): "ruscodes.cpp" (ее текст набран в кодировке UTF-8). Программа просит ввести номер русской буквы (от 0 до 65) и в ответ печатает саму букву и ее кодовую точку. Исходный текст программы включает строку, набранную в UTF-8, содержащую 66 русских букв в алфавитном порядке, сначала прописные (большие) буквы, затем строчные. В алфавит включена буква Ё. Программа по номеру n выбирает из этой строки 2 байта, составляющих UTF-8 кодировку n-й буквы русского алфавита, и по описанному выше алгоритму выделяет биты кодовой точки и печатает ответ. Вот пример работы программы:

    ./ruscodes
    Number of Russian letter (0-65): 0
    Unicode point of letter А = 1040
    Number of Russian letter (0-65): 1
    Unicode point of letter Б = 1041
    Number of Russian letter (0-65): 5
    Unicode point of letter Е = 1045
    Number of Russian letter (0-65): 6
    Unicode point of letter Ё = 1025
    Number of Russian letter (0-65): 7
    Unicode point of letter Ж = 1046
    Number of Russian letter (0-65): 65
    Unicode point of letter я = 1103

Отсюда видно, что кодовые точки всех русских букв упрядочены по алфавиту, за исключением несчастной буквы Ё.

Список задач

Подсчитать число русских букв, русских слов и общее число строк в файле. Кодировка файла UTF-8.
Напечатать все строки файла, содержащие заданный фрагмент текста. Рассматриваются только ASCII-символы. Фрагмент текста может быть просто словом (составленным из любых символов, кроме пробелов и *) или включать в себя символ * (звездочка) в середине фрагмента. Звездочка означает, что вместо нее может содержаться любая подпоследовательность символов. Фрагмент задается как второй аргумент командной строки; если используется звездочка, то его надо обязательно заключить в двойные апострофы. Например, команда
```
     ./search "M_*PI" /usr/include/math.h
```
должна распечатать все строки файла "/usr/include/math.h", которые содержат фрагмент, начинающийся с префикса "M_" и заканчивающийся суффиксом "PI". (Предполагается, что search — название программы.) Вот результат выполнения этой команды:
```
# define M_PI   3.14159265358979323846  /* pi */
# define M_PI_2 1.57079632679489661923  /* pi/2 */
# define M_PI_4 0.78539816339744830962  /* pi/4 */
# define M_1_PI 0.31830988618379067154  /* 1/pi */
# define M_2_PI 0.63661977236758134308  /* 2/pi */
# define M_2_SQRTPI 1.12837916709551257390  /* 2/sqrt(pi) */
# define M_PIl  3.141592653589793238462643383279502884L /* pi */
# define M_PI_2l 1.570796326794896619231321691639751442L /* pi/2 */
# define M_PI_2l 1.570796326794896619231321691639751442L /* pi/2 */
# define M_PI_4l 0.785398163397448309615660845819875721L /* pi/4 */
# define M_1_PIl 0.318309886183790671537767526745028724L /* 1/pi */
# define M_2_PIl 0.636619772367581343075535053490057448L /* 2/pi */
# define M_2_SQRTPIl 1.128379167095512573896158903121545172L /* 2/sqrt(pi) */
```
В тексте, содержащем русские буквы, заменить их транслитерацией. Например, текст "Русское слово" заменяется на "Rousskoe slovo". Исходный текст считывается из файла, имя которого задано в командной строке, результат выводится в выходной поток. Кодировка файла UTF-8.
Текстовый файл содержит какое-то количество целых констант (запись константы может начинаться со знака "+" или "-" и далее содержать только десятичные цифры). Найти и напечатать их сумму. Кодировка файла ASCII или UTF-8.
Упорядочить строки файла лексикографически по возрастанию. Предполагается, что текст содержит только ASCII-символы.