Мехмат, семестр 4
Программирование

Самостоятельная работа состоит в решении задач по темам, которые обсуждаются в лекциях. По каждой теме нужно решить одну задачу из предлагаемого списка. Номер задачи равен номеру студента в журнале по модулю n, где n — число задач по данной теме.

Весенний семестр 2024-25

  1. Компьютерные сети. Обзор, классификация. Понятие протокола. Уровневая модель описания сетевых протоколов. Примеры протоколов физического уровня (CSMA/CD, Ethernet, Token Ring, DQDB). Стек интернетовских протоколов TCP/IP. Программирование с использованием интерфейса BSDI-сокетов.
  2. Параллельное программирование: нити (потоки, легковесные процессы) и их синхронизация.

Элементы теории чисел

Кодирование с открытым ключом и элементы теории чисел

Содержание лекции:

Презентация: теория чисел в криптографии

Файл numberth.py:
реализация базовых алгоритмов теории чисел на Python

  • Вычисление наибольшего общего делителя двух целых чисел
  • Расширенный алгоритм Евклида — представление наибольшего общего делителя d целых чисел m, n в виде линейной комбинации этих чисел с целыми коэффициентами:

    d = u·m + v·n

  • Вычисление обратного элемента в кольце вычетов по модулю m
  • Алгоритм быстрого воззведения в степень в кольце вычетов по модулю m

Список задач

  1. Реализовать вероятностный тест простоты Миллера-Рабина.
  2. Реализовать алгоритм для Китайской теоремы об остатках.
  3. Факторизовать целое число с помощью ρ-алгоритма Полларда.
  4. Факторизовать целое число с помощью p-1-алгоритма Полларда.
  5. Вычислить квадратный корень из x в поле Zp (p — простое число), т.е. найти r такое, что r2 ≡ x (mod p).
  • Необязательная задача (ее можно выбрать вместо любой из перечисленных выше задач): факторизовать целое число с помощью алгоритма Ленстра на эллиптических кривых.

Классы в Python'е

Презентация: Классы в Python'е на примере классов R2Vector и R2Point для поддержки графики на плоскости R2.
Оба класса содержатся в модуле R2Graph, файл "R2Graph.py".

Еще один несложный пример: класс Zm, реализующий элементы кольца вычетов по модулю m, файл "Zm.py".

Список задач

(в 2024-25 учебном году эти задачи не обязательны).
  1. Реализовать класс Polynomial, представляющий многочлен произвольной степени с коэффициентами в поле рациональных чисел. Должны быть реализованы операции сложения, умножения, деления с остатком, вычисление наибольшего общего делителя многочленов, производной многочлена, а также вычисление многочлена с теми же корнями, свободного от кратных корней, т.е. частного от деления многочлена f на gcd(f, f').

    Указание: в Python'е рациональные числа представлены классом Fraction в модуле fractions. 

        >>> from fractions import *
    >>> x = Fraction(3, 7)
    >>> y = Fraction(1, 5)
    >>> x + y
    Fraction(22, 35)
  2. Та же задача, но для многочленов над полем Zp.
    (Следует в решении использовать класс Zm, реализующий элементы кольца вычетов по модулю m, файл "    Zm.py".)
  3. Реализовать класс "Элементы поля GFp2", где p — простое число.
    См. Конструкция конечного поля из p2 элементов.
    (Следует в решении использовать класс Zm, реализующий элементы кольца вычетов по модулю m, файл "Zm.py".)
  4. Реализовать класс "Матрицы порядка m×n над полем рациональных чисел". Должны быть реализованы операции над матрицами, приведение матрицы к ступенчатому виду, вычисление ранга, а также для квадратной матрицы вычисление определителя и обратной матрицы и решение линейной системы с невырожденной матрицей.
  5. Та же задача, но для матриц над полем Zp.
    (Следует в решении использовать класс Zm, реализующий элементы кольца вычетов по модулю m, файл "Zm.py".)

Работа с матрицами в Python'е. Модуль numpy

В реальных приложениях никто не работает с матрицами большого размера как с базовыми списками Питона (матрица как список строк, каждая строка — список чисел). Связано это с тем, что такая работа с матрицами не очень эффективна. Для представления массивов и матриц (а также многомерных массивов) обычно используют модуль numpy и класс numpy.ndarray. Пример: 

>>> import numpy as np
>>> a = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 0.]])
>>> a
array([[1., 2., 3.],
       [4., 5., 6.],
       [7., 8., 0.]])
>>> type(a)
<class 'numpy.ndarray'>
>>> a.shape
(3, 3)
>>> a[0, 0]
1.0
>>> a[1][0]
4.0
>>> a[1]
array([4., 5., 6.])
>>> a[:,[1]]
array([[2.],
       [5.],
       [8.]])

Задачи на работу с матрицами в Python'е

В 2024-25 учебном году эти задачи не обязательны.

В задании 2 варианта, нужно сделать одну задачу. Студенты с нечетными номерами по журналу делают задачу 1, с четными — задачу 2. Во всех задачах надо реализовать функцию, которая в зависимости от варианта возвращает либо матрицу, либо линейный массив.

В задачах предполагается, что матрицы и линейные массивы представляются numpy-массивами типа numpy.ndarray. Во всех вариантах используйте уже готовую функцию

(rank, det) = gauss(a)
которая приводит матрицу a к ступенчатому виду и возвращает ранг и определитель матрицы (для неквадратной матрицы определитель не вычисляется и возвращается 0). Матрица a представлена в виде двумерного numpy-массива с вещественными значениями. Функция реализована в файле "gauss.py".

Отметим еще раз, что функция не должна ничего печатать (и уж тем более не должна ничего вводить с клавиатуры!). Результатом работы функции должно быть вычисление требуемого объекта, который функция должна возвращать с помощью оператора return. Исходные аргументы функции при этом меняться не должны.

  1. Вычислить обратную матрицу к невырожденной квадратной вещественной матрице: 
        b = inverseMatrix(a)
  2. Решить систему линейных уравнений с невырожденной квадратной вещественной матрицей: 
        x = solveLinearSystem(a, b)
    Здесь a — матрица вещественных чисел, b — массив свободных членов уравнений. Функция должна вернуть массив x вещественных чисел, представляющий решение системы a*x = b.

Отметим, что обе эти задачи реализованы в подмодуле linalg модуля numpy (linalg, возможно, от слов линейная алгебра). Вычисление обратной матрицы к матрице a: 

    ainv = numpy.linalg.inv(a)
Решение системы линейных уравнений a·x = b: 
    x = numpy.linalg.solve(a, b)
Примеры: 
>>> import numpy as np
>>> a = np.array([[1,2,3],[4,5,6],[7,8,0]], dtype="float64")
>>> ainv = np.linalg.inv(a)
>>> ainv
array([[-1.77777778,  0.88888889, -0.11111111],
       [ 1.55555556, -0.77777778,  0.22222222],
       [-0.11111111,  0.22222222, -0.11111111]])
>>> ainv @ a
array([[ 1.00000000e+00, -4.44089210e-16,  0.00000000e+00],
       [ 2.22044605e-16,  1.00000000e+00,  0.00000000e+00],
       [ 1.11022302e-16,  1.11022302e-16,  1.00000000e+00]])
>>> b = np.array([2., 3., 5.])
>>> x = np.linalg.solve(a, b)
>>> x
array([-1.44444444,  1.88888889, -0.11111111])
>>> a @ x
array([2., 3., 5.])
Однако пользоваться функциями из модуля numpy.linalg запрешено, требуется самостоятельно реализовать функции вычисления обратной матрицы и решения системы линейных уравнений.

Графика и оконное программирование на языке Python

Для графики мы используем модуль tkinter, представляющий собой наиболее простой оконный интерфейс. Мы также используем небольшой модуль R2Graph.py, в котором реализованы классы R2Vector и R2Point, с помощью которых удобно решать разные геометрические задачи на плоскости.

Подробный текст лекции: Графика на языке Python

Примеры графических программ, использующих модуль tkinter

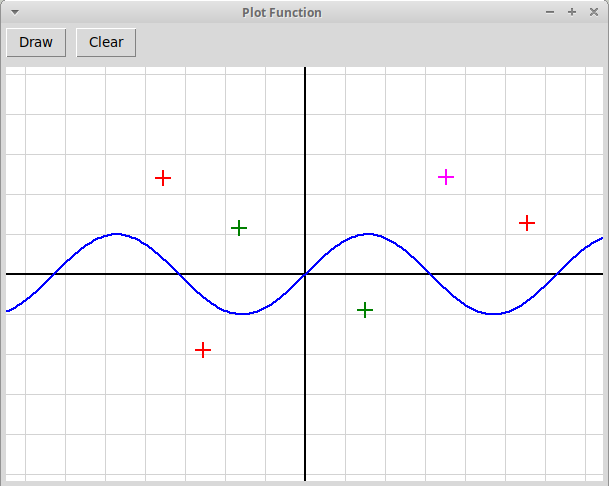
  • Рисование графика функции, заданной в тексте программы, а также точек, отмеченных кликами мыши: plotFunc.py
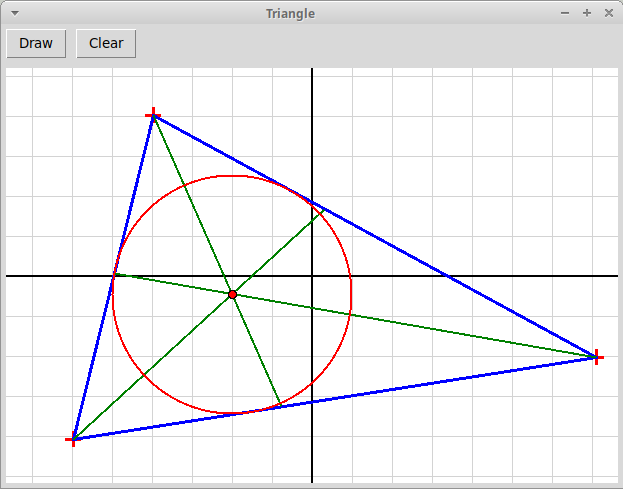
  • Нариcовать треугольник по кликам мыши, а также три его биссектрисы и вписанную окружность: triangle3.py
  • Та же программа "Треугольник", но с возможностью перетаскивания его вершин мышью, при этом картинка меняется в реальном времени: triangle4.py
  • Цифровые часы: dclock.py
  • Аналоговые часы: analogclock.py

Элементы машинного обучения

Задача регрессии и ее решение методом наименьших квадратов

Типичные задачи в машинном обучении — это задачи регрессии и классификации. Мы рассматриваем объекты, каждый из которых задается набором признаков (features), обычно признаки — это просто вещественные числа. Таким образом, объект x — это вектор n-мерного пространства x∈Rn.

В задаче регрессии наша цель — построить функцию, вычисляющую некоторые вещественные значения на объектах:

f: Rn → R,      f(x) = y
Эта функция задается некоторой математической моделью, зависящей от набора параметров — линейной моделью, нейросетью и др. В задаче машинного обучения задана тренировочная база для обучения — набор объектов xi, для которых заданы значения yi этой функции:
x0, x1, ..., xm-1 ∈ Rn
y0, y1, ..., ym-1 ∈ R
f(xi) = yi.
Иногда подобные значения требуемой функции на объектах из тренировочной базы называют разметкой. Требуется подобрать параметры w∈Rk математической модели fw для функции f так, чтобы она на объектах из тренировочной базы принимала значения, как можно более близкие к заданным:
fw(xi) ≈ yi.
Точнее, подбирая набор параметров w∈Rk, мы минимизируем функцию средней ошибки на элементах тренировочной базы (эту функцию также называют функцией потерь, или loss function):
L(w) = 1/m ∑i h(fw(xi), yi) → minw
Здесь h(y1, y2) — функция ошибки на одном элементе, измеряющая отклонение значения y1 от y2. Наиболее популярная функция ошибки — квадрат разности значений (или квадрат нормы разности векторов):
h(y1, y2) = |y1 - y2|2
Общепринятое обозначение для функции средней квадратичной ошибки — MSE (Mean Square Error), или L2 Loss:
MSE(w) = L2(w) = 1/m ∑i |fw(xi) - yi|2
Популярна также функция среднего отклонения по абсолютной величине — MAE (Mean Absolute Error), или L1 Loss:
MAE(w) = L1(w) = 1/m ∑i |fw(xi) - yi|

Описание метода наименьших квадратов.

Домашнее задание

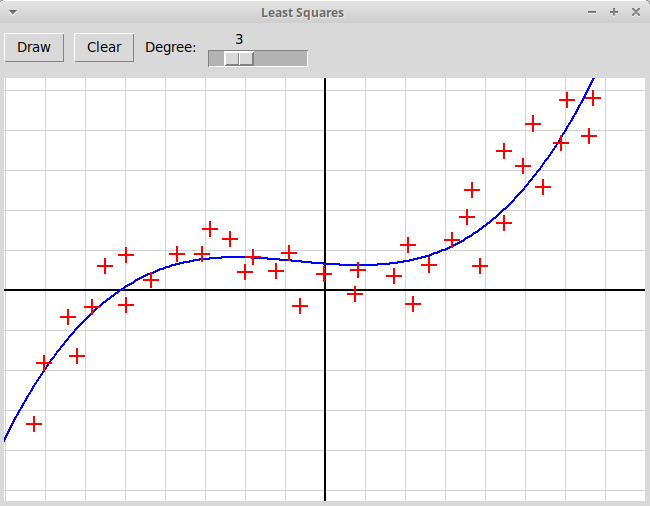
Написать, используя модуль tkinter, оконное графическое приложение, иллюстрирующее метод наименьших квадратов. Пользователь отмечает мышью набор точек на плоскости, программа должна найти многочлен заданной степени, минимизирующий сумму квадратов уклонений значений многочлена от значений, заданных узлами интерполяции:

В качестве образца следует использовать программу, рисующую график интерполяционного многочлена по заданным узлам интерполяции; многочлен вычисляется по формуле Ньютона:

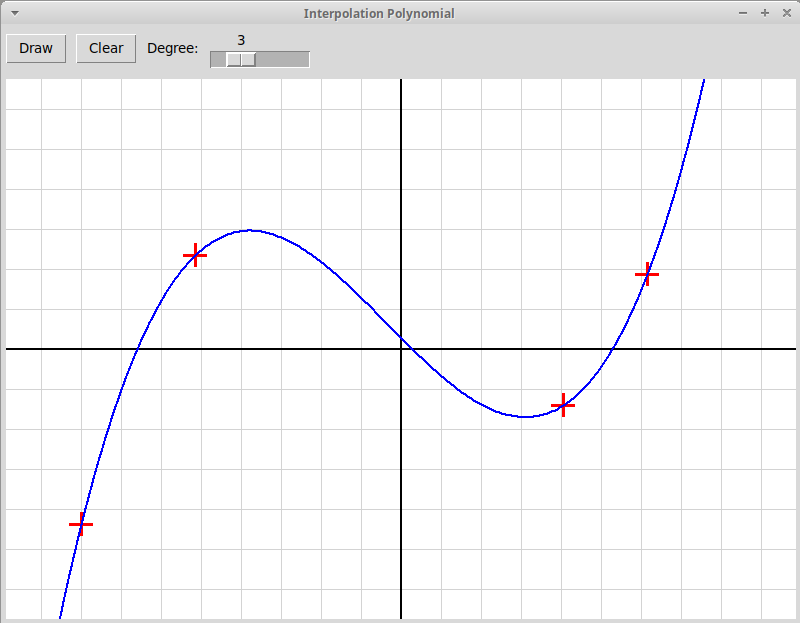
Приложение использует два файла: "newton.py" (оконный интерфейс), "newtonPol.py" (вычисление полинома Ньютона). Архив всех файлов: "newtonInterpol.zip".

Борьба с выбросами в задаче регрессии. Минимизация функции ошибки MAE (средняя абсолютная величина отклонения) методами линейного программирования

В задаче линейной регрессии мы строим зависимость между независимой переменной x∈Rn и зависимой переменной y∈R. Зависимость описывается вектором w∈Rn и свободным членом b∈R:

f(x) = ⟨w, x⟩ + b.
Зависимость строится по тестовой выборке
{ (xi, yi), i=0,…, m-1 }.
В методе наименьших квадратов мы находим параметры модели w, b, минимизируя среднюю кадратичную ошибку MSE (Mean Squared Error). Серьезным недостатком этого метода является сильная зависимость результата от случайных выбросов: из-за возведения разности на каждом измерении в квадрат выбросы значительно больше влияют на суммарную величину ошибки, чем небольшие отклонения от модели при регулярных измерениях. В результате построенная модель имеет тенденцию минимизировать скорее расстояние до выбросов, чем до регулярных точек. Пример приведен на рисунке:

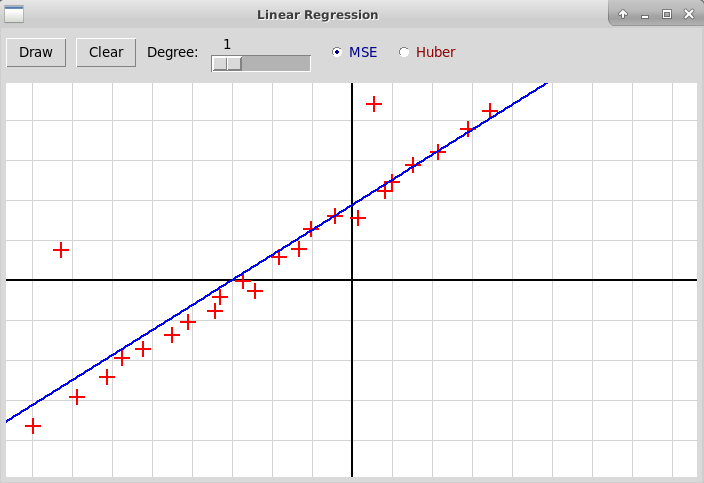
Из-за двух выбросов построенная линия заметно отклоняется от линии, вдоль которой располагаются "регулярные" точки.

Если вместо средней величины квадрата разности минимизировать абсолютную величину разности, то построенная модель будет в значительно меньшей степени зависеть от выбросов. Среднее значение абсолютной величины ошибки обозначается через MAE (Mean Absolute Error):

1/m ∑i|f(xi) − yi| → minw,b

Проблемой является то, что функция модуля не дифференцируема в нуле. Это мешает применять алгоритмы минимизации (градиентный спуск, метод сопряженных градиентов и др.), предполагающие, что минимизируемая функция дифференцируема. Ниже будет рассмотрено использование функции потерь Хубера вместо модуля, которая является как бы компромиссом между квадратичной функцией потерь (квадрат разности двух величин) и модулем разности. Однако задачу минимизации среднего значения абсолютной величины ошибки можно решить и методами линейного программирования.

Трюк с избавлением от модуля

Приведенная формулировка задачи минимизации не позволяет сразу применить методы линейного программирования из-за использования функции модуля. Однако можно применить следующий трюк. Пусть мы минимизируем сумму модулей некоторых величин |ei|, i=0,…,m-1. Каждую величину ei, которая может быть положительной и отрицательной, можно представить в виде разности двух положительных величин:

ei = ui − vi,    ui ≥ 0,   vi ≥ 0.
Тогда для модуля выполняется неравенство:
|ei| ≤ ui + vi.
(модуль суммы не превосходит суммы модулей). Таким образом, мы сводим задачу минимизации модуля |ei| к задаче минимизации суммы двух положительных величин ui + vi. Отметим, что если мы находим минимум суммы в задаче
ei = ui − vi,    ui ≥ 0,   vi ≥ 0,
ui + vi → min,
то тогда либо ui = 0, либо vi = 0 (иначе можно было бы уменьшить обе переменные на одну и ту же величину, при этом их разность не изменилась бы, а сумма уменьшилась). Это означает, что в точке минимума выполняется точное равенство:
|ei| = ui + vi.

Переформулируем задачу линейной регрессии. Во-первых, можно избавиться от свободного члена b, добавив ко всем объектам x дополнительный признак, тождественно равный единице (т.е. еще одну дополнительную координату к каждому вектору). Вместо исходной линейной модели

f(x) = ⟨w, x⟩ + b.
мы будем использовать более простую модель
g(x') = ⟨w', x'⟩,
где
x' = (x, 1) ∈ Rn+1,    w' = (w, b) ∈ Rn+1.

Опустим штрихи в обозначениях x', w', чтобы не загромождать запись. Итак, нам надо минимизировать следующую сумму:

∑i|⟨w, x⟩ − yi| → minw
Введем дополнительные неотрицательные переменные ui, vi, для которых выполняются равенства:
⟨w, x⟩ − yi = ui − vi,
ui ≥ 0,    vi ≥ 0,    i=0,…,m-1.
Теперь нам достаточно минимизировать сумму этих дополнительных переменных. Задача переформулируется следующим образом:
⟨w, x⟩ − yi = ui − vi,
ui ≥ 0,    vi ≥ 0,    i=0,…,m-1,
∑i(ui + vi)   → min
А это уже задача линейного программирования, которая решается стандартными методами.

Линейное программирование в задаче минимизации функции потерь

В Python есть модуль pulp (Python Universal Linear Programming), очень удобный для решения задач линейного программирования. Но, к сожалению, он не установлен на мехмате в компьютерных классах. Но есть также и модуль scipy.optimize, в котором содержится функция linprog, возможно, не такая удобная, но при этом совсем простая. Давайте используем ее.

При вызове этой функции мы указываем набор ограничений типа неравенств, набор ограничемний типа равенств, характеристику переменных — они могут быть совсем свободными, ограниченными с одной стороны (например, неотрицательными) или ограниченными с обеих сторон. Указываем также линейную целевую функцию, которую мы минимизируем. Алгоритм linprog находит точку, в которой целевая функция достигает минимума, используя один из математических методов линейного программирования (симплекс-метод или др.).

Интерфейс функции linprog: 

    res = linprog(c, A_ub=None, b_ub=None, A_eq=None, b_eq=None, bounds=None)
(несколько дополнительных параметров и их значения по умолчанию опущены). Здесь матрица A_ub и вектор-столбец b_ub описывают зависимости типа неравенств (верхних ограничений — upper bounds):
A_ub · X ≤ b_up
Через X мы обозначили вектор-столбец переменных, неравенства векторов должны выполняться покомпонентно. Аналогично матрица A_eq и вектор-столбец b_eq описывают зависимости типа равенств (equalities):
A_eq · X = b_eq

Первый параметр c функции linprog — это вектор коэффициентов линейной функции, которую мы минимизируем:

∑ici xi → minx

Ограничения на переменные описываются списком bounds, содержащим последовательность пар ограничений (xmini, xmaxi) для каждой переменной:

xmini ≤ xi ≤ xmaxi
Если ограничение снизу или сверху отсутствует, то соответствующий элемент пары равен None; в частности, свободная переменная задается парой (None, None), неотрицательная переменная — парой (0, None).

Функция linprog возвращает объект res, в котором, в частности, содержится вектор res.x, минимизирующий целевую функцию при заданном наборе ограничений.

Применим функцию linprog к нашей задаче:

⟨w, x⟩ − yi = ui − vi,
ui ≥ 0,    vi ≥ 0,    i=0,…,m-1,
∑i(ui + vi)   → min
Для этого мы используем следующий фрагмент кода на Python. Здесь points — это массив узлов интерполяции типа R2Point, по которым мы строим аппроксимирующий многочлен степени degree. Каждая точка p в массиве имеет координаты (p.x, p.y). Объект X в нашем случае — это вектор
(xd, xd-1, … x, 1),
где d = degree. Мы ищем коэффициенты
w = (w0, w1, … wd)
аппроксимирующего полинома
w0·xd + w1·xd-1 + … + wd-1·x + wd = ⟨w, X⟩
Вот этот фрагмент кода: 
    m = len(points)
    n = degree + 1
    k = n + 2*m
    a_eq = np.zeros(shape=(m, k))
    x = np.zeros(m)
    for i in range(len(points)):
        x[i] = points[i].x

    v = np.vander(x, n)
    a_eq[:, :n] = v
    for i in range(m):
        a_eq[i, n+2*i] = (-1.)
        a_eq[i, n+2*i+1] = 1.
    b_eq = np.zeros(m)
    for i in range(m):
        b_eq[i] = points[i].y
    bounds = []
    for i in range(n):
        bounds.append((None, None))
    for i in range(n, k):
        bounds.append((0., None))

    # Target loss function
    c = np.zeros(k)
    for i in range(m):
        c[n + 2*i] = 1.
        c[n + 2*i + 1] = 1.
    res = linprog(c, A_eq = a_eq, b_eq = b_eq, bounds = bounds)
    w = res.x[:n]
(см. программу "leastSquares.py", архив всех файлов "leastSquares.zip").

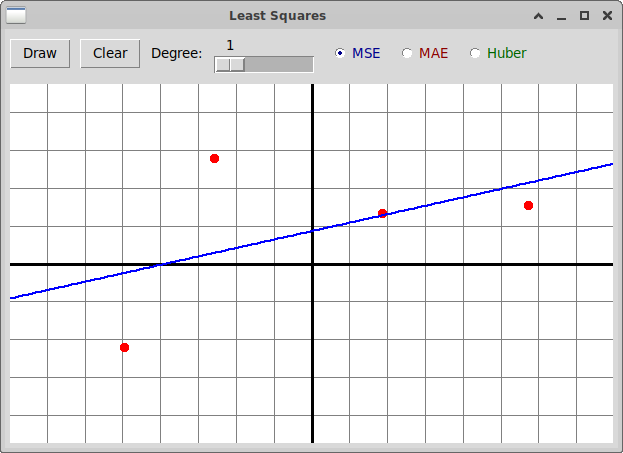
Вот как выглядит применение функций потерь MSE и MAE в программе "leastSquares.py". Рассмотрим множество точек, которые отражают примерно линейную зависимость между переменными x и y, с одним выбросом, заметно влияющим на линию, вычисленную с помощью метода наименьших квадратов (функция потерь MSE):

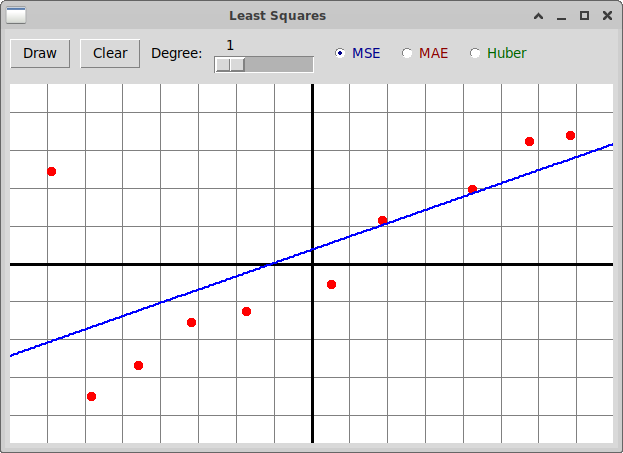
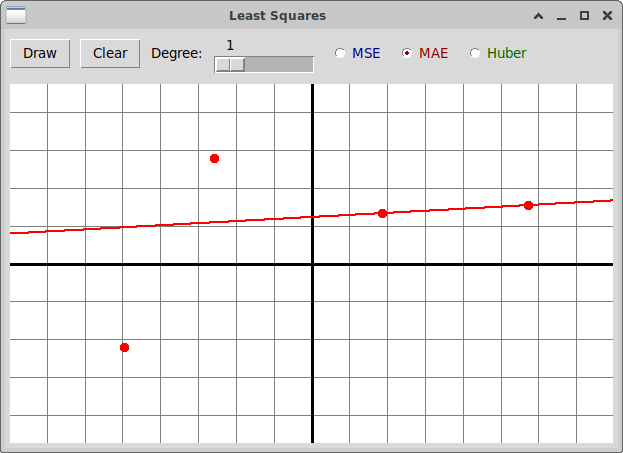
А вот результат вычисления той же линейной зависимости при использовании функции потерь MAE методами линейного программирования:

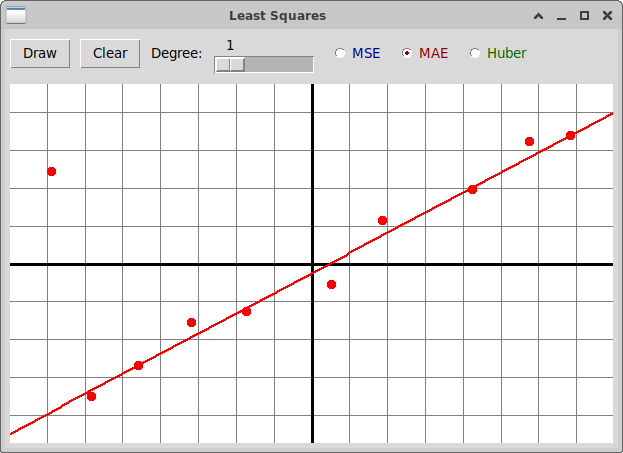
Мы видим, что во втором случае выброс значительно меньше влияет на результат.

Борьба с выбросами в задаче регрессии. Использование функции потерь Хубера

Использование функции потерь Хубера в задаче линейной регрессии

Функция потерь Хубера является как бы компромиссом между функцией потерь MSE, равной среднему квадратичному отклонению, и функцией потерь MAE, равной средней абсолютной величине отклонения. Ведь, с одной стороны, среднее квадратичное отклонение соответствует тому, что ошибки, как правило, распределены по нормальному закону (поскольку ошибка является результатом сложения многих независимых случайных величин, и из центральной предельной теоремы теории вероятностей вытекает, что распределение ошибки близко к нормальному; а плотность вероятности в случае нормального распределения обратно пропорциональна квадрату отклонения). С другой стороны, средне-квадратичная функция потерь очень чувствительна к выбросам и резко растет благодаря возведению в квадрат величины отклонения, из-за чего метод наименьших квадратов имеет тенденцию минимизировать ошибку скорее для выбросов, чем для регулярных точек. Функция потерь MAE нечувствительна к выбросам, но при их отсутствии дает менее точный результат, чем функция MSE.

Очевидное решение следующее: для небольших отклонений мы применяем возведение отклонения в данной точке в квадрат; при больших отклонениях применяем абсолютную величину отклонения. Функции y=x2 и y=|x| в промежуточной точке склеиваются так, чтобы результирующая функция и ее производная были бы непрерывны. Определим для одной точки функцию потерь Хубера, зависящую от параметра δ:

Hδ(x) = {
1/2 ·x2,    |x| ≤ δ,
δ(|x| - δ/2),    |x| > δ.
Для небольших |x| ≤ δ функция Хубера ведет себя как квадрат, при больших |x| > δ — как линейная функция с тангенсом угла наклона δ; при этом функция Хубера всюду дифференцируема.

На следующей картинке изображен график функции Хубера для δ=1 (синий цвет), а также графики функций y = |x| (красный) и y = x2/2 (зеленый):

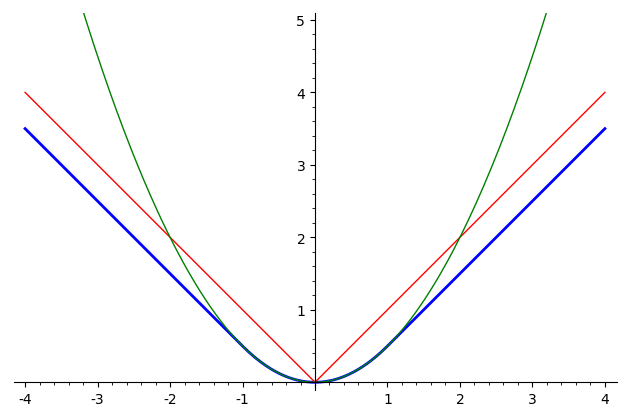
Видно, что функция потерь Хубера объединяет в себе лучшие свойства квадратичной функции ошибки и абсолютной величины ошибки: она всюду дифференцируема и при малых отклонениях ведет себя так же, как и квадратичная функция, но при этом не растет чрезмерно быстро, как и абсолютная величина. В задаче регрессии модель строится путем минимизации функции средней ошибки, вычисление которой использует функцию потери Хубера Hδ(x):

1/m ∑i Hδ(f(xi) - yi) → min

Если при вычислении линейной зависимости применить функцию потерь Хубера к тому же множеству точек, что мы рассмотрели выше, то получим следующий результат:

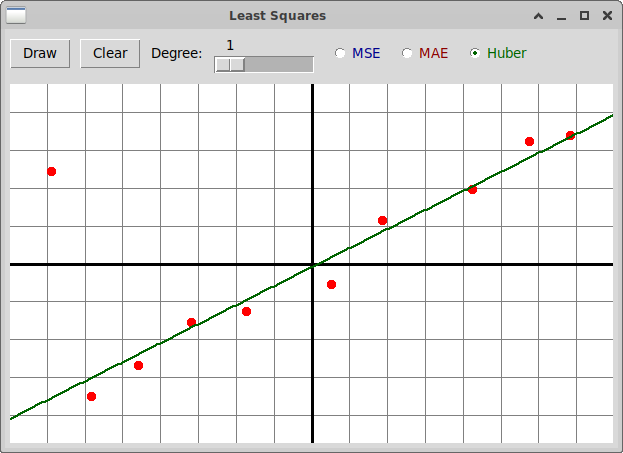
В данном случае он близок к результату, полученному с помощью функции MAE. Но рассмотрим пример, когда функция потерь Huber дает более правильнй результат среди всех трех рассмотренных функций MSE, MAE, Huber:



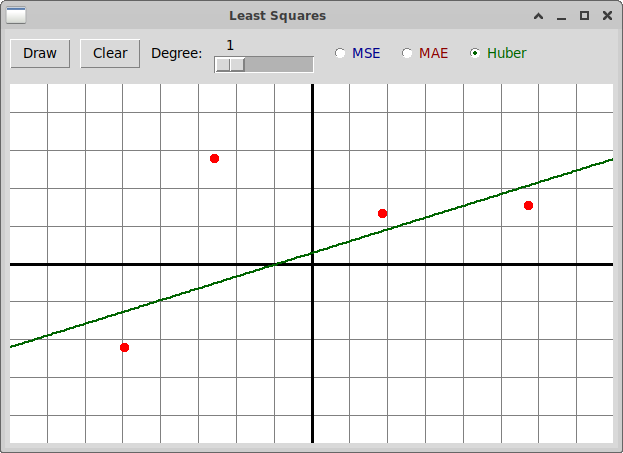
В этом примере вторая слева точка скорее всего является выбросом. Она сильно влияет на результат при применении функции потерь MSE, но и результат применения функции MAE также неудовлетворителен. Наиболее правильный результат достигается именно применением функции Huber.

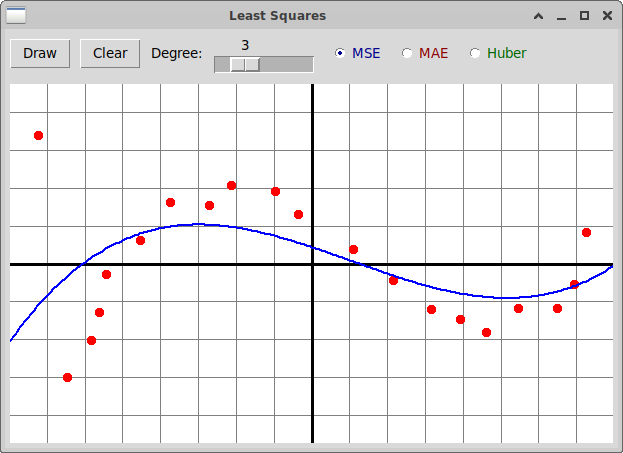
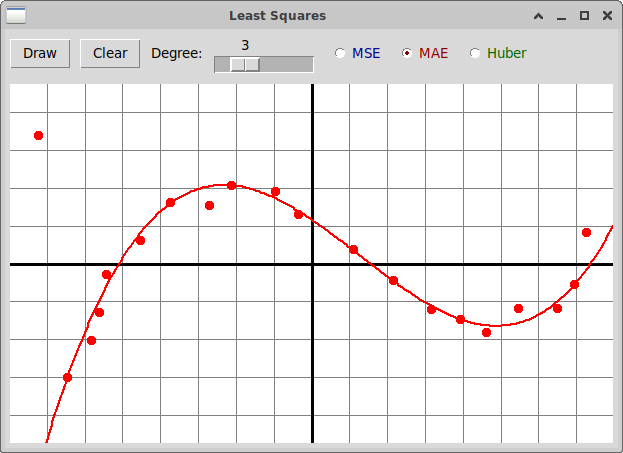
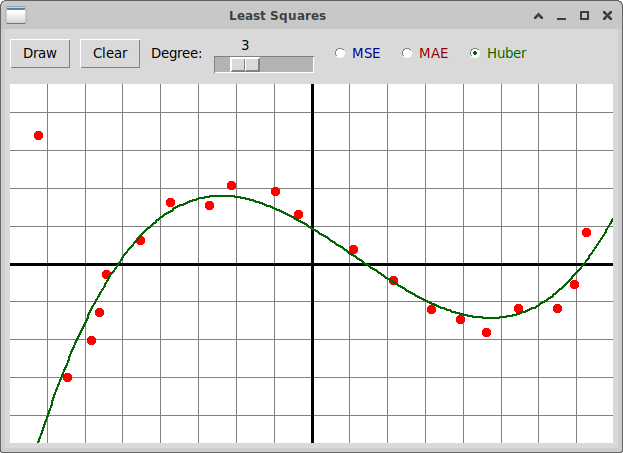
Домашнее задание

В программу "leastSquares.py" добавьте реализацию вычисления полиномиальной зависимости между независимой величиной x и зависящей от нее величиной y методом машинного обучения (путем построения линейной модели) с использованием функции потерь Huber. Вот пример реализации:



В файле "leastSquares.py" часть, относящаяся к использованию функции Huber, специально оставлена не реализованной. Архив всех файлов программы: "leastSquares.zip".

Указание к реализации

В модуле Питона sklearn, посвященному машинному обучению, конечно же, есть реализация построения линейной модели с использованием функции Хубера. Однако от вас требуется реализовать построение модели самостоятельно, используя алгоритм минимизации произвольной функции, который содержится в подмодуле optimize модуля scipy. Функция, вычисляющая минимум другой функции (точку минимума и значение), называется minimize. Таким образом, в начале программы должны быть строки 

import numpy as np
from scipy.optimize import minimize
Обратите внимание, что удобно минимизировать не просто функцию, а функтор! Функтор — это объект, который как бы играет роль функции, т.е. вызывается путем применения к нему круглых скобок. Нужен функтор потому, что минимизируемая функция обычно зависит от множества параметров, которые удобно сохранять внутри объекта-функтора, задавая параметры в конструкторе класса. Например, в нашем случае такими параметрами является массив узлов интерполяции x, степень аппроксимирующего многочлена degree и массив y значений аппроксимируемой функции в узлах. Таким образом, наш функтор можно определить так: 
    class errorFunction:
        def __init__(self, x, degree, y):
            self.x = x
            self.y = y
            self.degree = degree

        def __call__(self, pol):
            m = len(self.x)
            n = self.degree + 1
            res = 0.
            for i in range(m):
                v = np.polyval(pol, self.x[i])
                res += huberFunction(v - self.y[i])
            return res
Напомним, что метод __call__ класса вызывается путем применения круглых скобок, внутри которых передается аргумент функции, в данном случае — массив pol коэффициентов искомого многочлена по убыванию степеней.

Функция потери Хубера определена следующим образом: 

    def huberFunction(x, delta = 1.):
        ax = abs(x)
        if ax < delta:
            return 0.5*ax*ax
        else:
            return delta*(ax - delta*0.5)

Искомый полином вычисляется примерно так. Определим функцию huberPolynomial, вычисляющую массив коэффициентов искомого аппроксимирующего полинома путем минимизации функции потерь Хубера (коэффициенты полинома упорядочиваются по убыванию степеней): 

    def huberPolynomial(x, y, degree):
        m = len(x)
        assert m <= len(y)
        if m == 0:
            return None

        # Initial approximation: polynomial of degree zero
        meanValue = sum(y)/m
        n = degree + 1
        pol = np.zeros(n)
        pol[degree] = meanValue

        res = minimize(fun = errorFunction(x, degree, y), x0 = pol)
        w = res.x
        return w
Здесь стандартная функция minimize из модуля scipy.optimize Питона минимизирует функтор errorFunction(x, degree, y), которому при вызовах передаются коэффициенты аппроксимирующего многочлена. Функции minimize требуется также передать начальное приближение через ее аргумент x0. Мы в качестве начального приближения передаем коэффициенты многочлена требуемой степени degree, у которого свободный член равен среднему значению элементов массива y, а все остальные коэффициенты равны нулю. Функция minimize возвращает в качестве результата объект res, у которого член res.x содержит точку, в которой целевая функция достигает минимума. Объект res содержит также и другие члены, описывающие результаты применения алгоритма минимизации. Для примера см. консольную программу "huberLossFunction.py", которая использует библиотеку Питона matplotlib для рисования графиков. Программа вычисляет два аппроксимирующих многочлена, используя квадратичную функцию потерь и функцию потерь Хубера. Вот результат применения программы для четырех точек, ищем полином первой степени: 
    > python3 huberLossFunction.py

    Enter a degree of polynomial: 1
    Enter the number of nodes: 4
    Enter array of nodes x, y:
    x[0]: -3
    y[0]: -3
    x[1]: -1
    y[1]: 4
    x[2]: 1
    y[2]: 1
    x[3]: 3
    y[3]: 2
    minimization: success = True
        message = Optimization terminated successfully.

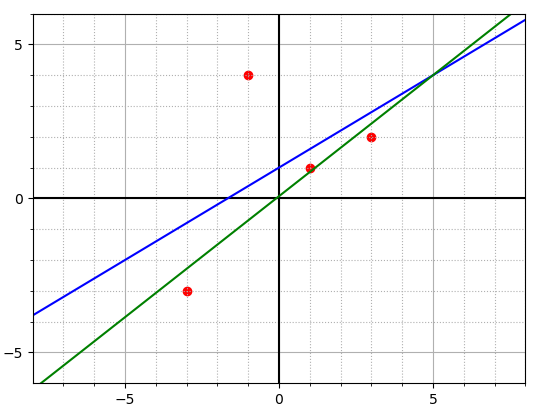
График полинома, вычисленного с помощью минимизации квадратичной функции потерь, нарисован синим цветом, с помощью минимизации функции потерь Хубера — зеленым.