Магистратура мехмата
Специальный компьютерный практикум
Самостоятельная работа состоит в решении задач по темам,
которые обсуждаются в лекциях.
По каждой теме нужно решить одну задачу из предлагаемого списка.
Номер задачи равен номеру студента в журнале по модулю n,
где n — число задач по данной теме.
Решения задач присылайте мне на электронную почту в виде одного или
нескольких файлов, присоединенных к письму (если файлов много,
то лучше присылать zip-архив с файлами в поддиректории).
Адрес моей электронной почты:
vladimir_borisen (собака) mail.ru
Тема письма должна начинаться со слова "Магистратура".
Для дистанционных занятий можно использовать Zoom.
Ссылка на конференцию:
https://us05web.zoom.us/j/2842740990?pwd=bkhtRlNxL3E3SnZCTU1oSFNHcHJNQT09
Passcode: 1
Записи лекций прошлых лет:
осенний семестр 2021
весенний семестр 2022
- Журнал группы магистратуры 1 курса, осенний семестр 2025-26 г.
- Записи лекций прошлого года в текстовом файле ("виртуальная доска").
- Журнал группы магистратуры 1 курса прошлого года, осенний семестр 2024-25 г.
- Записи лекций в текстовом файле прошлого года ("виртуальная доска").
- Журнал группы магистратуры 1 курса, весенний семестр 2024 г.
- Журнал группы магистратуры 1 курса прошлого года, весенний семестр 2023 г.
-
Домашние задания (ссылки)
По каждой теме надо сделать одну задачу в соответствии с номером студента по журналу (номер задачи совпадает с номером студента в журнале по модулю m, где m — число задач в данной теме).
- Задачи на тему "Применение теории чисел в криптографии".
- Задачи на тему "Классы в Python'е".
- Задачи на тему "Модуль numpy и алгоритмы работы с матрицами в Python'е".
- Задача на тему "Линейная регрессия и метод наименьших квадратов.
- Задача на тему "Борьба с выбросами в задаче линейной регрессии": использование функции ошибки Хубера и функции средней абсолютной величины ошибки MAE (вместо функции квадратичной ошибки MSE), в последнем случае с помощью использования методов линейного программирования (модуль pulp Питона).
- Задачи на тему "Модификация классического линейного метода опорных векторов" путем расширения набора признаков (использование всех мономов от исходных признаков степени не выше d) или применения ядрового метода опорных векторов.
- Задачи на тему "Классификация рукописных цифр с помощью ядрового метода опорных векторов и применения метода главных компонент".
Осенний семестр
Весенний семестр
Осенний семестр 2024-25
- Записи лекций прошлого года в текстовом файле ("виртуальная доска").
- Журнал группы магистратуры 1 курса, осенний семестр 2024-25 уч. год
По каждой теме нужно решить одну задачу.
Номер задачи равен номеру студента в журнале по модулю n,
где n — число задач по данной теме.
Решения задач присылайте мне на электронную почту в виде одного или
нескольких файлов, присоединенных к письму (если файлов много,
то лучше присылать zip-архив с файлами в поддиректории).
В теме письма (поле Subject:) должно быть слово "Магистратура".
Адрес моей электронной почты:
vladimir_borisen (собака) mail.ru
Классы в С++
Трехмерная графика и аналитическая геометрия
Классы для поддержки двумерной и трехмерной графики
Лекция 4 сентября 2020. Классы для поддержки двумерной и трехмерной графики и решение с их помощью геометрических задач. Видео.
Для вычислений на плоскости R2 используются классы R2Vector (вектор на плоскости с вещественными координатами) и R2Point (точка на плоскости). В пакете "R2Graph.zip" реализованы все основные операции на плоскости
Простой пример программы, использующей классы R2Point и R2Vector и потоковый ввод-вывод в стиле C++: ввести вершины треугольника и вычислить центр и радиус вписанной окружности. При вычислении запрещено использовать координаты векторов и точек, следует пользоваться исключительно методами классов R2Point и R2Vector. Файл "inCircle.cpp". Программа использует модуль R2Graph, в котором определяются классы для поддержки геометрии на плоскости: файлы "R2Graph.h" и "R2Graph.cpp". Архив всех файлов: "InCircle.zip"
Задачи на использование классов в R2-графике
- Вычислить центр и радиус окружности, описанной вокруг треугольника.
- Вычислить точку пересечения высот треугольника.
-
Вычислить точку Жергона:
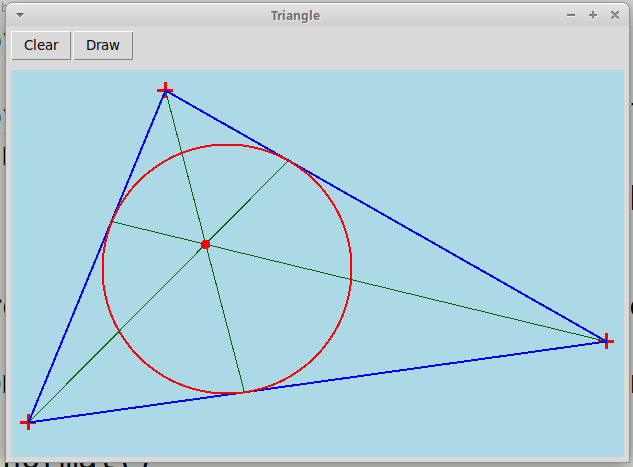
(это точка пересечения чевиан, проведенных из вершин треугольника к точкам касания вписанной окружности).
Трехмерная геометрия: координаты на поверхности Земли и на карте
Мы используем классы R3Vector и R3Point, реализующие точки и векторы трехмерного пространства, для работы с картами земной поверхности. Координаты на поверхности Земли задаются широтой и долготой в градусах. Долгота точки — это угол между плоскостью гринвичского меридиана и плоскостью меридиана, проходящего через данную точку. Широта — это угол между радиус вектором, проведенным из центра Земли в данную точку, и плоскостью экватора. Эти углы измеряются в градусах. Долгота положительна для восточного полушария (и растет по мере продвижения на восток) и отрицательна в западном полушарии. Широта положительна в северном полушарии и отрицательна в южном.
Рассмотрим классическую задачу определения расстояния между двумя точками на поверхности Земли (приблизительно считаем поверхность Земли сферой). Самый простой способ ее решения — это найти угол между радиус-векторами, проведенными из центра Земли к этим точкам, и умножить его на радиус Земли. В классе R3Vector имеется метод angle, возвращающий угол между векторами, мы им воспользуемся. Все, что нам нужно — это реализовать функцию, определяющую радиус-вектор единичной длины, проведенный из центра Земли в направлении заданной точки.
Для представления векторов и точек на поверхности Земли мы используем
декартову систему координат, у которой начало координат расположено
в центре Земли.
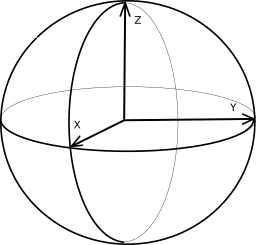 Ось x направлена из центра в точку перечесения
экватора и гринвичского меридиана, ось z направлена на северный
полюс, ось y перпендикулярна осям z и x и направлена
на восток.
Ось x направлена из центра в точку перечесения
экватора и гринвичского меридиана, ось z направлена на северный
полюс, ось y перпендикулярна осям z и x и направлена
на восток.
Радиус-вектор единичной длины, направленный из центра земли
в точку с широтой и долготой (lat, lon),
получается из базисного вектора
ex двумя поворотами: первый поворот на угол lat
выполняеся вокруг оси z, второй поворот на угол lon
выполняется в меридиональной плоскости.
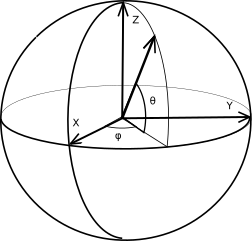 После первого поворота
мы получаем вектор
После первого поворота
мы получаем вектор
R3Vector radiusVector(double lat, double lon) {
double phi = lon*PI/180.; // Convert to radians
double theta = lat*PI/180.;
// Rotate ex around ez by angle phi: v0 = (cos(phi), sin(phi), 0.)
// Rotate v0 in meridional plane by angle theta:
// v1 = (cos(phi)*cos(theta), sin(phi)*cos(theta), sin(theta))
double cosTheta = cos(theta);
return R3Vector(cos(phi)*cosTheta, sin(phi)*cosTheta, sin(theta));
}
(здесь используется константа PI = π, определенная ранее в тексте).
Полный текст программы: "earthdist.cpp". Проект использует также файлы "R3Graph.h" и "R3Graph.cpp", команда для компиляции проекта в Linux'е:
g++ -o earthdist earthdist.cpp R3Graph.cpp
Архив всех файлов:
"earthdist.zip".
Задачи на использование классов в R3-графике

|
Карта представляет собой касательную плоскость к земной сфере. Положение карты задается координатами ее центра: (широта центра, долгота центра). Для представления точек поверхности сферы на карте используется центральная проекция с центром в центре земного шара. На карте используется декартова система координат, в которой ось Y направлена на север (касательная к меридиану, проходящему через центр карты), ось X перпендикулярна оси Y и направлена на восток. Нужно решить одну из следующих двух задач (студенты с нечетными номерами решают 1-ю задачу, с четными — вторую). |
- Заданы координаты центра карты (mlat, mlon) и координаты точки на земной поверхности (lat, lon) в градусах. Получить координаты проекции этой точки на карте (x, y) в метрах.
- Заданы координаты центра карты (mlat, mlon) и координаты точки (x, y) на карте в метрах. Получить координаты точки на поверхности Земли (lat, lon) в градусах, которая проецируется в данную точку на карте.
Реализация классов на C++
Примеры классов, реализующих математические объекты
- Комплексное число: class Complex. Файлы "Complex.h", "Complex.cpp", тестовая программа "complexTst.cpp".
-
Элемент кольца вычетов по модулю m: class Zm.
Файлы "Zm.h",
"Zm.cpp",
тестовая программа
"tstZm.cpp".
Видео лекции 18.09.2020 (вторая половина). - Матрица над полем вещественых чисел: class Matrix. Файлы "Matrix.h", "Matrix.cpp", тестовая программа "matrixTest.cpp".
Задачи по теме "Реализация классов"
В каждой задаче надо реализовать класс, представляющий
некоторый математический объект, и написать программу,
использующую этот класс. Например, реализовать класс Complex
и с помощью этого класса написать программу, решающую
кубическое уравнение (используя формулу Кардано или
другую подобную). В простейшем случае надо хотя бы написать
тестирующую программу, создающие объекты и вызывающую
различные методы класса. Обязательно класс должен быть
описан в отдельном h-файле. Также должен быть cpp-файл,
который реализует сложные (не inline) методы класса.
Например, для класса матриц метод Гаусса приведения матрицы
к ступенчатому виду должен быть реализован в cpp-файле
(ни в коем случае не в h-файле!). Таким образом, проект
должен состоять минимум из трех файлов. Например, тестовый
проект для класса Complex состоит из трех файлов:
Complex.h,
Complex.cpp,
complexTst.cpp.
Также надо написать Makefile, Например, для класса Complex можно в Unix'е или в MAC OS-X использовать файл
CC = g++ $(CFALGS)
# For debugging
CFLAGS = -O0 -g
complexTst: Complex.h Complex.cpp complexTst.cpp
$(CC) -o complexTst complexTst.cpp Complex.cpp
clean:
rm -f complexTst
Архив всех файлов для класса Complex (включая
Makefile):
"Complex.zip".
Список задач по теме "Реализация классов"
-
Реализовать класс Complex, представляющий комплексные
числа. При этом требуется использовать внутреннее представление
комплексных чисел в экспоненциальной форме:
z = r·eiφВоспользовавшись этим классом, написать программу, решающую кубическое уравнение с помощью формулы Кардано (или чего-то похожего). Описание см. в статье Решение кубического уравнения. - Реализовать класс Polynomial, представляющий многочлен произвольной степени с коэффициентами в поле вещественных чисел. Должны быть реализованы операции сложения, умножения, деления с остатком, вычисление наибольшего общего делителя многочленов, производной многочлена, а также вычисление многочлена с теми же корнями, свободного от кратных корней, т.е. частного от деления многочлена f на gcd(f, f').
- Та же задача, но для многочленов над полем Zp.
- Реализовать класс "Элементы поля GFp2", где p — простое число. См. статью Конструкция конечного поля из p2 элементов.
- Реализовать класс "Матрицы порядка m×n над полем вещественных чисел". Должны быть реализованы операции +, -, * над матрицами, приведение матрицы к ступенчатому виду, вычисление ранга, а также для квадратной матрицы вычисление определителя и обратной матрицы и решение линейной системы с невырожденной матрицей.
- Та же задача, но для матриц над полем Zp.
Проект "Стековый калькулятор"
Стековый калькулятор — это калькулятор, память которого представляет собой стек. При выполнении любой операции ее аргументы сначала извлекаются из стека, затем выполняется операция и ее результат добавляется обратно в стек. Таким образом, агрументы операции должны быть положены в стек перед ее выполнением. Программа вычисления значения формулы на стековом калькуляторе соответствует обратной польской записи формулы, в которой знак операции указывается после ее аргументов. Пример:
Ее обратная польская запись: 1, 2, 3, /, +, 4, 56, +, *
Обратную запись формул предложил польский математик Ян Лукасиевич, в его честь она называется польской. Помимо обратной записи, он также предложил и прямую, в которой знак операции указывается перед аргументами. Например, та же формула
Вернемся к обратной польской записи формулы:
+---+ | 1 | | 2 | | 3 | / |2/3| + |5/3| | 4 | |56 | + |60 | * |100|
+---+ | 1 | | 2 | | 1 | +---+ |5/3| | 4 | |5/3| +---+
+---+ | 1 | +---+ +---+ |5/3| +---+
+---+ +---+
Если изначально стек пуст, то по окончании вычисления формулы
глубина стека равна единице, а на вершине стека лежит
значение формулы.
Исходный код проекта "Стековый калькулятор": "StackCalc.zip".
Домашнее задание по проекту "Стековый калькулятор"
Студенты с нечетными номерами по журналу делают первую задачу, с четными — вторую.
-
Добавьте операцию возведения в степень, которая обозначается
значком ^ (крышка) или ** (двойная звездочка), а также возможность
вычисления следующих математических функций:
sin(x), cos(x), exp(x),Последние три функции работают с целыми числами типа long long, при снятии аргументов со стека и при добавлении результата в стек должно выполняться преобразование типов double → long long или long long → double.
log(x) (натуральный), log2(x), log10(x),
tan(x), atan(x), atan2(y, x),
cosh(x), sinh(x), tanh(x),
abs(x), min(x, y), max(x, y), pow(x, y),
powmod(a, n, m), gcd(m, n), invmod(k, m).
-
Воспользовавшись классами R2Vector и R2Point из проекта
"R2Graph.zip", добавьте в стековый
калькулятор следующие команды для решения геометрических задач
на плоскости:
При выполнении команды со стека должны сниматься ее аргументы, после необходимых вычислений в стек должны добавляться ее результаты. Например, при вычислении расстояния от точки до прямой на стеке должны лежать 6 чисел: координаты точки, от которой мы ищем расстояние, координаты точки и направляющего вектора, задающих прямую. Они извлекаются из стека (с учетом порядка, в котором они добавлялись: на вершине стека лежит последний аргумент!), выполняются необходимые вычислния, на стек кладется результат — расстояние от точки до прямой (одно число).
distance Расстояние между двумя точками distanceToLine Расстояние от точки до прямой intersectLines Найти точку пересечения двух прямых inCircle Вычислить окружность, вписанную в треугольник circumCircle Вычислить окружность, описанную вокруг треугольника Помимо добавления результата операции в стек, нужно также напечатать результат выполнения операции (число, точку или окружность). Окружность представляется ее центром и радиусом. В этой задаче обязательно надо использовать модуль "R2Graph.zip" и определенные в нем классы и функции, решение с непосредственными вычислениями через координаты не принимается!
Схема построения цикла с помощью инварианта
Лекция 9 октября 2020.
Схема построения цикла с помощью инварианта и ее применение
на примере ряда алгоритмов: алгоритм Евклида вычисления наибольшего
общего делителя двух целых чисел, алгоритм быстрого возведения в степень,
расширенный алгоритм Евклида, вычисление логарифма с заданной точностью.
Видео лекции.
Исходные тексты перечисленных алгоритмов на C++: файл
"gcd.cpp".
Сортировка
Лекция Алгоритмы сортировки (презентация)
Видео лекции 23 октября 2020: оптимальные алгоритмы сортировки. Сортировка кучей Heap Sort, сортировка слиянием Merge Sort (рекурсивная схема реализации).
Задачи по теме "Сортировка"
В каждой задаче надо реализовать один из оптимальных алгоритмов сортировки, работающих за время O(n log n). При этом уже заданы прототипы функций сортировки, которые надо реализовать. В качестве образца для первых трех задач дается программа "tstSort.cpp", в которой реализованы только функции наивной сортировки (bubbleSort и directSort) и некоторые вспомогательные функции (bubbleDown, merge, printArray), а сами функции сортировки оставлены для самостоятельной реализации — выписаны только прототипы функций сортировки и реализована тестирующая программа. Тестирующая программа генерирует случайной массив вещественных чисел заданной длины, печатает исходный массив, затем вызывает одну из функций сортировки и печатает упорядоченный массив, который получается в результате ее выполнения.
Все функции сортировки могут упорядочивать не весь массив целиком, а некоторый его сегмент. Сегмент задается двумя итераторами first и last: итератор first указывает на начало сортируемого сегмента массива, итератор last — на элемент, которые следует за последним элементом сортируемого сегмента. Функции сортировки должны иметь следующие прототипы:
void heapSort(
std::vector<double>::iterator first, // Beginning of array segment
std::vector<double>::iterator last // After-end of array segment
);
void mergeSortRecursive(
std::vector<double>::iterator first, // Beginning of array segment
std::vector<double>::iterator last, // After-end of array segment
std::vector<double>* tmpMemory = 0 // Temporary memory to use
);
void mergeSortBottomTop(
std::vector<double>::iterator first, // Beginning of array segment
std::vector<double>::iterator last, // After-end of array segment
std::vector<double>* tmpMemory = 0 // Temporary memory to use
);
void radixSort(
std::vector<std::string>::iterator first,
std::vector<std::string>::iterator last,
int compareLength = 64
);
В четвертой задаче надо применить алгоритм RadixSort для сортировки строк ограниченной длины. На вход алгоритму подается массив строк типа std::string и ограничение compareLength на длину строки (точнее, строки могут быть длиннее, чем compareLength, но сравниваются они только по первым compareLength символам). Строки сравниваются лексикографически по их началам длины compareLength (значение по умолчанию 64). Если строка короче, чем compareLength, то она при сравнении мысленно дополняется пробелами справа. Отметим, что в стандартной библиотеке STL языка C++ класс std::string реализует корректно лишь строки ASCII-символов, для символов Unicode этот класс может работать некорректно (в частности, если строка типа std::string содержит последовательность байтов, которые кодируют строку в кодировке UTF-8, то результат побайтового сравнения строк будет некорректным для символов, не входящих в набор ASCII).
Список задач по теме "Сортировка"
Студент должен решить ту задачу, номер которой совпадает по модулю 4 с его номером по журналу.
-
Реализовать алгоритм сортировки кучей Heap Sort. Прототип
функции:
void heapSort( std::vector<double>::iterator first, // Beginning of array segment std::vector<double>::iterator last // After-end of array segment ); -
Реализовать алгоритм сортировки слиянием Merge Sort,
используя рекурсивную схему его реализации.
Прототип функции:
void mergeSortRecursive( std::vector<double>::iterator first, // Beginning of array segment std::vector<double>::iterator last, // After-end of array segment std::vector<double>* tmpMemory = 0 // Temporary memory to use ); -
Реализовать алгоритм сортировки слиянием Merge Sort,
используя восходящую схему его реализации.
Прототип функции:
void mergeSortBottomTop( std::vector<double>::iterator first, // Beginning of array segment std::vector<double>::iterator last, // After-end of array segment std::vector<double>* tmpMemory = 0 // Temporary memory to use ); -
Реализовать алгоритм сортировки Radix Sort
для массива ASCII-строк типа std::string.
Прототип функции:
void radixSort( std::vector<std::string>::iterator first, std::vector<std::string>::iterator last, int compareLength = 64 );Образец тестирующей программы содержится в файле "radixSort.cpp", она содержит код, генерирующий случайные строки, функцию наивной сортировки прямым выбором directSort, а также прототип функции radixSort. Сама функция radixSort в этом файле не реализована, ее нужно реализовать самостоятельно.
Обработка текстов
Функции для работы с символами в кодировке UTF-8: "utf8.h", "utf8.cpp".
Программа нахождения множества русских слов в тексте: "russianWords.cpp". Для каждого слова определяется количество его вхождений в текст. В результате печатается список слов, упорядоченных по количеству вхождений слов в текст, а для слов с одинаковым числом вхождений — лексикографически.
Программа "russianWords.cpp". использует классы std::map, std::basic_string, std::vector и алгоритм std::sort из стандартной библиотеки, а также функции для работы с Unicode-символами в кодировке UTF8 — файлы "utf8.h", "utf8.cpp". Архив всех файлов проекта: "russianWords.zip".
Список задач на тему "Обработка текстов"
- Найти и упорядочить множество пар соседних слов в тексте на русском языке. Два соседних слова образуют пару, если между ними нет знаков препинания и других символов, кроме пробелов, переводов строк и дефисов. Пары слов упорядочиваются по количеству вхождений в текст, а для пар с равным числом вхождений — лексикографически. Напечатать 500 самых часто встречающихся пар.
- Найти и упорядочить множество биграмм в тексте и напечатать их список, упорядоченный по частотам вхождения в текст. (Нужно напечатать только первые 100 биграмм.)
- Реализовать шифр Виженера для текста на русском языке. Шифруются только русские слова, все остальные символы, включая пробелы и переводы строк, исключаются из зашифрованного текста. Ключевая фраза также на русском языке, все прописные буквы заменяются строчными. Должны быть реализованы 2 программы: шифрование и дешифровка.
Программирование в среде Qt
Qt (Quazar Technology) — самая современная и самая лучшая среда для разработки C++ приложений. К достоинствам Qt относятся:
1) независимость текста программы от компьютера и операционной системы — исходные коды приложения одинаковы в Linux, MS Windows, Mac OS-X, и любых других современных операционных системах. В Qt можно создавать программы как для обычных компьютеров (Desktop), так и для операционных систем мобильных телефонов;
2) удобство программирования оконных и параллельных приложений благодаря удачному механизму сигналов и слотов;
3) поддержка огромного набора файловых форматов, сетевых протоколов и устройств;
4) программы на Qt, как правило, намного эффективнее, чем программы, подготовленные в других средах или на других языках, благодаря тому, что исполняющая система Qt автоматически учитывает особенности каждого конкретного компьютера и, к примеру, выбирает самый эффективный метод реализации графики (как правило, через трехмерный интерфейс, если в компьютере есть современная графическая карта);
5) Qt имеет очень удобную среду разработки qtcreator, которая позволяет редактировать оконные формы и добавлять обработчики сигналов, посылаемых управляющими элементами окон; qtcreator синхронно вносит изменения в h- и cpp-файлы.
Qt использует небольшое расширение базового языка C++ — добавлены ключевые слова signal, emit, slot, connect. Сигналы посылаются, например, управляющими элементами окон (для посылки сигнала используется ключевое слово emit). Слоты — это методы, предназначенныедля приема и обработки сигналов. С помощью вызова connect можно связать сигнал, посылаемый некоторым объектом, с обрабатывающим его слотом. При этом обработка выполняется не сразу путем вызова функции, а с помощью постановки сообщения о сигнале в очередь для последующей обработки объектом, принимающим этот сигнал. Такой способ гораздо более гибкий и безопасный, что важно при асинхронной обработке событий в многопоточных программах с параллельным исполнением нескольких нитей. Специальная утилита moc (Meta-Object Compiler) переводит программу с расширения языка С++ на чистый С++. Qt, в отличие от С++ варианта языка CLR-C++ (Сommon Language Runtime), являющегося частью платформы .Net фирмы Microsoft, не использует управляемую динамическую память и сборщик мусора. Благодаря этому Qt-программы быстрее, более надежны и тратят меньше памяти при выполнении, что позволяет использовать их в системах реального времени.
В Qt в основном разрабатываются оконные графические программы. Примеры программ, разработанных с помощью Qt:
-
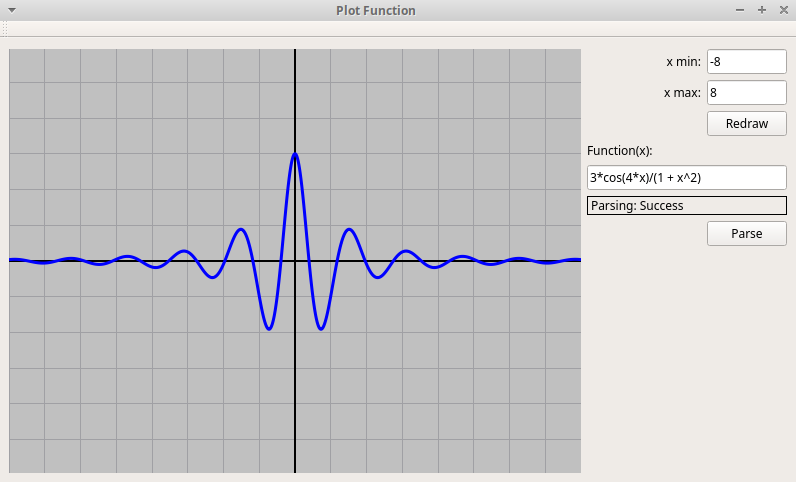
Qt-проект "График функции":
PlotFunc.zip.
В программе реализовано рисование графика произвольной функции от переменной x. Функция задается формулой, которая записывается в текстовом поле окна. Проект включает в себя парсер формул от одной или двух переменных x, y, получающий по текстовой записи формулы ее обратную польскую запись, которая затем используется для вычисления значений функции.
-
Qt-проект "Интерполяционный полином Ньютона":
NewtonPol.zip.
По точкам, отмеченным кликами мыши, строится график интерполяционного многочлена. Удобно использовать интерполяционный многочлен в форме Ньютона:pn(x) = a0 + a1(x-x0) + a2(x-x0)(x-x1) + a3(x-x0)(x-x1)(x-x2) + . . .
+ an(x-x0)(x-x1)(x-x2)...(x-xn-1)Многочлен pn(x) степени n строится по узлам интерполяции x0, x1, x2, ..., xn, в которых он принимает значения y0, y1, y2, ..., yn; коэффициенты многочлена вычисляются последовательно по формуле
an+1 = (yn+1 - pn(xn+1)) / ((xn+1 - x0)(xn+1 - x1)...(xn+1 - xn))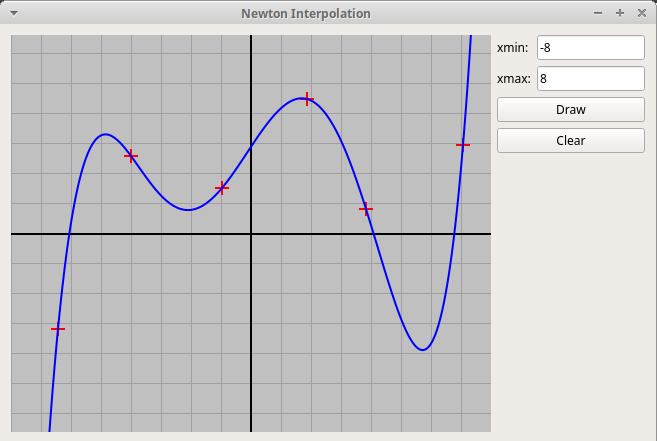
-
Qt-проект "Треугольник":
"Triangle.zip".
По трем точкам, отмеченных кликами мыши, изображается треугольник, его три биссектрисы и вписанная окружность:
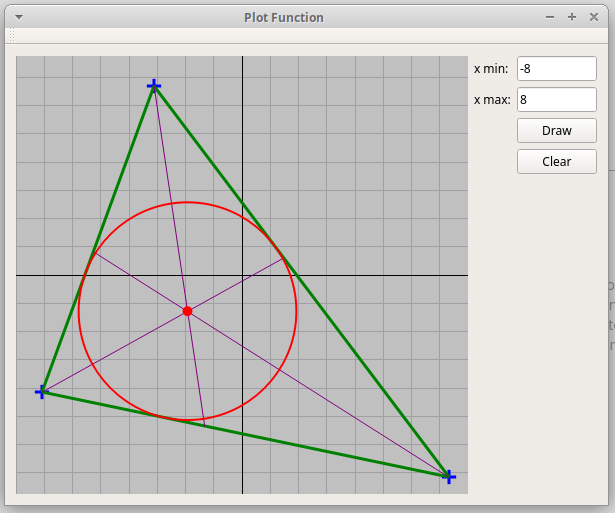
Вершины треугольника можно перетаскивать мышью на новую позицию, при этом картинка изменяется в реальном времени. -
Qt-проект "Часы" (QClock):
"QClock.zip".
Проект иллюстрирует методы рисования, в частности, закрашивание многоугольников (это стрелки часов), изображение текста в окне (цифры на циферблате), определение текущего времени для данной временной зоны, работу с радио-кнопками (для выбора временно́й зоны) и, главное, анимацию в окне (движение стрелок):

Задачи на тему Qt
В задаче 1 надо использовать в качестве образца проект "График функции" PlotFunc.zip. В частности, следует использовать реализованный в нем парсер формул, который по формуле, зависящей от переменных x, y, получает ее обратную польскую запись; обратная польская запись формулы затем используется для вычисления значений формулы для конкретных численных значений переменных x, y. Формула может включать числовые константы, знаки арифметических операций, круглые скобки, стандартные математические функции (sin, cos, exp, log, atan, sqrt, ...), а также операцию возведения в степень ^.
В задачах 3-6 надо нарисовать треугольник, задаваемый кликами мыши, и одну из замечательных точек треугольника, определяемых как пересечение чевиан. Нарисовать надо не только саму точку (в виде маленького закрашенного кружка), но и процесс ее построения.
В качестве образца следует использовать Qt-проект "Triangle.zip".
Список задач
-
Задана функция f(x, y).
(Функция задается в текстовом поле Qt-окна приложения,
запись функции можно редактировать.)
Нарисовать ее линию уровня (изогипсу),
задаваемую уравнением
f(x, y) = 0.
Идея реализации. Разбиваем плоскость на маленькие треугольники. Для каждого треугольника вычисляем значение функции в его вершинах. Если значения одного знака, то линия не пересекает треугольник. Иначе имеем одну вершину одного знака и две вершины другого знака => используя линейную интерполяцию, вычисляем две точки на сторонах треугольника, в которых функция принимает значение 0. Получаем отрезок. Линии уровня состоят из этих отрезков. -
Нарисовать кривую Безье, построенную по узлам, которые пользователь
отмечает кликами мыши. Также реализовать возможность перетаскивания
мышкой отмеченных раньше узлов на новую позицию, при этом уже построенная
по этим узлам кривая Безье должна изменяться в реальном времени.
Кривая Безье B(t) — это отображение числового отрезка [0, 1] в плоскость R2:
B: [0, 1] → R2Кривая Безье порядка n задается n+1 узломp0, p1, ..., pn.Кривая нулевого порядка (построеная по одному узлу) — это просто точка. Кривая Безье B(t) порядка n, построенная по узлам p0, p1, ..., pn, определяется рекурсивно через две кривые B0(t) и B1(t) порядка n-1; кривая B0(t) строится по узламp0, p1, ..., pn-1,кривая B1(t) — по узламp1, p1, ..., pn,Кривая Безье порядка n задается рекурсивно формулой:B(t) = B0(t)·(1-t) + B1(t)·t.Также можно вычисить кривую Безье, используя биномиальные коэффициенты
:С k n B(t) = ∑kБиномиальные коэффициенты вычисляются с помощью треугольника Паскаля
(1-t)n-k tk pkС k n 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 . . .по формуле
=С k n+1
+С k n С k-1 n На картинках ниже изображены кривые Безье, построенные по трем и четырем узлам:
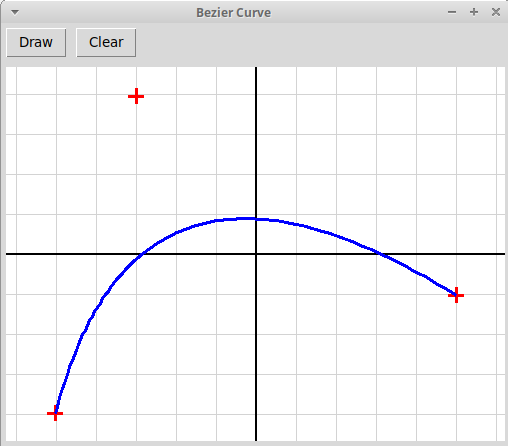
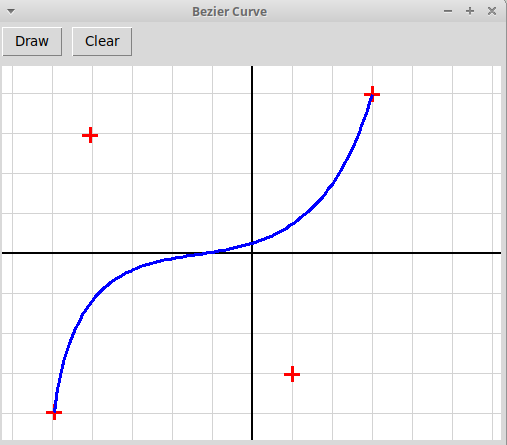
-
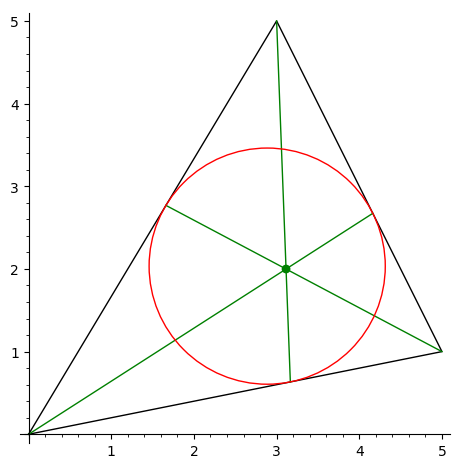
Нарисовать треугольник и точку Жергона —
пересечение отрезков, соединяющих
вершины треугольника с точками касания
вписанной окружности.
-
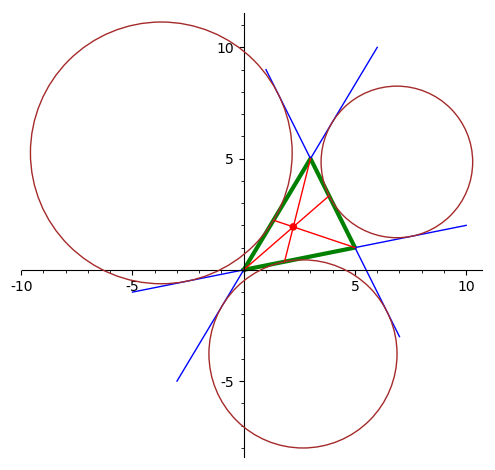
Нарисовать треугольник и точку Нагеля —
пересечение отрезков, соединяющих
вершины треугольника с точками касания
трех внешне вписанных окружностей.
-
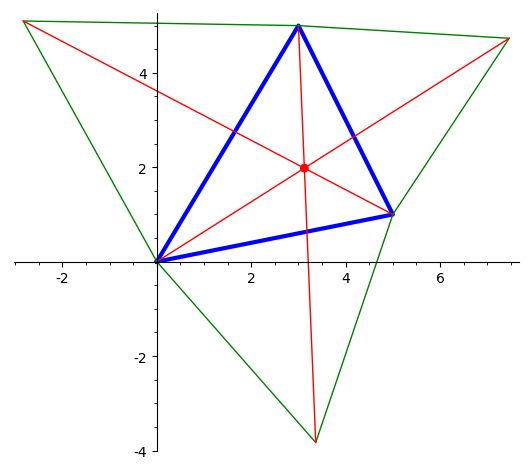
Нарисовать треугольник и точку Лемуана
— точку, изогонально
сопряженную центру тяжести треугольника.
Она определяется как пересечение
симмедиан. Симмедиана — это
отрезок прямой, симметричной медиане
треугольника относительно бисектриссы,
проведенной из той же вершины.
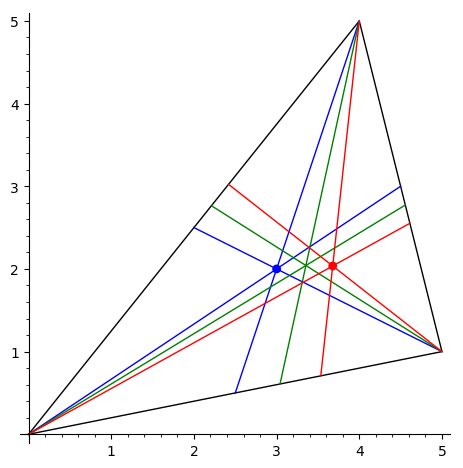
На рисунке синяя точка — это пересечение медиан треугольника. Медианы изображены синим цветом, биссектрисы — зеленым, симмедианы — красным. Точка Лемуана изображена красным кружком. -
Нарисовать треугольник и точку Ферма-Торричелли,
а также процесс ее построения.
Точка Ферма-Торричелли определяется как точка, сумма расстояний от
которой до вершин треугольника минимальна.
Если треугольник не тупоугольный или его тупой угол меньше 120 градусов,
то это точка внутри треугольника, из которой каждая сторона
видна под углом 120 градусов; иначе это вершина
тупого угла.
Весенний семестр 2024 г.
Записи лекций прошлого года (весеннй семестр 2022)
Записи лекций позапрошлого года (весенний семестр 2021)
Тема 1. Язык программирования Python
Журнал группы магистратуры 1 курса, весенний семестр 2024 г.
По каждой теме нужно решить одну задачу.
Номер задачи равен номеру студента в журнале по модулю n,
где n — число задач по данной теме.
Решения задач присылайте мне на электронную почту в виде
файла, присоединенного к письму (*.py для программ
на языке Python3, *.sage для программ на языке sage).
Адрес моей электронной почты:
vladimir_borisen (собака) mail.ru
В теме письма (поле Subject:) должно быть слово "Магистратура".
Тема 1. Язык программирования Python
1.0. Python: задачи для разминки
Примеры программ на языке Python:- разложение числа на множители: factor.py
- печать счастливых билетов длины n: luckyTickets.py
- алгоритмы теории чисел: numTheory.py
Домашнее задание 1 (прошлый год)
В задании 3 варианта, надо сделать ту задачу, номер которой совпадает по модулю 3 с номером студента по журналу.
- Написать функцию для числа счастливых билетов длины n, которая будет работать разумное время по крайней мере для n ≤ 12.
-
Написать функцию, проверяющую, является ли число m полусовершенным.
Число m совершенное, если оно равно сумме своих собственных
делителей. Примеры:
6 = 1 + 2 + 3Число m называется ПОЛУсовершенным, если оно равно сумме какого-то ПОДМНОЖЕСТВА своих собственных делителей.
28 = 1 + 2 + 4 + 7 + 14Указание: следует
1) найти список d всех собственных делителей числа m;
2) решить задачу о рюкзаке napsack(d, m).Задача о рюкзаке
Имеется рюкзак объема m и список вещей, содержащий объемы каждой вещи. Можно ли какими-то вещами из этого списка (не обязательно всеми) заполнить рюкзак доверху?d = [1, 2, 5, 3, 7, 11] m = 10 Можно ли из этого списка выбрать числа, сумма которых равна 10? 2, 5, 3 3, 7 1, 2, 7Эта задача NP-полная и для нее не существует хорошего решения, кроме как полного перебора всех подмножеств. Но, если не искать самого быстрого решения, то она легко решается, например, применением рекурсии. -
Реализовать функцию nextPermutation(s),
на вход подается список чисел, на выходе этот список изменяется.
Функция возвращает True, если перестановка была не последней,
и False, если следующей перестановки нет.
Используется следующий алгоритм:
1) находим, идя с конца перестановки к началу, максимальную возрастающую последовательность в конце перестановки (в примере выделена красным);
6, 3, 1, 2, 10, 4, 9, 12, 11, 8, 7, 52) для предшествующего к ней элемента x (в примере x=9, выделен синим) находим минимальный элемент y возрастающей последовательности, больший x (в примере y=11, отмечен подчеркиванием);
6, 3, 1, 2, 10, 4, 9, 12, 11, 8, 7, 53) меняем местами элементы x и y и затем упорядочиваем элементы в конце перестановки, следующие за элементом y (для этого используем метод sort для отрезка списка, следующего за y).6, 3, 1, 2, 10, 4, 11, 5, 7, 8, 9, 12
1.1. Элементы теории чисел
Кодирование с открытым ключом и элементы теории чиселСодержание лекции:
- Кольцо вычетов по модулю m
- Малая теорема Ферма, китайская теорема об остатках, теорема Эйлера
- Основные алгоритмы теории чисел: алгоритм Евклида, расширенный алгоритм Евклида, быстрое возведение в степень, алгоритм в китайской теореме об остатках, извлечение квадратного корня в поле вычетов по модулю p.
- Тест простоты Ферма и кармайкловы числа
- Вероятностный тест простоты Миллера-Рабина
- Кодирование с открытым ключом, схема RSA
- Алгоритмы факторизации (разложения числа на множители): ρ-алгоритм Полларда и p-1 алгоритм Полларда.
Презентация: теория чисел в криптографии
Файл numberth.py:
реализация базовых алгоритмов теории чисел на Python
- Вычисление наибольшего общего делителя двух целых чисел
-
Расширенный алгоритм Евклида — представление наибольшего
общего делителя d целых чисел m, n
в виде линейной комбинации этих чисел с целыми коэффициентами:
d = u·m + v·n
- Вычисление обратного элемента в кольце вычетов по модулю m
- Алгоритм быстрого воззведения в степень в кольце вычетов по модулю m
Список задач
- Реализовать вероятностный тест простоты Миллера-Рабина.
- Реализовать алгоритм для Китайской теоремы об остатках.
- Факторизовать целое число с помощью ρ-алгоритма Полларда.
- Факторизовать целое число с помощью p-1-алгоритма Полларда.
- Вычислить квадратный корень из x в поле Zp (p — простое число), т.е. найти r такое, что r2 ≡ x (mod p).
- Необязательная задача (ее можно выбрать вместо любой из перечисленных выше задач): факторизовать целое число с помощью алгоритма Ленстра на эллиптических кривых.
1.2. Классы в языке Python
Презентация:
Классы в Python'е
на примере классов R2Vector и R2Point для поддержки графики
на плоскости R2.
Оба класса содержатся в модуле R2Graph,
файл "R2Graph.py".
Еще один несложный пример класса: класс Zm, реализующий элементы кольца вычетов по модулю m, файл "Zm.py".
Список задач
-
Реализовать класс Polynomial, представляющий многочлен
произвольной степени с коэффициентами в поле рациональных
чисел. Должны быть реализованы операции сложения, умножения,
деления с остатком, вычисление наибольшего общего делителя
многочленов, производной многочлена, а также вычисление
многочлена с теми же корнями, свободного от кратных корней,
т.е. частного от
деления многочлена f на gcd(f, f').
Указание: в Python'е рациональные числа представлены классом Fraction в модуле fractions.
>>> from fractions import * >>> x = Fraction(3, 7) >>> y = Fraction(1, 5) >>> x + y Fraction(22, 35) -
Та же задача, но для многочленов над полем Zp.
(Следует в решении использовать класс Zm, реализующий элементы кольца вычетов по модулю m, файл "Zm.py".) -
Реализовать класс "Элементы поля GFp2",
где p — простое число.
См. Конструкция конечного поля из p2 элементов.
(Следует в решении использовать класс Zm, реализующий элементы кольца вычетов по модулю m, файл "Zm.py".) - Реализовать класс "Матрицы порядка m×n над полем рациональных чисел". Должны быть реализованы операции над матрицами, приведение матрицы к ступенчатому виду, вычисление ранга, а также для квадратной матрицы вычисление определителя и обратной матрицы и решение линейной системы с невырожденной матрицей.
-
Та же задача, но для матриц над полем Zp.
(Следует в решении использовать класс Zm, реализующий элементы кольца вычетов по модулю m, файл "Zm.py".)
1.3. Работа с матрицами в Python'е. Модуль numpy
Из программы прошлых лет
Матрица в Питоне обычно представляется списком строк, где каждая строка — это список чисел. Например,
>>> a = [[1, 2, 3], [4, 5, 6], [7, 8, 0]]
>>> print(a)
[[1, 2, 3], [4, 5, 6], [7, 8, 0]]
Замечательная особенность Питона состоит в том, что в нем реализованы целые числа неограниченного размера. Это позволяет реализовать также и рациональные числа. Реализация рациональных чисел с помощью целых чисел типа int или long long в языке C++ бессмысленна, т.к. при арифметических действиях с рациональными числами их знаменатели растут очень быстро и почти сразу наступает переполнение. В Питоне переполнений не бывает. Рациональные числа представлены в Питоне классом Fraction в модуле fractions:
>>> from fractions import *
>>> a = Fraction(1, 3)
>>> print(a)
1/3
>>> b = Fraction(1, 4)
>>> print(b)
1/4
>>> print(a + b)
7/12
Рациональные числа типа Fraction позволяют использовать точную арифметику и получать точный результат, в отличие от вещественных чисел типа float. Например, для типа float бессмыслено сравнивать числа на точное равенство, результат непредсказуем:
>>> a = 1/3
>>> a
0.3333333333333333
>>> b = 1/4
>>> b
0.25
>>> a + b
0.5833333333333333
>>> 7/12
0.5833333333333334
>>> 1/3 + 1/4 == 7/12
False
Неожиданный результат! Для вещественных чисел, представленных типом
float, сумма 1/3 + 1/4 не равна 7/12 (отличие мизерное,
но точного равенства нет).
Для матриц над полем рациональных чисел в Питоне можно реализовать метод Гаусса приведения матрицы к ступенчатому в точности так, как этот метод рассматривается в курсе математики. Это позволяет с помощью программ на Питоне решать задачи, которые обычно даются первокурсникам на практических занятиях в курсе алгебры или линейной алгебры: приведение матрицы к ступенчатому виду, вычисление определителя матрицы, решение систем линейных уравнений, вычисление обратной матрицы и т.п.
Отметим, что для матриц из вещественных чисел метод Гаусса имеет свои особенности: во-первых, мы не можем просто считать элемент равным нулю, поскольку точных равенств при работе с элементами типа float не бывает! Поэтому мы считаем элемент матрицы нулевым, если его абсолютная выличина не превосходит маленького числа eps, например, eps = 1e-8:
>>> (1/3 + 1/4) - 7/12 == 0
False
>>> eps = 1e-8
>>> abs((1/3 + 1/4) - 7/12) <= eps
True
Во-вторых, в методе Гаусса при приведении матрицы к ступенчатому
виду нельзя выбирать произвольный ненулевой разрешающий элемент в столбце.
Если мы выберем маленький ненулевой элемент, то при делении на него
строка в результате будет умножаться на очень большое число,
что приводит к экспоненциальному росту ошибок округления
и неустойчивости алгоритма.
В результате вместо правильного (или близкого к правильному)
ответа мы будем получать просто мусор! Надо обязательно выбирать элемент,
максимальный по абсолютной величине в столбце, чтобы при делении на него
строка умножалась на коэффициент, не превосходящий единицы.
В файле matrix.py реализована работа с матрицами на полем рациональных чисел (тип Fraction) и над полем вещественных чисел (тип float). Функция echelonFormOfRationalMatrix(a) приводит матрицу рациональных чисел к ступенчатому виду и возвращает пару (ступенчатый вид матрицы, ранг матрицы), при этом сама матрица a не изменяется (действия производятся с копией матрицы). Функция showRationalMatrix(a) преобразует объект "матрица" к текстовому виду так, чтобы потом матрицу можно было красиво напечатать:
>>> from matrix import *
>>> a = [[1, 2, 3], [4, 5, 6], [7, 8, 0]]
>>> print(showRationalMatrix(a))
[1 2 3]
[4 5 6]
[7 8 0]
>>> (b, rank) = echelonFormOfRationalMatrix(a)
>>> print(showRationalMatrix(b))
[ 1 2 3]
[ 0 -3 -6]
[ 0 0 -9]
Аналогичные функции echelonFormOfRealMatrix(a) и showRealMatrix(a) реализованы для вещественных матриц:
>>> a = [[1, 2, 3], [4, 5, 6], [7, 8, 0]]
>>> (b, rank) = echelonFormOfRealMatrix(a)
>>> print(showRealMatrix(b))
[ -7.0000 -8.0000 -0.0000]
[ -0.0000 -0.8571 -3.0000]
[ 0.0000 0.0000 4.5000]
Кроме того, в модуле matrix.py
реализованы функции вычисления определителя матрицы,
умножения матриц, а также выполнение элементарных преобразований
и копирование матриц.
Модуль numpy
В реальных приложениях, однако, никто не работает с матрицами большого размера как с базовыми списками Питона (матрица как список строк, каждая строка — список чисел). Связано это с тем, что такая работа с матрицами не очень эффективна. Для представления массивов и матриц (а также многомерных массивов) обычно используют модуль numpy и класс numpy.ndarray. Пример:
>>> import numpy as np
>>> a = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 0.]])
>>> a
array([[1., 2., 3.],
[4., 5., 6.],
[7., 8., 0.]])
>>> type(a)
<class 'numpy.ndarray'>
>>> a.shape
(3, 3)
>>> a[0, 0]
1.0
>>> a[1][0]
4.0
>>> a[1]
array([4., 5., 6.])
>>> a[:,[1]]
array([[2.],
[5.],
[8.]])
Задачи на работу с матрицами в Python'е
В задании 2 варианта, нужно сделать одну задачу. Студенты с нечетными номерами по журналу делают задачу 1, с четными — задачу 2. Во всех задачах надо реализовать функцию, которая в зависимости от варианта возвращает либо матрицу, либо линейный массив.
В задачах предполагается, что матрицы и линейные массивы представляются numpy-массивами типа numpy.ndarray. Во всех вариантах используйте уже готовую функцию
Отметим еще раз, что функция не должна ничего печатать (и уж тем более не должна ничего вводить с клавиатуры!). Результатом работы функции должно быть вычисление требуемого объекта, который функция должна возвращать с помощью оператора return. Исходные аргументы функции при этом меняться не должны.
-
Вычислить обратную матрицу к невырожденной квадратной
вещественной матрице:
b = inverseMatrix(a) -
Решить систему линейных уравнений с
невырожденной квадратной вещественной матрицей:
x = solveLinearSystem(a, b)Здесь a — матрица вещественных чисел, b — массив свободных членов уравнений. Функция должна вернуть массив x вещественных чисел, представляющий решение системы a*x = b.
Отметим, что обе эти задачи реализованы в подмодуле linalg модуля numpy (linalg от слов линейные алгоритмы). Вычисление обратной матрицы к матрице a:
ainv = numpy.linalg.inv(a)
Решение системы линейных уравнений a·x = b:
x = numpy.linalg.solve(a, b)
Примеры:
>>> import numpy as np
>>> a = np.array([[1,2,3],[4,5,6],[7,8,0]], dtype="float64")
>>> ainv = np.linalg.inv(a)
>>> ainv
array([[-1.77777778, 0.88888889, -0.11111111],
[ 1.55555556, -0.77777778, 0.22222222],
[-0.11111111, 0.22222222, -0.11111111]])
>>> ainv @ a
array([[ 1.00000000e+00, -4.44089210e-16, 0.00000000e+00],
[ 2.22044605e-16, 1.00000000e+00, 0.00000000e+00],
[ 1.11022302e-16, 1.11022302e-16, 1.00000000e+00]])
>>> b = np.array([2., 3., 5.])
>>> x = np.linalg.solve(a, b)
>>> x
array([-1.44444444, 1.88888889, -0.11111111])
>>> a @ x
array([2., 3., 5.])
Однако пользоваться функциями из модуля numpy.linalg запрешено,
требуется самостоятельно реализовать функции вычисления обратной матрицы
и решения системы линейных уравнений.
1.4. Графика и оконное программирование на языке Python
Для графики мы используем модуль tkinter, представляющий собой наиболее простой оконный интерфейс. Мы также используем небольшой модуль R2Graph.py, в котором реализованы классы R2Vector и R2Point, с помощью которых удобно решать разные геометрические задачи на плоскости.
Подробный текст лекции: Графика на языке PythonПримеры графических программ, использующих модуль tkinter
-
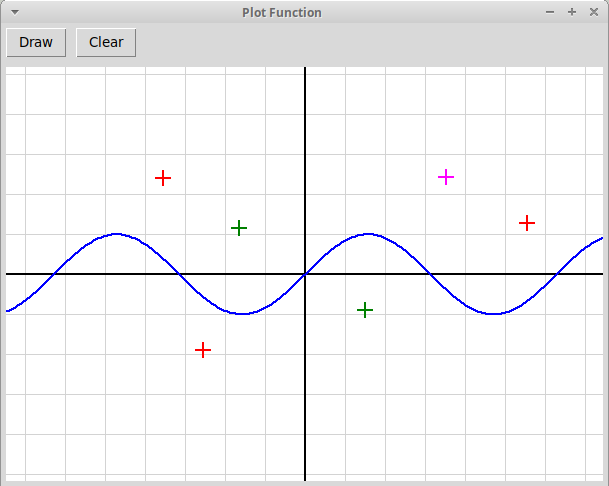
Рисование графика функции, заданной в тексте программы,
а также точек, отмеченных кликами мыши:
plotFunc.py
-
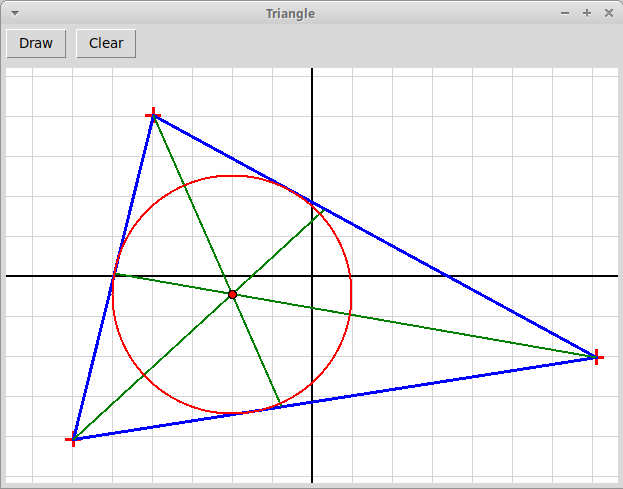
Нариcовать треугольник по кликам мыши, а также
три его биссектрисы и вписанную окружность:
triangle3.py
-
Та же программа "Треугольник", но с возможностью
перетаскивания его вершин мышью, при этом картинка
меняется в реальном времени:
triangle4.py
-
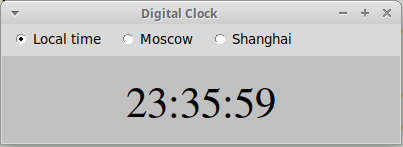
Цифровые часы: dclock.py
-
Аналоговые часы: analogclock.py

1.5. Элементы машинного обучения. Задача регрессии. Метод опорных векторов
1.5.1. Задача регрессии и ее решение методом наименьших квадратов
Описание метода наименьших квадратов.
Домашнее задание
Написать, используя модуль tkinter, оконное графическое приложение,
иллюстрирующее метод наименьших квадратов.
Пользователь отмечает мышью набор точек на плоскости,
программа должна найти многочлен заданной степени,
минимизирующий сумму квадратов уклонений значений многочлена
от значений, заданных узлами интерполяции:
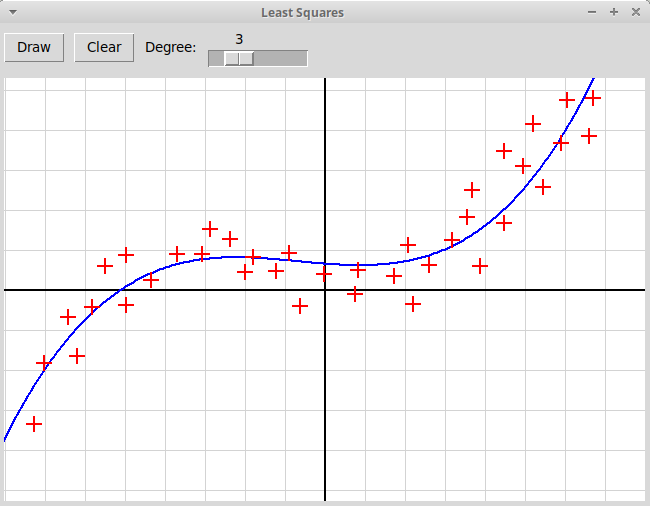
В качестве образца следует использовать
программу, рисующую график интерполяционного многочлена
по заданным узлам интерполяции; многочлен вычисляется по формуле
Ньютона:
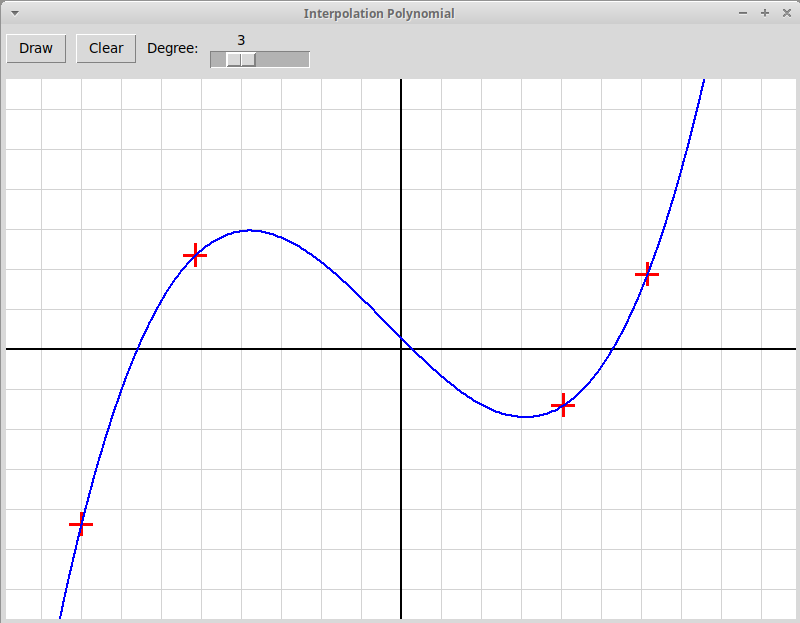
Приложение использует два файла:
"newton.py" (оконный интерфейс),
"newtonPol.py" (вычисление полинома Ньютона).
Архив всех файлов:
"newtonInterpol.zip".
1.5.2. Борьба с выбросами в задаче регрессии. Использование функции потерь Хубера
Использование функции потерь Хубера в задаче линейной регрессии.
1.5.3. Борьба с выбросами в задаче регрессии. Минимизация функции ошибки MAE (средняя абсолютная величина отклонения) методами линейного программирования
Использование методов линейного программирования в задаче регрессии.
Домашнее задание
Дополнить программу
"huberRegression.py",
которая вычисляет линейную регрессию, используя либо
метод наименьших квадратов (т.е. минимизируя
квадратичную функцию ошибки MSE), либо минимизируя функцию
ошибки, определенную с помощью функции Хубера.
Архив всех файлов программы:
"huberRegression.zip".
В программе надо дополнительно реализовать третий способ
вычисления параметров регрессии, который минимизирует
среднюю величину абсолютной ошибки MAE, используя методы
линейного программирования. Модифицированная программа
должна выглядеть примерно так:
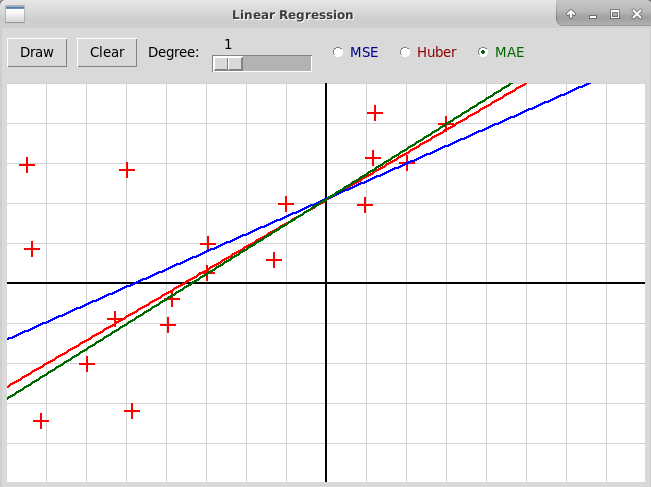
На приведенном скриншоте по заданным узлам
строится прямая, т.е. полином степени 1.
Синим цветом нарисована прямая, построенная методом наименьших
квадратов, красным — с использованием функции Хубера,
зеленым — с помощью минимизации функции MAE
методом линейного программирования.
Можно также построить полином большей степени, например, третьей
(степень полинома задается с помощью слайдера):
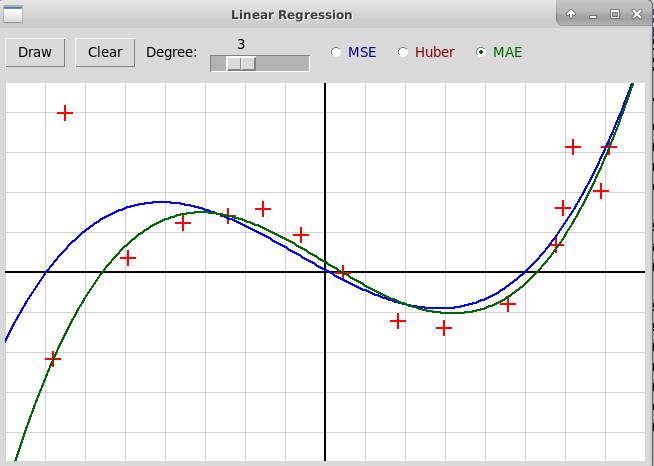
Здесь синяя кривая построена методом наименьших
квадратов, зеленая —
методом линейного программирования. Видно, что во втором случае
влияние выбросов на форму кривой значительно меньше.
Красная кривая, построенная с использованием функции Хубера, здесь не
показана, потому что она в данном случае почти совпадает
с зеленой кривой и на картинке две кривые почти полностью
накладываются друг на друга.
1.5.4. Метод опорных векторов, классический линейный вариант
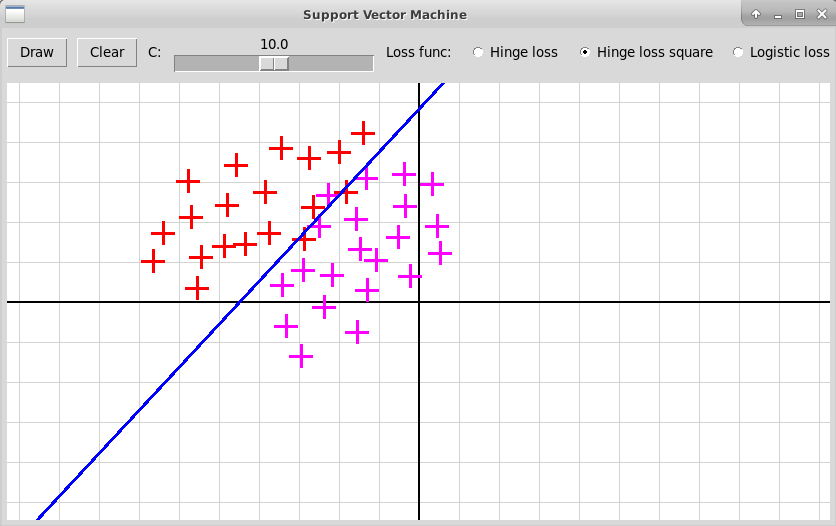
Описание метода опорных векторов (Support Vector Machine)
1.5.5. Нелинейный метод опорных векторов
В классическом методе опорных векторов мы имеем два класса объектов, каждый объект описывается n признаками, представляемыми вещественными числами. Таким образом, объекты x1, x2, … xk представляются точками n-мерного пространства; координаты такой точки равны значениям признаков объекта. В тренировочной выборке объекты xi первого класса отмечены значением yi = 1, объекты xj второго класса — значением yj = -1. В методе опорных векторов SVM (Support Vector Machine) строится линейный классификатор f(x), который определяется как гиперплоскость, разделяющая два класса точек:
x, w ∈ Rn, b ∈ R.
В классическом методе опорных векторов далеко не всегда можно разделить
гиперплоскостью два класса точек в n-мерном пространстве:
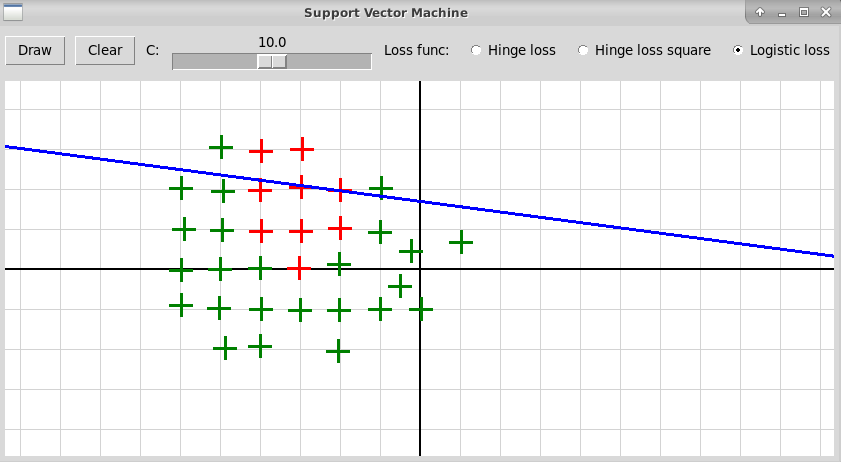
Идея нелинейного метода опорных векторов состоит в том, чтобы дополнить
исходный набор из n признаков объекта дополнительными признаками,
которые вычисляются как некоторые функции от набора исходных признаков.
В результате мы получим
множество точек в пространстве более высокой размерности, где каждая точка
представляет расширенный набор признаков исходного объекта. Можно надеяться,
что в пространстве более высокой размерности эти точки уже можно
разделить гиперплоскостью.
Итак, пусть отображение
φ(x) = (φ1(x), φ2(x), … φm(x)), где x = (x1, x2, … xn),
В простейшем случае в качестве функций φ1(x1, … xn), φ2(x1, … xn), …, φm(x1, … xn) можно взять всевозможные мономы степени не выше d от переменных x1, x2, … xn (то есть от исходных признаков).
Пусть, например, d = 2. Пусть число исходных признаков n = 2, т.е. объекты представляются точками плоскости R2. Тогда расширенный набор признаков представляется всеми мономами степени не выше 2 от переменных x1, x2:
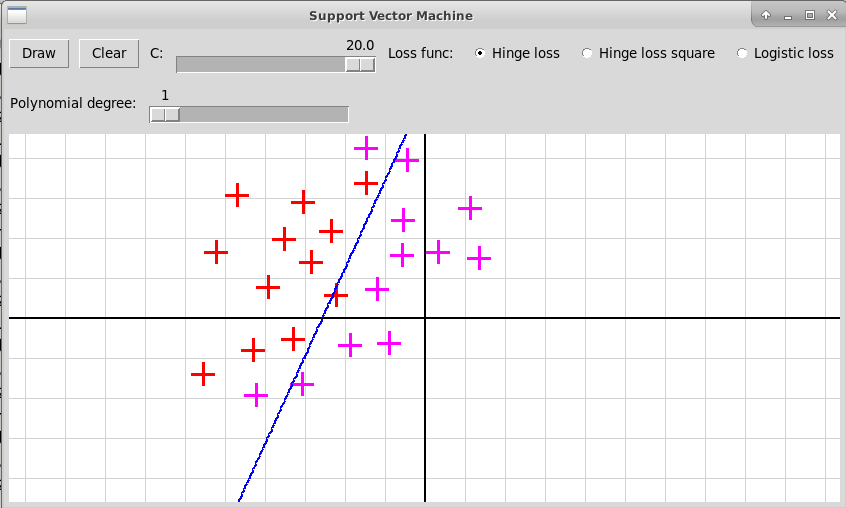
Программа "svmNonlinear.py" иллюстрирует использование нелинейного метода опорных векторов. Исходные объекты представляются точками плоскости двух цветов, отмечаемые кликами левой и правой клавиш мыши. В качестве расширенных признаков используются все мономы степени не выше d от координат x и y очередной точки; степень d задается с помощью слайдера в пределах от 1 до 5. Программа после построения нелинейного классификатора f(x) изображает линию нулевого уровня функции
Классический случай: степень 1
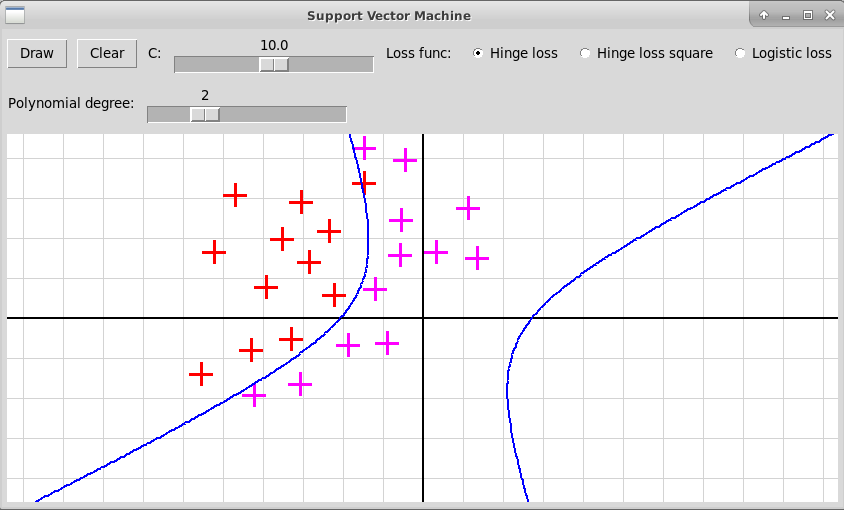
Квадратичные мономы: степень 2
Кубический многочлен: степень 3
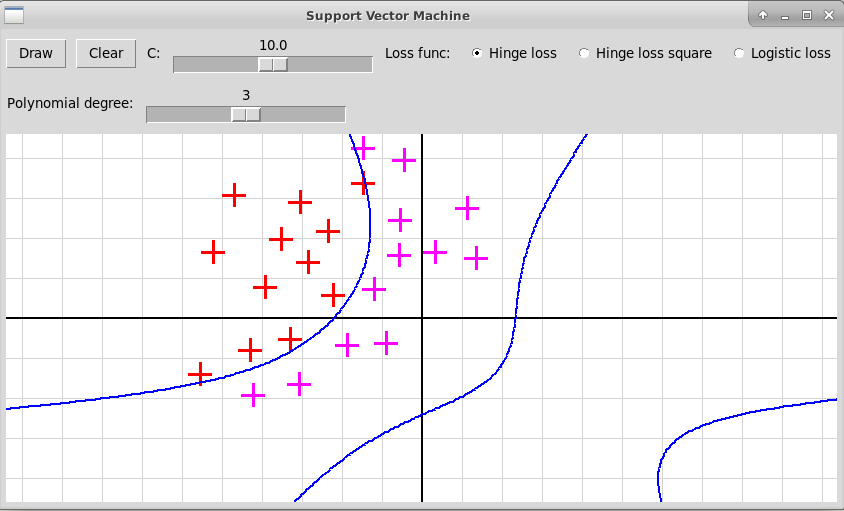
Многочлен степени 4
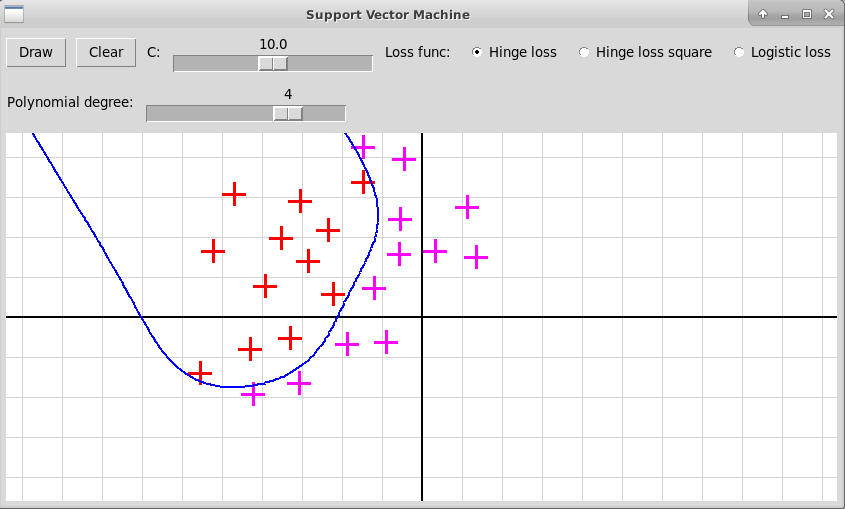
Многочлен степени 5
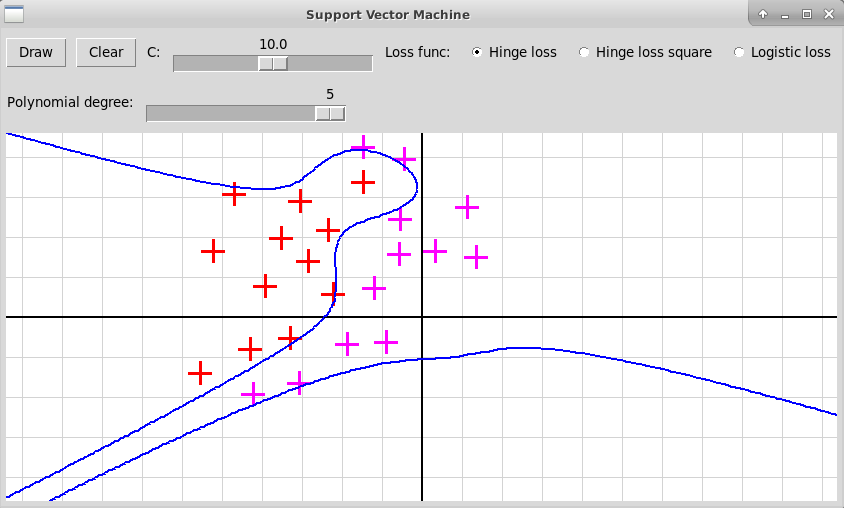
В случае полинома высокой степени 5 мы, скорее всего, наблюдаем переобучение. Также форма разделяющей кривой сильно заисит от гиперпараметра С и от функции потери.
Программа на Питоне (подготовленная в Jupyter-Lab), иллюстрирующая нелинейный метод опорных векторов
# Non-linear Support Vector Machine method
from scipy.optimize import minimize
import numpy as np
import itertools
import random
from math import sin, cos
import matplotlib.pyplot as plt
from skimage import measure
get_ipython().run_line_magic('matplotlib', 'inline')
plt.axes(aspect="equal")
def monomials(x, degree=1):
m = [1.]
for d in range(1, degree+1):
for c in itertools.combinations_with_replacement(x, d):
m.append(np.prod(c))
return np.array(m)
m1 = 100
class1 = [ np.array([
random.normalvariate(1., 1.5), random.normalvariate(1., 0.5)
]) for i in range(m1) ]
m2 = m1
angle1 = -np.pi*2/3
angle2 = np.pi*2/3
ex = np.array([1., 0.]); ey = np.array([0., 1.])
class2 = []
for i in range(m2):
phi = random.normalvariate(0., 1.)
r = random.normalvariate(5., 0.5)
p = ex*cos(phi)*r + ey*sin(phi)*r
class2.append(p.copy())
x = class1 + class2
x = np.array(x)
y = [1.]*len(class1) + [-1.]*len(class2)
y = np.array(y)
m = len(x)
perm = np.random.permutation(m)
x = x[perm]
y = y[perm]
plt.scatter(
[c[0] for c in x], [c[1] for c in x],
color=[ "r" if yy > 0. else "g" for yy in y ]
)
degree = 3
xext = np.array([monomials(xx, degree) for xx in x])
n = len(xext[0])
print("n =", n)
C = 10. # Hyperparameter
w = np.array([0.]*n)
b = 0.
def hingeLoss(c):
return max(1. - c, 0.)
def errorFunction(wb):
w = wb[:-1]
b = wb[-1]
w2 = w @ w
s = 0.
m = len(xext)
for i in range(m):
c = y[i]*(w @ xext[i] - b)
s += hingeLoss(c)
return w2 + (C/m)*s
def classifier(p):
pext = monomials(p, degree)
return w @ pext - b
res = minimize(errorFunction, np.zeros(n + 1))
w = res.x[:-1]
b = res.x[-1]
print("w =", w)
print(" b =", b)
# Draw the separating line
xmin = min([xx[0] for xx in x]) - 1.
xmax = max([xx[0] for xx in x]) + 1.
ymin = min([xx[1] for xx in x]) - 1.
ymax = max([xx[1] for xx in x]) + 1.
rows = 100
cols = rows
def xcoord(j):
dx = (xmax - xmin)/cols
return xmin + j*dx
def ycoord(i):
dy = (ymax - ymin)/rows
return ymin + i*dy
# a is a matrix of dimension (rows, cols)
a = np.array([[0.]*steps for iy in range(rows)])
for i in range(rows):
for j in range(cols):
xx = np.array([xcoord(j), ycoord(i)])
a[i, j] = classifier(xx)
nullContours = measure.find_contours(a, 0.)
for c in nullContours:
plt.plot(
[xcoord(cc[1]) for cc in c],
[ycoord(cc[0]) for cc in c],
color="blue"
)
Вот результат работы этой программы (запущенной в среде Jupyter-Lab):
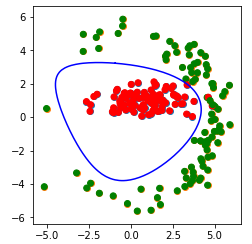
Исходный код программы:
"svmNonlinear.ipynb".
Эта же программа иллюстрирует изображение линий уровня (изолиний, изогипс) функции от двух переменных
# Drawing Isolines
import numpy as np
import matplotlib.pyplot as plt
from skimage import measure
get_ipython().run_line_magic('matplotlib', 'inline')
plt.axes(aspect="equal")
def f(x, y):
return ((x - 2) + (y - 1))**2/4 + ((x - 2) - (y - 1))**2
xmin = -5.; xmax = 10.
ymin = -5.; ymax = 10.
m = 100; n = 100
def xcoordinate(j):
dx = (xmax - xmin)/n
x = xmin + j*dx
return x
def ycoordinate(i):
dy = (ymax - ymin)/m
y = ymin + i*dy
return y
a = np.array([[0.]*n for i in range(m)])
for i in range(m):
y = ycoordinate(i)
for j in range(n):
x = xcoordinate(j)
a[i, j] = f(x, y)
for l in range(20):
level = 0.1*(2**l)
contours = measure.find_contours(a, level)
for c in contours:
plt.plot(
[ xcoordinate(cc[1]) for cc in c ],
[ ycoordinate(cc[0]) for cc in c ]
#, color="blue"
)
Вот результат работы этой программы (запущенной в среде Jupyter-Lab):
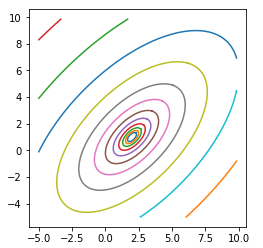
Ядровые методы и их использование в нелинейном методе опорных векторов
Когда мы заменяем обычное скалярное произведение некоторым ядром, представляющим собой скалярное произведение векторов, составленных из набора базисных функций от исходных признаков, то в результате решения задачи минимизации функции потерь мы получаем нелинейный классификатор. При этом, несмотря на увеличение размерности пространства признаков, сложность вычислений остается такой же, как и в случае исходной линейной задачи.
Описание ядрового варианта метода опорных векторов
Вот несколько скриншотов оконной программы на Python+tkinter,
иллюстрирующей применение ядрового метода опорных векторов:
Гауссовское ядро (RBF)
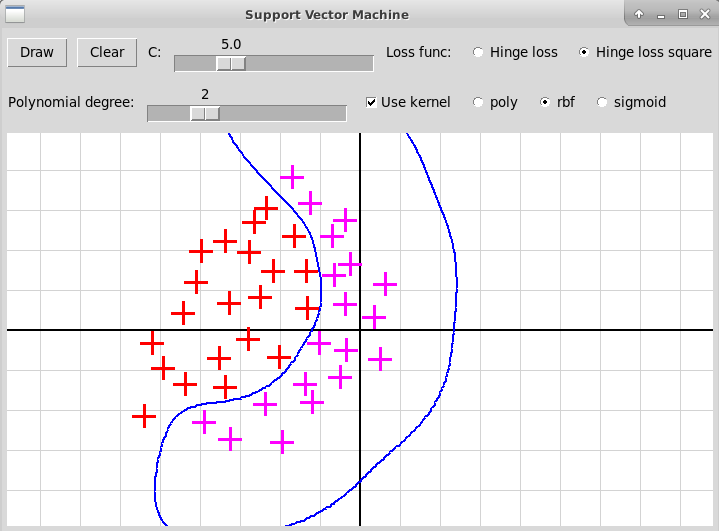
Полиномиальное ядро, степень 2
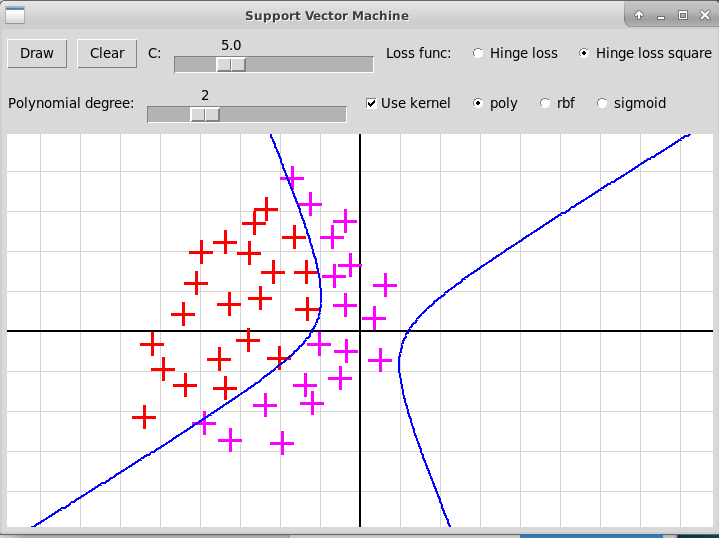
Полиномиальное ядро, степень 3
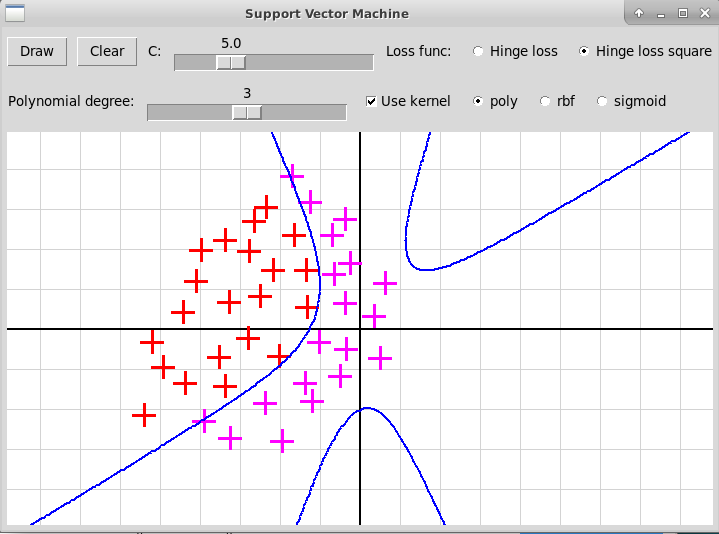
В этой программе используется модуль sklearn и его подмодуль svm, в котором реализован ядровый метод опорных векторов. В программе кликами мыши задается массив точек points, при этом точки, отмеченные кликом левой клавиши мыши, относятся к первому классу, другой клавишей — ко второму, номера клавиш мыши содержится в массиве mouseButtons. Вот как выглядит код, вызывающий метод опорных векторов.
Описания и глобальные переменные:
import numpy as np from sklearn.svm import SVC classifier = SVC(kernel="rbf")Обучение классификатора на тренировочной выборке:
global classifier
. . .
if kernel == "rbf":
classifier = SVC(C=c, kernel="rbf")
else:
classifier = SVC(C=c, kernel="poly", degree=polynomialDegree)
data = [
[points[i].x, points[i].y]
for i in range(len(points))
]
data = np.array(data)
y = [
(1. if mouseButtons[i] == 1 else (-1.))
for i in range(len(points))
]
y = np.array(y)
classifier.fit(data, y)
Для определения класса точки p
можно использовать два метода классификатора:1) метод classifier.predict(x) возвращает 1 для первого класса и -1 для второго;
2) метод decision_function(x) возвращает значение, пропорциональное расстоянию со знаком от точки x до разделяющей гиперплоскости. Для более точного рисования линии уровня естественно использовать именно этот метод.
def classifierValue(p):
x = np.array([[p.x, p.y]])
# return classifier.predict(x)
return classifier.decision_function(x)
Используя значения, возвращаемые классификатором для точек плоскости, программа рисует линию нулевого уровня этой функции, заданную уравнением
Пример применения ядрового метода опорных векторов в среде Jupyter-Lab
В среде Jupyter-Lab мы сначала генерируем на плоскости случайные точки двух классов так, чтобы их невозможно было разделить прямой линией. Затем мы применяем ядровый метод опорных векторов с Гауссовским ядром "rbf" (Radial Basis Function) и рисуем линию, которая разделяет два класса. Вот код программы (в среде Jupyter-Lab):
# Kernel Support Vector Machine Method
from scipy.optimize import minimize
import numpy as np
import random
from math import sin, cos
import matplotlib.pyplot as plt
from skimage import measure
from sklearn.svm import SVC
get_ipython().run_line_magic('matplotlib', 'inline')
plt.axes(aspect="equal")
m1 = 100
class1 = [ np.array([
random.normalvariate(1., 1.5), random.normalvariate(1., 0.5)
]) for i in range(m1) ]
m2 = m1
angle1 = -np.pi*2/3
angle2 = np.pi*2/3
ex = np.array([1., 0.]); ey = np.array([0., 1.])
class2 = []
for i in range(m2):
phi = random.normalvariate(0., 1.)
r = random.normalvariate(5., 0.5)
p = ex*cos(phi)*r + ey*sin(phi)*r
class2.append(p.copy())
x = class1 + class2
x = np.array(x)
y = [1.]*len(class1) + [-1.]*len(class2)
y = np.array(y)
m = len(x)
perm = np.random.permutation(m)
x = x[perm]
y = y[perm]
plt.scatter(
[c[0] for c in x], [c[1] for c in x],
color=[ "r" if yy > 0. else "g" for yy in y ]
)
degree = 2
C = 2. # Hyperparameter
# classifier = SVC(C=C, kernel="poly", degree=degree)
classifier = SVC(C=C, kernel="rbf")
classifier.fit(x, y)
def classifierValue(x):
xx = np.array([ [x[0], x[1]] ])
# return classifier.predict(xx)
return classifier.decision_function(xx)
# Draw the separating line
xmin = min([xx[0] for xx in x]) - 1.
xmax = max([xx[0] for xx in x]) + 1.
ymin = min([xx[1] for xx in x]) - 1.
ymax = max([xx[1] for xx in x]) + 1.
steps = 100
def xcoord(j):
dx = (xmax - xmin)/steps
return xmin + j*dx
def ycoord(i):
dy = (ymax - ymin)/steps
return ymin + i*dy
# a is a matrix of dimension (steps, steps)
a = np.array([[0.]*steps for iy in range(steps)])
for i in range(steps):
for j in range(steps):
xx = np.array([xcoord(j), ycoord(i)])
a[i, j] = classifierValue(xx)
nullContours = measure.find_contours(a, 0.)
for c in nullContours:
plt.plot(
[xcoord(cc[1]) for cc in c],
[ycoord(cc[0]) for cc in c],
color="blue"
)
Вот результат работы этой программы (запущенной в среде Jupyter-Lab):
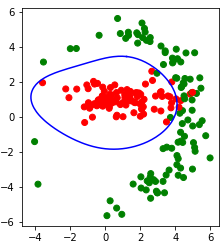
Исходный код программы:
"svmKernel.ipynb".
Домашнее задание
В задании 2 варианта. Студенты с нечетными номерами по журналу
делают вариант 1, с четными — вариант 2. В обоих вариантах
надо изменить оконную программу
"svm.py" (полный архив всех исходных файлов
"svm.zip"), в которой реализован классический
линейный метод опорных векторов:

-
Переделать программу
"svm.py", в которой реализован
линейный метод опорных векторов.
Надо дополнить признаки объектов
всеми мономами (произведениями) степени ≤ d от исходных признаков,
число d должно задаваться слайдером. Например, при d=2 мы
вместо точки
x = (x0, x1) ∈ R2используем "расширенную" точкуx' = (1, x0, x1, x02, x0x1, x12) ∈ R6,при d=3 получится 10-мерное пространство и т.д. Линейный классификатор вычисляется для расширенного пространства. Программа должна нарисовать линию, разделяющую точки двух классов.
-
Переделать программу "svm.py",
в которой реализован классический
линейный метод опорных векторов. Модифицированная программа
должна использовать ядровый метод опорных векторов, реализованный
в стандартных модулях Питона в виде класса SVC:
from sklearn.svm import SVC
Программа должна применить классификатор SVC и нарисовать линию, разделяющую точки двух классов. В программе должна быть реализована возможность выбора ядра из двух вариантов: "rbf" (Гауссовское ядро), "poly" (полиномиальное ядро). В случае полиномиального ядра степень полинома должна задаваться с помощью слайдера.
1.6. Синтаксический разбор. Реализация сканера с помощью регулярных выражений, рекурсивная реализация парсера
-
Проект "Компилятор формул"
lparser.py:
компилятор формул в обратную польскую запись и стековый вычислитель, реализованный в виде класса Parser. Для лексического анализа используется модуль re (сокращение от regular expressions), реализующий работу с регулярными выражениями. Синтаксический анилиз использует алгоритм рекурсивного разбора LL(1). -
Проект "Рисование графика функции, заданной в текстовом окне":
plotFunction.zip
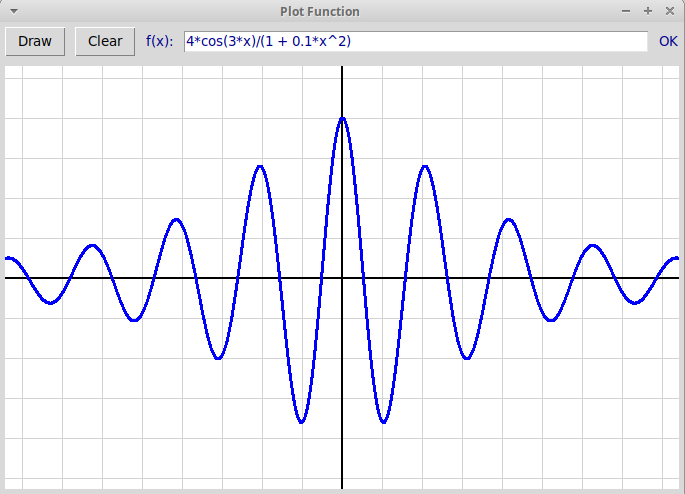
Архив plotFunction.zip содержит файлы:- "lparser.py" компилятор формул в обратную польскую запись и стековый вычислитель, (class Parser);
- "plotFunction.py" графическая программа, рисующая график функции, которая вычисляется по ее текстовой записи с помощью компилятора формул;
- "R2Graph.py" модуль R2Graph, реализующий классы вектор R2Vector и точка R2Point на плоскости, который используются в любых геометрических и графических задачах.
Из программы прошлого года
1.6. Параллельное программирование на языке Python: нити и объекты синхронизации
Презентация: Нити и объекты синхронизации
Примеры программ
-
Простейший пример на использование нитей и мьютекса —
жеребьевка: headsTails.py.
Программа использует модуль threading.
Запускаются две однотипные нити (объект Thread), первая 10 раз печатает слово "Heads", вторая "Tails", в промежутках между печатями каждая нить засыпает на случайное время в интервале от 0.1 до 1 секунды. Выигрывает та нить, которая напечатает свое слово последней. Для предотвращения каши на печати нити для доступа к консоли используют мьютех (в языке Python он называется Lock), захват мьютекса производится методом acquire(), освобождение — release(). Ожидание завершения нити выполняется с помощью метода join() объекта типа Thread.
Задачи
- Вычислить определенный интеграл от заданной функции, разбив отрезок интегрирования на n частей (n небольшое!) и запустив для каждой части отдельную нить.
- Перемножить две квадратные n*n-матрицы, запустив k*k нитей, где k делит n. Нить с индексами (s,t) вычисляет минор матрицы-произведения в строках s*m+1, ..., s*m+m и столбцах t*m+1, ..., t*m+m, где m = n/k. (Результирующая матрица разбивается на клетки размера m = n/k, каждая нить вычисляет одну клетку.)
- Привести матрицу к ступенчатому виду методом Гаусса, используя параллельную работу со строками матрицы при обнулении очередного столбца.
1.7. Сетевые приложения на языке Python, интерфейс сокетов
Примеры программ
- Скачать страницу из Internet по протоколу HTTP: httpGet.py
- Пара простейших программ, использующих протокол UDP и групповое широковещание (multicast): программа udpSnd.py раз в секунду посылает дейтаграму по широковещательному адресу (224.1.1.22, 1234), которая содержит текущее время в текстовом формате. Программа udpRecv.py принимает эти дейтаграмы и распечатывает их на консоли.
Тема 2. Система компьютерной математики SageMath
2.1. Задачи по геометрии
Решения всех задач должны быть оформлены как функции на языке Sage (аналогичны функциям в языке Python). Например, в задаче "Нарисовать треугольник, вписанную окружность и точку Жергона" решение оформляется в виде функции, на вход которой подаются 3 точки и которая возвращает графический объект.
Пример решения задачи:
нарисовать треугольник, вписанную и описанную вокруг него окружности,
а также изобразить процесс их построения —
биссектрисы и серединные перпендикуляры.
Код sage-программы: "geometry.sage".
Пример использования функции:
sage: load("geometry.sage")
sage: a = vector([0, 0])
sage: b = vector([5, 1])
sage: c = vector([3, 5])
sage: drawTriangle(a, b, c)
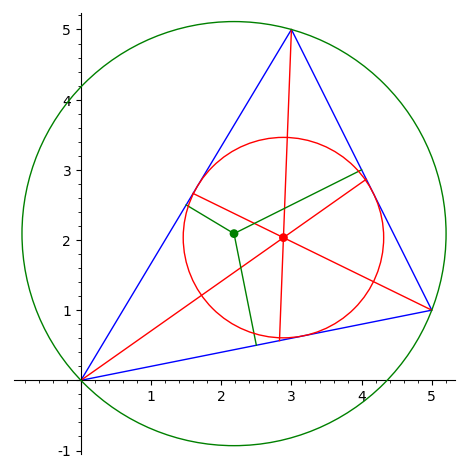
Список задач
-
Нарисовать треугольник, вписанную окружность и точку Жергона.

-
Нарисовать треугольник, три внешне вписанных окружности и точку Нагеля.

-
Нарисовать треугольник и точку Лемуана, которая построена как
точка, изогонально сопряженная к точке пересечения медиан.

-
Нарисовать треугольник и точку Ферма-Торичелли (точка, минимизирующая
сумму расстояний до вершин треугольника), изобразив процесс ее
построения.

2.2. Кубическая интерполяция и построение кубических сплайнов
Рассматривается задача интерполяции, т.е. построения функции y = f(x) по заданным значениям в дискретном множестве узлов. Чаще всего такая функция строится как сплайн, состоящий из кубических многочленов, причем различаются C1-сплайны с непрерывной первой производной и C2-сплайны, у которых непрерывны первая и вторая производные.
Построение кубического C1-сплайна основано на следующем утверждении.
На следующем рисунке представлен график такого многочлена для значений
Можно самостоятельно вывести формулы для коэффициентов этого многочлена — например, выписав систему из 4-х уравнений и решив ее, либо каким-нибудь другим, более умным способом. Но в любом случае выражения получатся громоздкими, так что лучше предоставить эти вычисления SageMath. Сначала зададим переменные x0, x1, p0, p1, dp0, dp1, а также коэффициенты многочлена по возрастанию степеней a0, a1, a2, a3:
var("x0 x1 p0 p1 dp0 dp1")
var("a0 a1 a2 a3")
Зададим многочлен и его производную по x:
p(x) = a0 + a1*x + a2*x^2 + a3*x^3
dp(x) = derivative(p(x), x)
Выпишем 4 уравнения:
eq0 = (p(x = x0) == p0)
eq1 = (p(x = x1) == p1)
eq2 = (dp(x = x0) == dp0)
eq3 = (dp(x = x1) == dp1)
И теперь решим систему уравнений относительно неизвестных a0, a1, a2, a3, воспользовавшись функцией solve:
res = solve([eq0, eq1, eq2, eq3], [a0, a1, a2, a3])
Результатом является список решений, в данном случае состоящий из одного элемента (т.е. решение единственно). Решение — это список из 4-х уравнений, каждое из них имеет вид
sage: res[0][0]
a0 == -((dp1*x1 - p1)*x0^3 + p0*x1^3 + ((dp0 - dp1)*x1^2 + 3*p1*x1)*x0^2 -
(dp0*x1^3 + 3*p0*x1^2)*x0)/(x0^3 - 3*x0^2*x1 + 3*x0*x1^2 - x1^3)
Если нам нужно выражение для свободного члена, а не уравнение,
то можно воспользоваться методом rhs(), который возвращает
правую часть уравнения (от слов right hand side):
sage: res[0][0].rhs()
-((dp1*x1 - p1)*x0^3 + p0*x1^3 + ((dp0 - dp1)*x1^2 + 3*p1*x1)*x0^2 -
(dp0*x1^3 + 3*p0*x1^2)*x0)/(x0^3 - 3*x0^2*x1 + 3*x0*x1^2 - x1^3)
Получив выражения для коэффициентов многочлена интерполяции,
нетрудно нарисовать его график. Соответствующая программа
содержится в файле
"cubicPol.sage". Вот
пример ее выполнения:
sage: load("cubicPol.sage")
sage: drawCubicInterpolation(xx0=-5, xx1=6, y0=-4, y1=1, dy0=3, dy1=1)
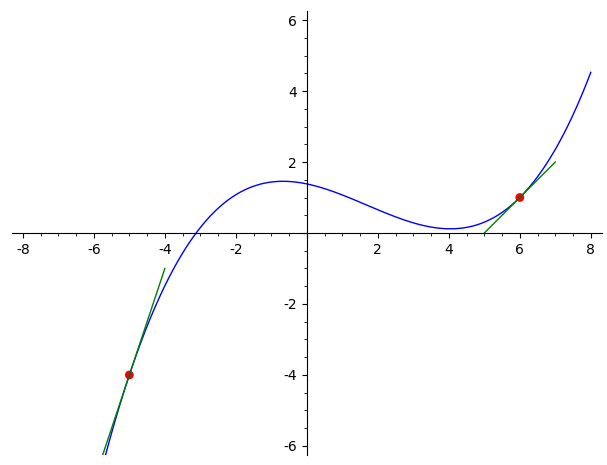
Задачи на построение кубического сплайна
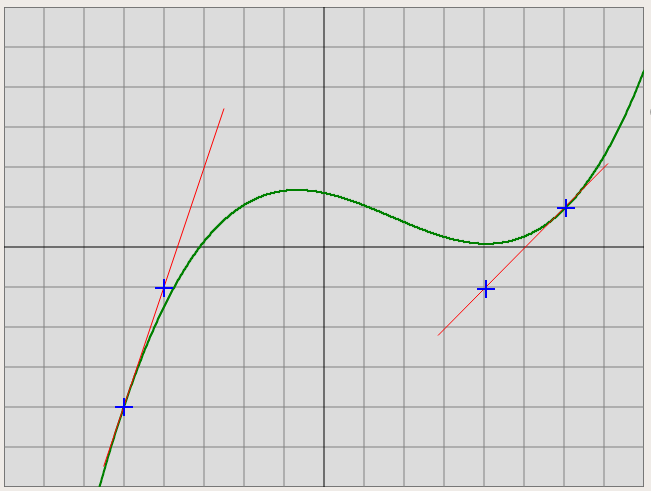
В задачах надо написать функцию (в смысле Python'а) с именем splineC1 или splineC2, на вход которой передается список пар. Каждая пара содержит координаты (xi, yi) i-го узла интерполяции, при этом координаты x идут в строго возрастающем порядке. Функция должна построить кубический C1 или С2-сплайн (с непрерывными только первыми производными или как первыми, так и вторыми производными). Пример использования функции:
s = splineC1([(-7,-4), (-5,-1), (-3,-2), (-1,2),
(1,3), (3,1), (5,3), (7,-1)])
show(s, aspect_ratio=1)
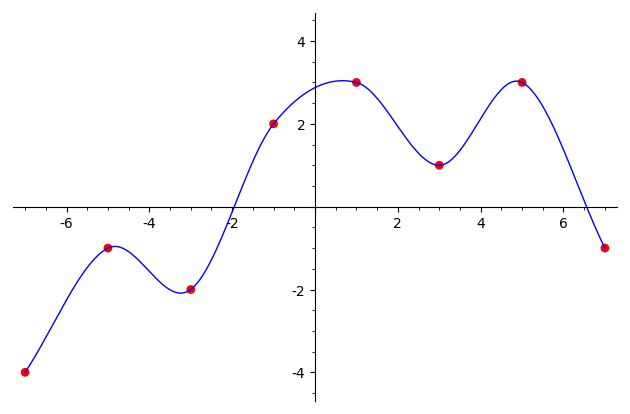
При построении C1-сплайна надо дополнительно задать производные в каждом узле, они определяются как полусумма значений тангенсов наклона звеньев ломаной слева и справа от узла. В начальном и конечном узлах производная задается как тангенс угла наклона звена ломаной, выходящего из этого узла.
При построении C2-сплайна решается система линейных уравнений, где неизвестными являются коэффициенты кубических многочленов, составляющих сегменты сплайна. Пусть дан n+1 узел:
2) правый сегмент сплайна принимает значение yi,
3) производные левого и правого сегментов сплайна равны между собой,
4) вторые производные левого и правого сегментов сплайна равны между собой.
2) значение второй производной начального сегмента сплайна в точке x0 равно нулю,
Файл "splineC2_3Nodes.sage" содержит решение этой задачи для случая трех узлов. Вот пример работы программы:
sage: load ("splineC2_3Nodes.sage")
sage: splineC2([(-1, -1), (0, 1), (2, 0)])
Matrix of the system:
[ 1 -1 1 -1 0 0 0 0]
[ 0 0 2 -6 0 0 0 0]
[ 1 0 0 0 0 0 0 0]
[ 0 0 0 0 1 0 0 0]
[ 0 1 0 0 0 -1 0 0]
[ 0 0 2 0 0 0 -2 0]
[ 0 0 0 0 1 2 4 8]
[ 0 0 0 0 0 0 2 12]
Column of free terms: (-1, 0, 1, 1, 0, 0, 0, 0)
Solution of the system: (1, 7/6, -5/4, -5/12, 1, 7/6, -5/4, 5/24)
Resulting spline: [(1, 7/6, -5/4, -5/12), (1, 7/6, -5/4, 5/24)]
Launched png viewer for Graphics object consisting of 5 graphics primitives
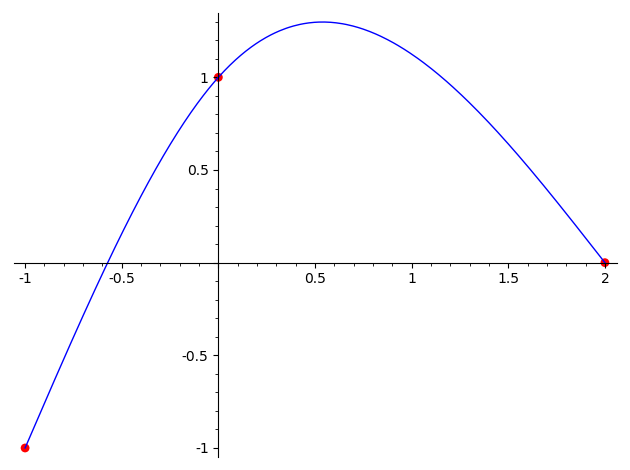
Список задач
Студенты с нечетными номерами по журналу делают первую задачу, с четными — вторую.
-
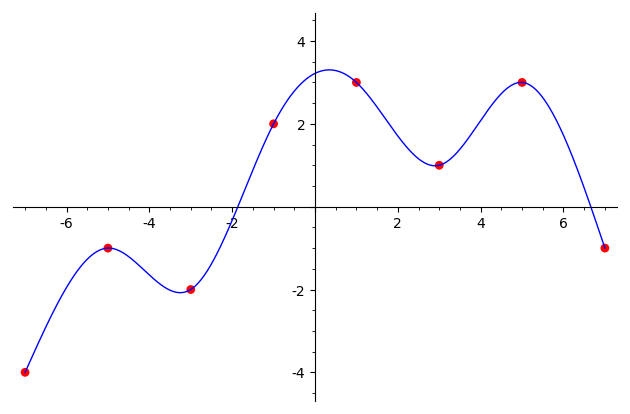
Построить C1-сплайн.

-
Построить C2-сплайн.
2.3. Коммутативная алгебра: системы алгебраических уравнений и базисы Гребнера
Рассматриваются кольца многочленов от нескольких переменных над полем комплексных чисел, конечные наборы многочленов в них, порождаемые ими идеалы и аффинные многообразия. Предполагаются известными теоремы Гильберта о конечности базисов и о нулях, а также теория базисов Гребнера. Рекомендуется книга
а также пособие по математическому практикуму для группы алгебры Презентация к лекции по коммутативной алгебре
Пример решения задачи: определить принадлежность многочлена от многих переменных к радикалу идеала I
Рассматривается алгебра многочленов от нескольких переменных над полем комплексных чисел. В SageMath кольцо многочленов задается предложением
R = PolynomialRing(CC, "x, y, z", order="lex")
Здесь СС — поле комплексных чисел,
"x, y, z" — названия
трех переменных; параметр order="lex" задает чисто лексикографический
порядок на мономах. Многочлены (т.е. элементы кольца R),
соответствующие переменным x, y, z, можно задать
с помощью следующих предложений:
x = R.gen(0); y = R.gen(1); z = R.gen(2)
или в одной команде (учитывая особенности языка Python):
x, y, z = R.gens()
Можно также задать многочлены-образующие кольца непосредственно в
предложении, определяющем кольцо:
R.<x0, x1, x2> = PolynomialRing(CC, 3, "x", ordel="lex")
Здесь определено кольцо многочленов над полем комплексных чисел от 3-х
переменных, префикс названия переменных "x".
Радикалом идеала I называется множество многочленов, степени которых лежат в идеале I:
Реализуем в SageMath функцию, проверяющую, лежит ли многочлен f в радикале идеала I, заданного многочленами из списка s:
def inRadical(f, s):
sum = f
for g in s:
sum += g
R = parent(sum)
variables = [ str(v) for v in R.gens() ]
variables.append("yyy")
H = PolynomialRing(CC, variables)
yyy = H.gens()[-1]
s1 = s.copy()
s1.append(1 - yyy*f)
J = ideal(s1).groebner_basis()
return J == [1.]
Программа записана в файле "radical.sage".
Пример применения этой функции:
sage: load("radical.sage")
sage: R. = PolynomialRing(CC, "x, y, z")
sage: g = (x^2 + y^2 - 1)^2
sage: h = x^2 + y^2 + z^2 + 1
sage: f = z^2 + 2
sage: f in ideal(g, h)
False
sage: f^2 in ideal(g, h)
True
sage: inRadical(f, [g, h])
True
sage: inRadical(f + 1, [g, h])
False
Домашнее задание
Требуется решить одну задачу из списка: номер 1 для студентов с нечетным номером по журналу, номер 2 с четным. Надо реализовать функцию на языке Sage, которая возвращает значение True или False. Набор многочленов передается функции как список.
Список задач
- Даны два конечных набора многочленов. Определить, задают ли они одно и то же аффинное многообразие.
- Выяснить, имеет ли система алгебраических уравнений лишь конечное число решений (при этом хотя бы одно решение должно существовать).
Весенний семестр прошлого года (весна 2020)
Журнал группы магистратуры 1 курса, 2019-20 уч. год.Видео лекций (весна 2020)
-
Графика на языке Python: захват и перемещение элементов картинки
мышью.
Введение в SageMath (начало). Видео первой части лекции. -
Введение в систему компьютерной математики SageMath.
Видео второй части лекции.
Лекция 25 марта 2020: Нити и объекты синхронизации
Лекция 1 апреля 2020: не состоится ввиду объявленных каникул до 5 апреля.
Лекция 8 апреля 2020: Графика на языке Python
Лекция 15 апреля 2020:
Лекция 22 апреля 2020: SageMath, построение кубического сплайна.
Видео.
Лекция 6 мая 2020: Базисы Грёбнера в кольцах многочленов
от нескольких переменных.
Видео,
презентация.
Семинар 13 мая 2020: решения задач на базисы Грёбнера в
кольцах многочленов, сплайны и др.
Видео.