Магистратура мехмата:
цифровые технологии и искусственный интеллект
Компьютерный практикум, семинары
В весеннем семестре 2022-23 уч.г. занятия проходят дистанционно
с использованием MS Teams на факультете.
Время встречи (Meeting):
пятнца в 16:45 (потенциально до 20:00).
При проблемах с MS Teams можно использовать Zoom.
Ссылка на конференцию:
https://us05web.zoom.us/j/2842740990?pwd=bkhtRlNxL3E3SnZCTU1oSFNHcHJNQT09
Passcode: 1
Самостоятельная работа состоит в решении задач по темам,
которые обсуждаются в лекциях.
По каждой теме нужно решить одну задачу из предлагаемого списка.
Номер задачи равен номеру студента в журнале по модулю n,
где n — число задач по данной теме.
Решения задач присылайте мне на электронную почту в виде одного или
нескольких файлов, присоединенных к письму (если файлов много,
то лучше присылать zip-архив с файлами в поддиректории).
Адрес моей электронной почты:
vladibor266 (собака) gmail.com
Тема письма должна начинаться со слов "Магистратура ИИ".
Содержание
2022-23 учебный год
-
Весенний семестр 2023
Записи лекций на "виртуальной доске" (весенний семестр)- Семинар 10.02.2023: метод наименьших квадратов
- Семинар 17.02.2023: градиентный спуск и его ускоренные варианты
- Семинар 3.03.2023: стохастический градиентный спуск
- Семинар 10.03.2023: классический (линейный) метод опорных векторов
- Семинар 17.03.2023: нелинейный метод опорных векторов
-
Семинар 24.03.2023:
ядровый метод опорных векторов.
Классификация рукописных цифр с помощью (ядрового) метода опорных векторов. - Семинар 31.03.2023: Борьба с выбросами: использование функции потерь Хубера в задаче линейной регрессии. Применение методов линейного программирования при минимизации абсолютной величины ошибки (функция MAE — Mean Absolute Error).
- Семинар 7.04.2023: Метод главных компонент. Классификация рукописных цифр с помощью (ядрового) метода опорных векторов, на вход которому подаются только главные компоненты объектов.
-
Семинар 14.04.2023.
Байесовские классификаторы:
1) наивный байесовский классификатор GaussianNB —
в каждом классе
нормальное распределение объектов, причем координаты не зависят
друг от друга (матрица ковариаций диагональная);
2) линейный классификатор LinearDiscriminantAnalysis — у каждого класса нормальное распределение, причем матрицы ковариаций для всех классов одинаковы;
3) квадратичный классификатор QadraticDiscriminantAnalysis наиболее общий. Единственное ограничение — точки одного класса распределены по нормальному закону, параметры распределений могут быть разными для разных классов. -
Семинар 21.04.2023.
Кластеризация (обучение без учителя).
Есть набор объектов без разметки. Мы хотим разбить их на классы (метод fit), а также построить классификатор, который для любой точки предсказывает номер класса, к которому ее следует отнести (метод predict). Мы рассмотрим самые простые и популярные методы кластеризации K-Means и DBSCAN. Рассматривается метод K средних (K-Means). -
Семинар 28.04.2023.
Рассматривается наиболее популярный метод
кластеризации DBSCAN
(Density-Based Spatial Clustering of Applications with Noise).
Он основан на рассмотрении плотности точек в пространстве и
определении основных точек (core poins), таких, что в их
окрестности радиуса ε содержится не менее minPts
точек; числа ε и minPts являются параметрами алгоритма.
Две точки t1, t2 связны, если
между ними найдется цепочка основных точек
p1, p2, ...,
pn такая, что
точка t1 принадлежит ε-окрестности точки
p1,
точка t2 принадлежит ε-окрестности точки
pn, и для любого
i=1, 2, ..., n-1
точка pi+1
принадлежит ε-окрестности точки
pi.
Каждый кластер состоит
из попарно связных точек. Исходное множество точек
может содержать также выбросы (noise, outliers), которые
не относятся ни к одному из кластеров.
В отличие от метода кластеризации K-Means, в методе DBSCAN не требуется апиори задавать число кластеров; кластеры определяются автоматически на основании параметров ε и minPts (по умолчанию ε=0.5, minPts=5).
-
Семинар 05.05.2023.
Решающие деревья (Decision Trees) используются в задачах
классификации или регрессии (обучение с учителем).
Имеем размеченное множество объектов
X⊂Rn,
X = {x1, x2,
..., xm}.
В задаче классификации разметка — это массив
номеров классов
y = {y1, y2,
..., ym}, где
yi∈Z —
номер класса объекта xi.
В задаче регрессии разметка — это массив
вещественных чисел yi∈R,
представляющих собой значения зависимой величины
y=y(x) на объектах
xi.
Классификатор представляет собой бинарное дерево, в каждой вершине которого задан предикат Q(j, t), где j — номер координаты объекта, t — пороговое значение. На объекте x предикат принимает значение 1 (True), если j-я координата xj объекта x не превосходит порогового значения t, и 0 (False) в противном случае:
Q(j, t)(x) = (xj ≤ t)Каждой внутренней (не терминальной) вершине дерева соответствует некоторое подмножество S⊂X тренировочного множества X объектов, корню дерева соответствует все множество X. Предикат в этой вершине разделяет подмножество S на две части, соответствующие ее левой и правой дочерним вершинам:Sleft = { x∈S: xj≤t }, Sright = { x∈S: xj>t }.В терминальных вершинах (листьях) дерева предикаты уже не заданы, а подмножество объектов, соответствующее терминальной вершине, содержит в случае задачи классификации уже объекты почти все одного класса, за возможным исключением незначительного числа объектов; терминальная вершина задает этот номер класса. В случае задачи регрессии значения объектов, относящихся к терминальной вершине, близки друг другу, а вершина задает среднее значение этих объектов.Программа "decisionTrees.py" (архив "decisionTrees.zip") иллюстрирует графически построение решающего дерева и основанного на нем классификатора. Точки, соответствующие двумерным объектам, можно ставить кликами трех клавиш мыши (они задают 3 класса) или генерировать случайным образом:
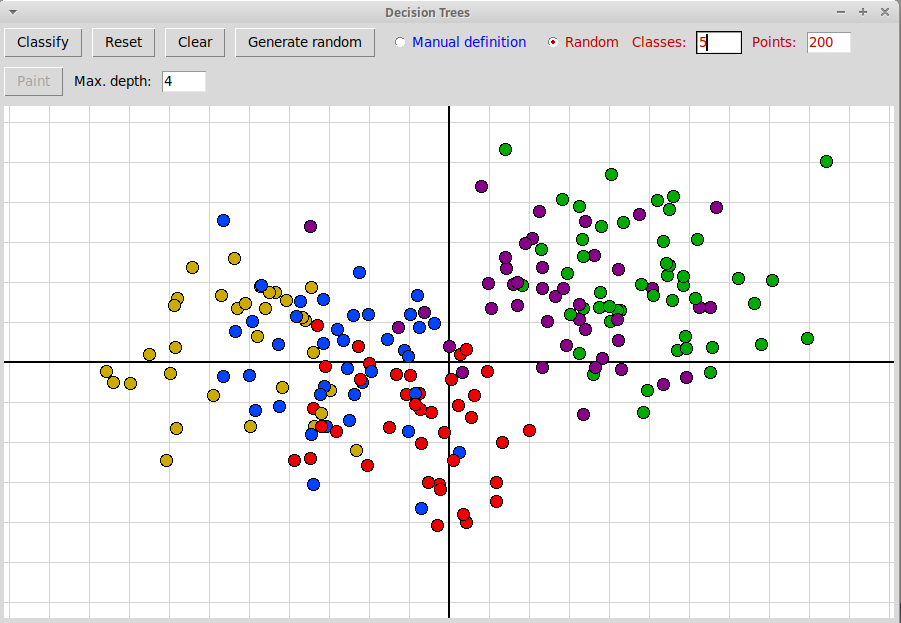
По нажатию на клавишу "Classify" создается классификатор, основанный на решающем дереве, и с его помощью тренировочные объекты классифицируются. Те объекты, класс разметки которых совпадает с результатом классификации, изображаются квадратиками, те, классификация которых не совпадает с разметкой, изображаются кружочками:
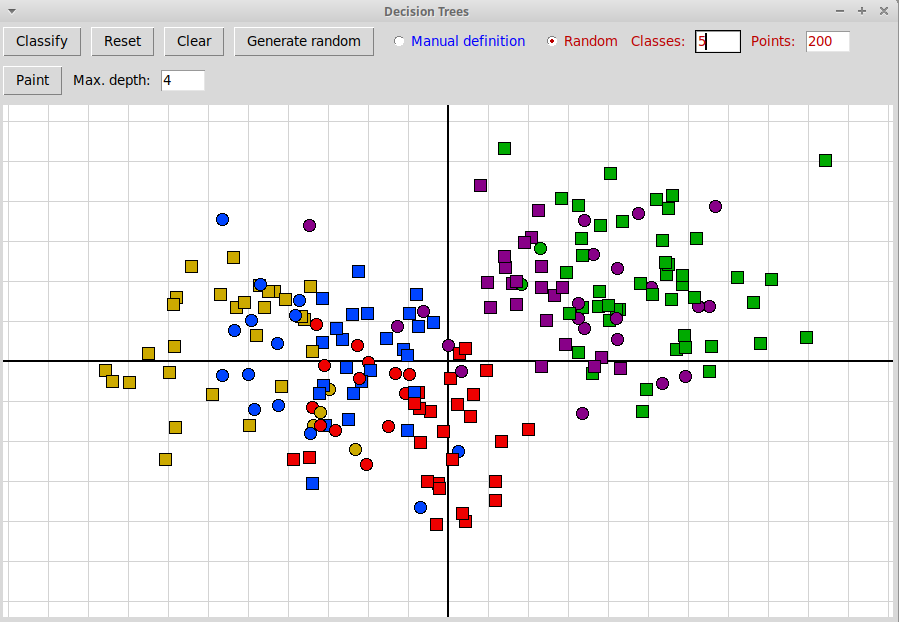
По нажатию на клавишу "Paint" классификатор применяется ко всем точкам плоскости:
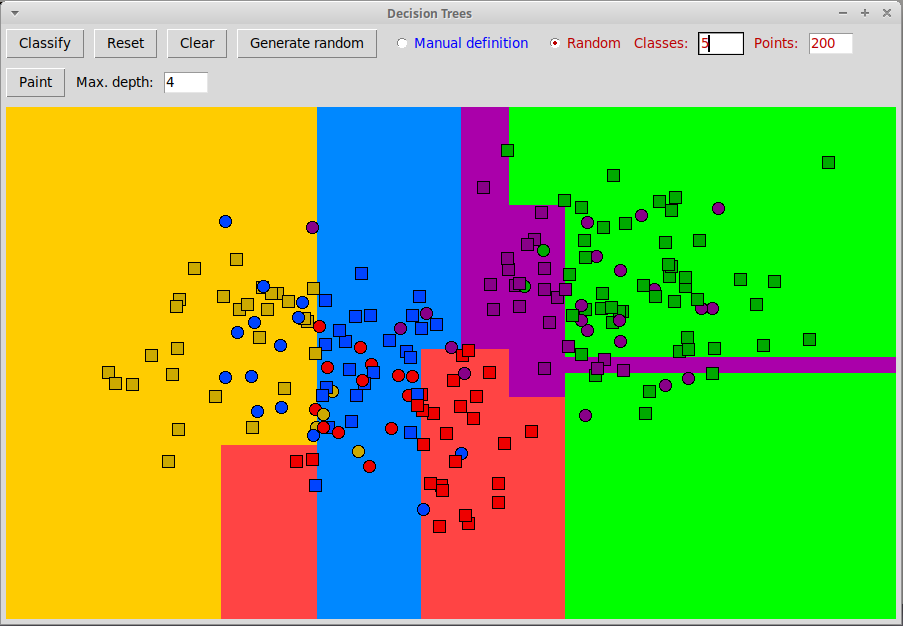
Эта картинка показывает, что все пространство разбивается на n-мерные ящики (в случае плоскости — прямоугольники), поскольку в вершинах используются простейшие предикаты, в которых только одна координата объекта сравнивается с пороговым значением. -
Семинар 12.05.2023.
Решающие деревья (Decision Trees), продолжение.
Объяснение критерия Джини (impurity) в задаче классификации.
Применение решающих деревьев в задаче регрессии:
представление изображения в виде кусочно-постоянной функции
с помощью решающего дерева, реализация такой программы на
Питоне с использованием модулей tkinter и PIL:
"imageRegrTrees.py".
Изображение состоит из трех компонент (красной, зеленой, синей),
каждую компоненту можно представлять как функцию от двух
переменных. Более точно, пиксели каждой из трех компонент
изображения мы представляем как двумерные объекты с
двумя признаками (x0, x1)
— координатами пикселя,
а значение y на каждом объекте — это яркость
пикселя (она изменяется от 0 до 255).
Применив построение трех решающих деревьев
в задаче регрессии для каждой из компонент, мы получим
представление изображения в виде функции на плоскости,
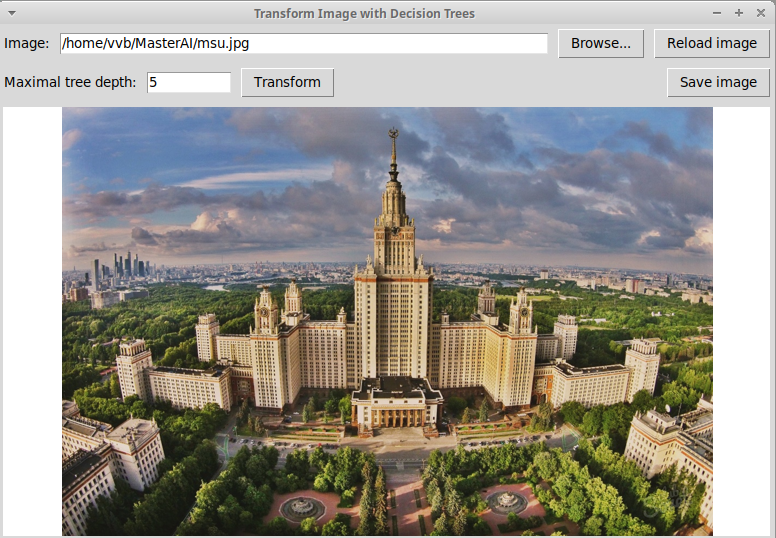
постоянной внутри прямоугольных областей. Ниже приведено
исходное изображение здания МГУ и его представление с
помощью решающих деревьев глубины 10, 15, 20. Изображение
для дерева глубины 20 уже мало отличается от исходного.
Исходное изображение:
 Изображение, построенное с помощью трех решающих деревьев
глубины 10:
Изображение, построенное с помощью трех решающих деревьев
глубины 10:
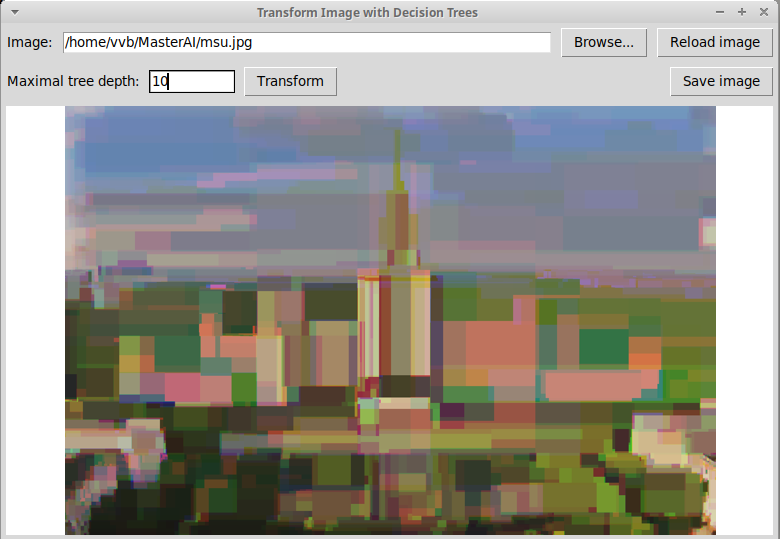
Глубина деревьев 15:
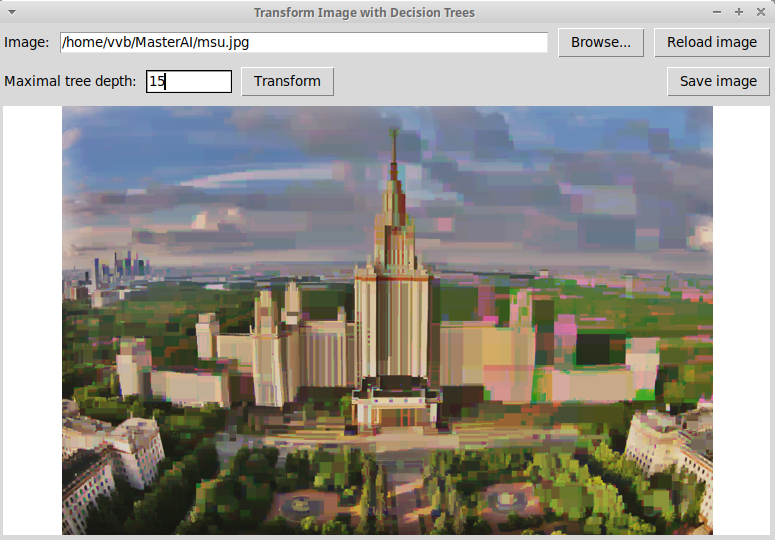
Глубина деревьев 20:
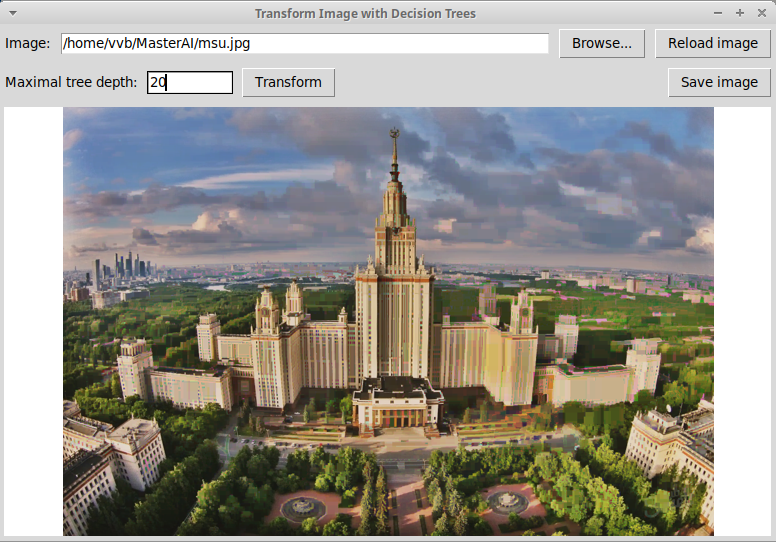
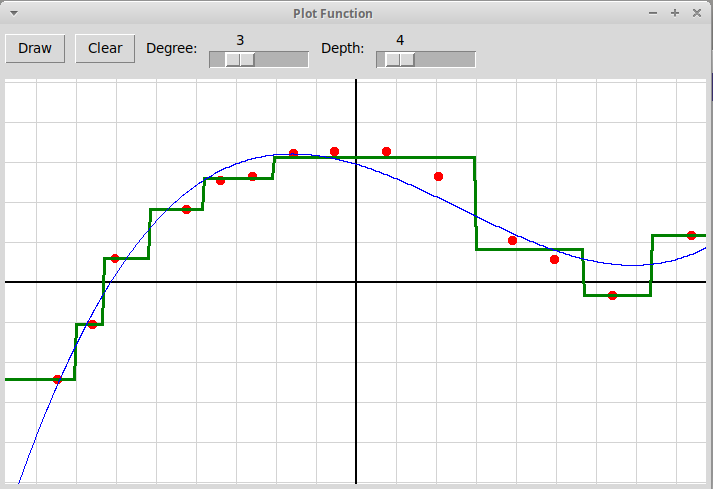
Также применение решающих деревьев в задаче регрессии иллюстрируется программой "regressionTrees.py" (архив всех необходимых файлов "regressionTrees.zip"). В программе по узлам, отмеченным кликами мыши, с помощью решающего дерева заданной глубины строится кусочно-постоянная функция одномерного аргумента
y = f(x), x, y ∈ R,она изображается зеленым цветом. График многочлена заданной степени, построенного по тем же узлам методом наименьших квадратов, изображается синим цветом:
Журнал группы, весенний семестр 2023
-
Домашние задания (весенний семестр)
-
Задача 1
Написать, используя модуль tkinter, оконное графическое приложение, иллюстрирующее метод наименьших квадратов. Пользователь отмечает мышью набор точек на плоскости, программа должна найти многочлен заданной степени, минимизирующий сумму квадратов уклонений значений многочлена от значений, заданных узлами интерполяции:
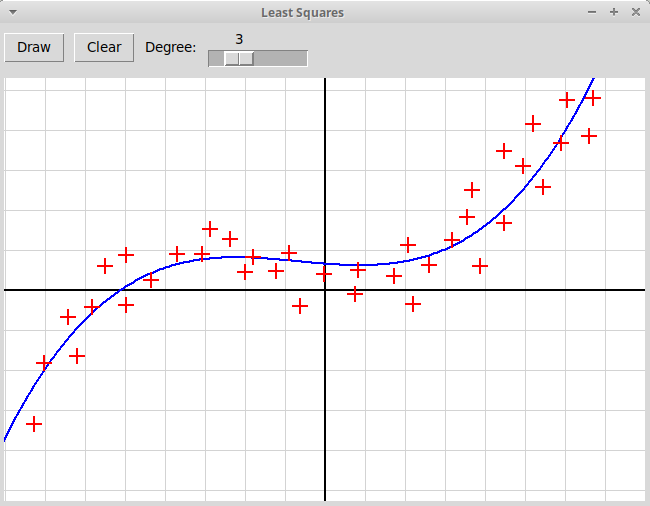
В качестве образца следует использовать программу, рисующую график интерполяционного многочлена по заданным узлам интерполяции; многочлен вычисляется по формуле Ньютона:
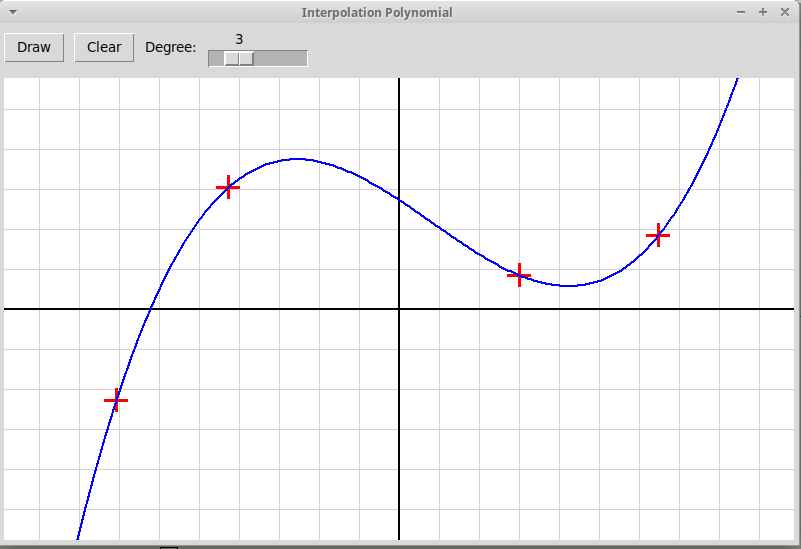
Приложение использует два файла: "newton.py" (оконный интерфейс), "newtonPol.py" (вычисление полинома Ньютона). Архив всех файлов: "newtonInterpol.zip".
-
Задача 2
Дается готовая оконная программа на Python3 + tkinter "gradientDescent.py", иллюстрирующая метод градиентного спуска (программа использует также модули lparser и R2Graph), архив всех файлов: "gradientDescent.zip".
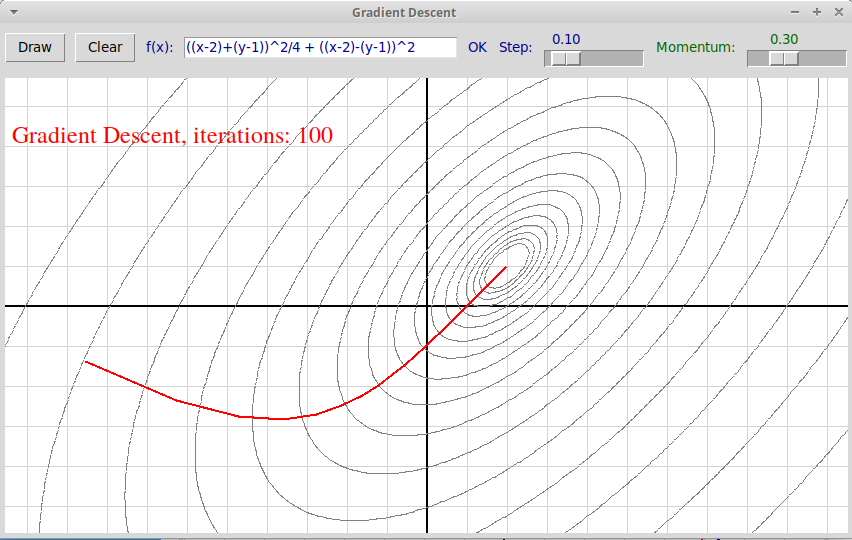
В программе реализован только метод градиентного спуска (запускается по клику левой клавиши мыши), для методов Тяжелого шарика и Ускоренного метода Нестерова оставлены заглушки. Требуется добавить в программу реализацию этих двух методов. Метод Тяжелого шарика запускается по клику средней клавиши мыши (траектория и текст изображаются синим цветом), Ускоренный метод Нестерова запускается по клику правой клавиши мыши (используется зеленый цвет).
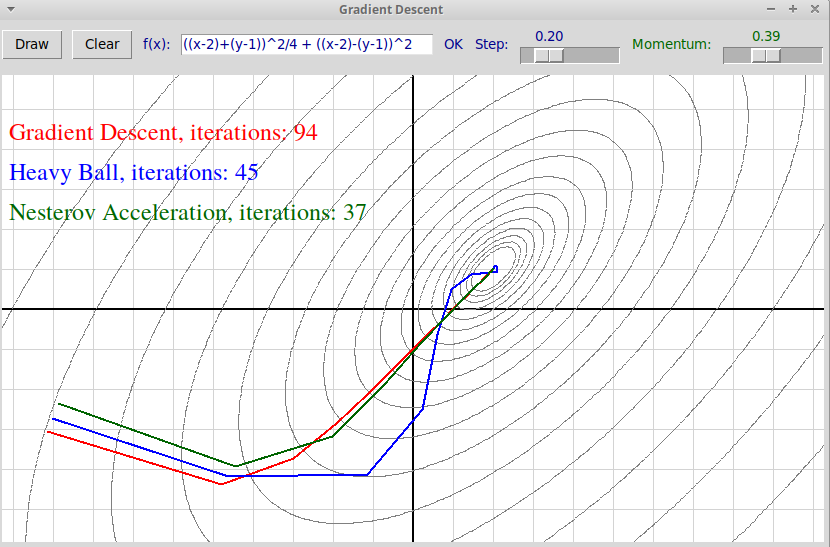
Описание метода градиентного спуска и его ускоренных вариантов
-
Задача 3
Дается готовая оконная программа на Python3 + tkinter "gradientDescent.py", решающая задачу линейной регрессии методом стохастического градиентного спуска. Программа находит многочлен заданной степени, минимизирующий сумму квадратов отклонений от значений в узлах, заданных кликами мыши:
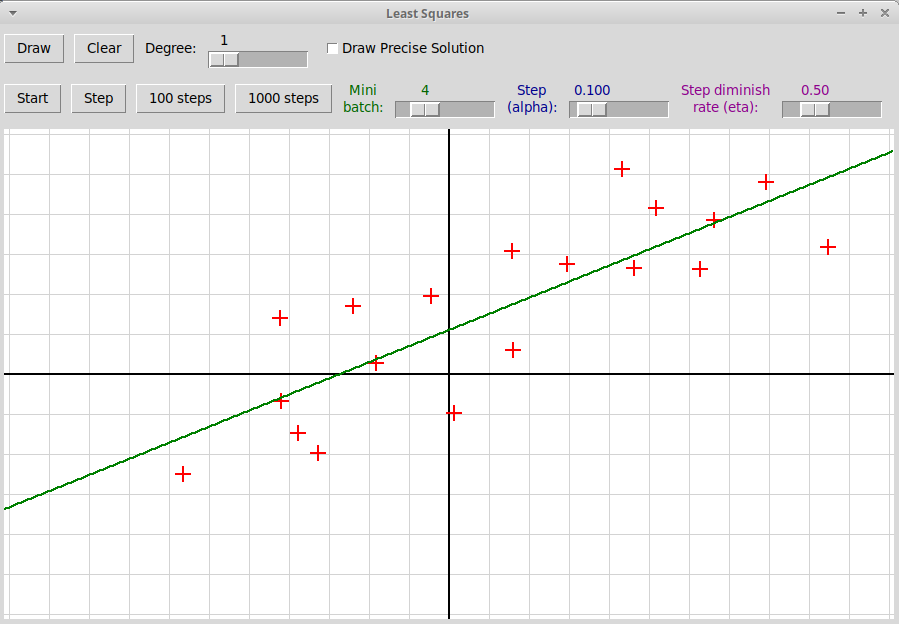
Требуется добавить в эту программу-
регуляризационный член λ||w||2
в функцию потерь L(w) с коэффициентом λ
L(w) = 1/m ∑i (f(xi) - yi)2 + λ||w||2
-
показатель степени β при вычислении размера шага в алгоритме градиентного
спуска:
αi = α0/(1 + η·iβ),где αi — величина i-го шага, α0 — начальная величина шага, константа η — скорость уменьшения шага, β — показатель степени номера шага в знаменателе, 0.5 < β ≤ 1.
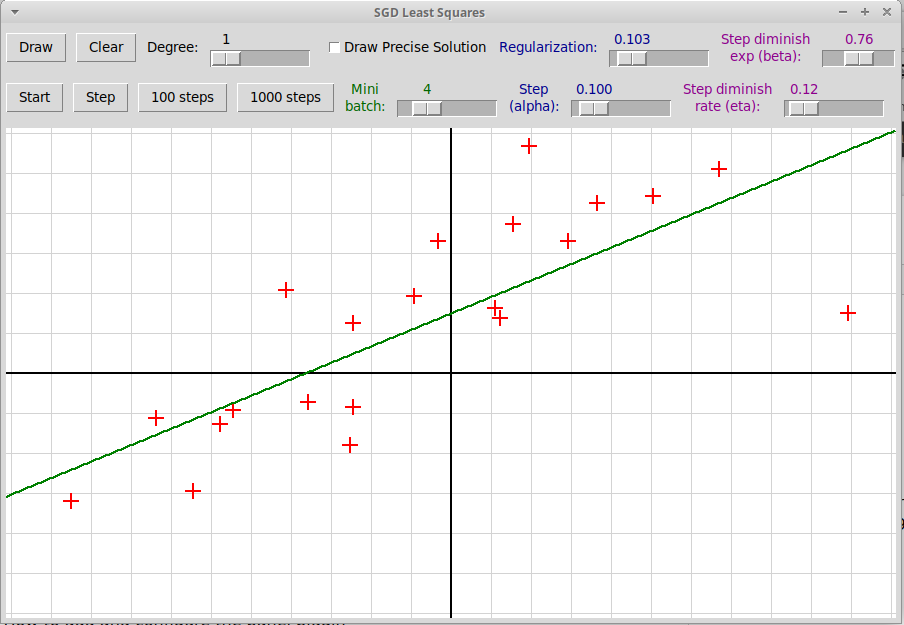
Описание метода стохастического градиентного спуска
-
регуляризационный член λ||w||2
в функцию потерь L(w) с коэффициентом λ
-
Задача 4
Используя ядровый метод опорных векторов, написать программу на Python'е или в jupyter-lab, классифицирующую рукописные цифры из тренировочной базы NIST. Целья является определение оптимальных параметров метода, при которых точность классификации самая высокая.Параметрами является ядро (kernel = "linear", "poly", "rbf"), степень для полиномиального ядра (degree = 2, 3, 4), гиперпараметр C (C = 0.25, 0.5, 1., 2., 4., 8.). Для полиномиального ядра параметр coef0 = 1 (свободный член полинома, вычисляющего ядро, фиксирован и равен 1).
Также следует использовать функцию train_test_split из модуля sklearn.model_selection, которая разбивает исходную (размеченную) базу данных на тренировочную и тестовую части, и функцию accuracy_score из модуля sklearn.metrics, определяющую процент правильных ответов. Классификация выполняется 10 раз (каждый раз база случайно перемешивается) и определяется средняя точность классификации.
Вот примерный текст программы, определяющей точность классификации рукописных цифр методом опорных векторов, использующим Гауссовское ядро "rbf" и гиперпараметр C=1:
import numpy as np from sklearn.datasets import load_digits from sklearn.svm import SVC from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score digits = load_digits() m = len(digits.data) m_train = int(m*3/4) m_test = m - m_train print("Number of digit images:", m) print("Train part:", m_train, " Test part:", m_test) C = 1.0 kernel = "rbf" num_repeats = 10 print("Number of repetitions:", num_repeats) x = digits.data y = digits.target mean_accuracy = 0. for i in range(num_repeats): x_train, x_test, y_train, y_test = train_test_split( x, y, test_size=1/4, shuffle=True, stratify=y ) # model = SVC(C=C, kernel=kernel, degree=degree, coef0=coef0) model = SVC(C=C, kernel=kernel) model.fit(x_train, y_train) y_predicted = model.predict(x_test) accuracy = accuracy_score(y_true=y_test, y_pred=y_predicted) mean_accuracy += accuracy mean_accuracy /= num_repeats print("Mean accuracy of classification:", mean_accuracy)
-
Задача 5
Дополнить программу "huberRegression.py", которая вычисляет линейную регрессию, используя либо метод наименьших квадратов (т.е. минимизируя квадратичную функцию ошибки MSE), либо минимизируя функцию ошибки, определенную с помощью функции Хубера. Архив всех файлов программы: "huberRegression.zip". В программе надо дополнительно реализовать третий способ вычисления параметров регрессии, который минимизирует среднюю величину абсолютной ошибки MAE, используя методы линейного программирования. Модифицированная программа должна выглядеть примерно так:
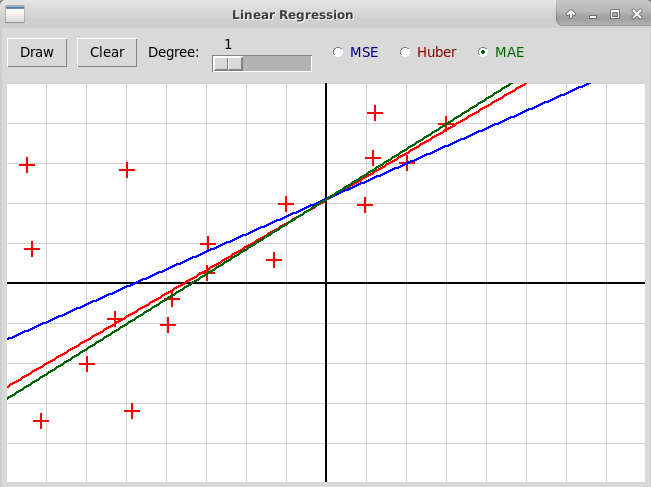
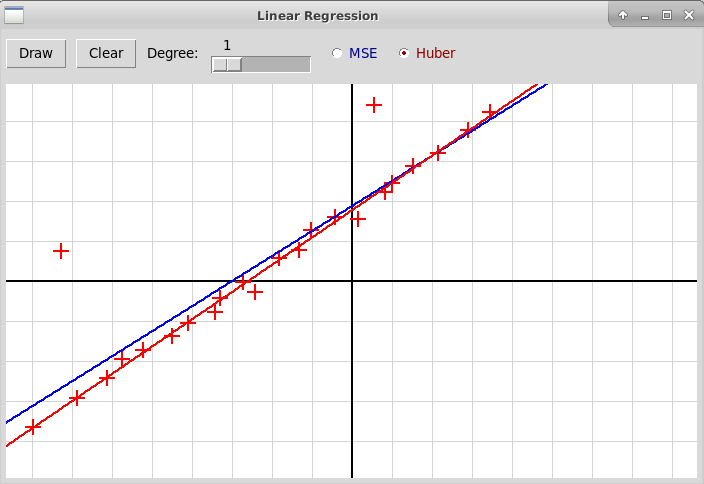
На приведенном скриншоте по заданным узлам строится прямая, т.е. полином степени 1. Синим цветом нарисована прямая, построенная методом наименьших квадратов, красным — с использованием функции Хубера, зеленым — с помощью минимизации функции MAE методом линейного программирования. Можно также построить полином большей степени, например, третьей (степень полинома задается с помощью слайдера):
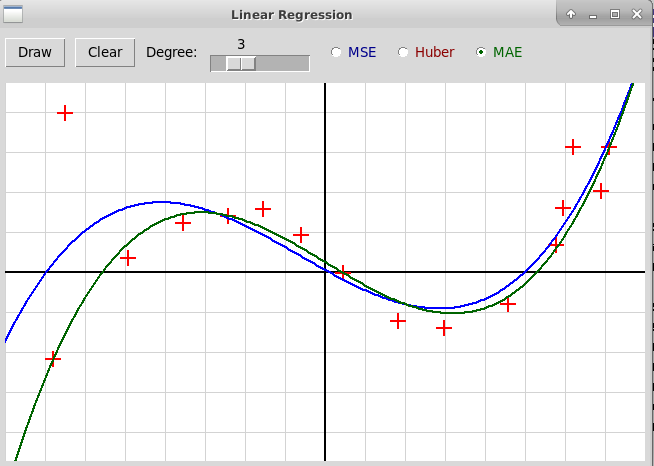
Здесь синяя кривая построена методом наименьших квадратов, зеленая — методом линейного программирования. Видно, что во втором случае влияние выбросов на форму кривой значительно меньше. Красная кривая, построенная с использованием функции Хубера, здесь не показана, потому что она в данном случае почти совпадает с зеленой кривой и на картинке две кривые почти полностью накладываются друг на друга.
-
Задача 6
Применить метод главных компонент при классификации рукописных цифр, которые представляют собой матрицы размера 8x8, т.е. размерность пространства объектов равна 64. Метод главных главных компонент позволяет уменьшить размерность пространста. В задаче надо определить точность классификации цифр ядровым методом опорных векторов при уменьшении числа главных компонент. Нужно построить таблицу, где для каждого числа оставленных главных компонент указывается точность классификации. Число главных компонент должно последовательно принимать значения
1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
15, 20, 30, 40, 50, 60, 64.Пример программы, которая определяет точность классификации для фиксированного числа главных компонент = 8: "digitSvmPcaClassification.py",
-
Задача 7
В программе "clustering.py" (архив "clustering.zip"), иллюстрирующей графически алгоритмы кластеризации, реализовано использование алгоритма K-Means (K средних):
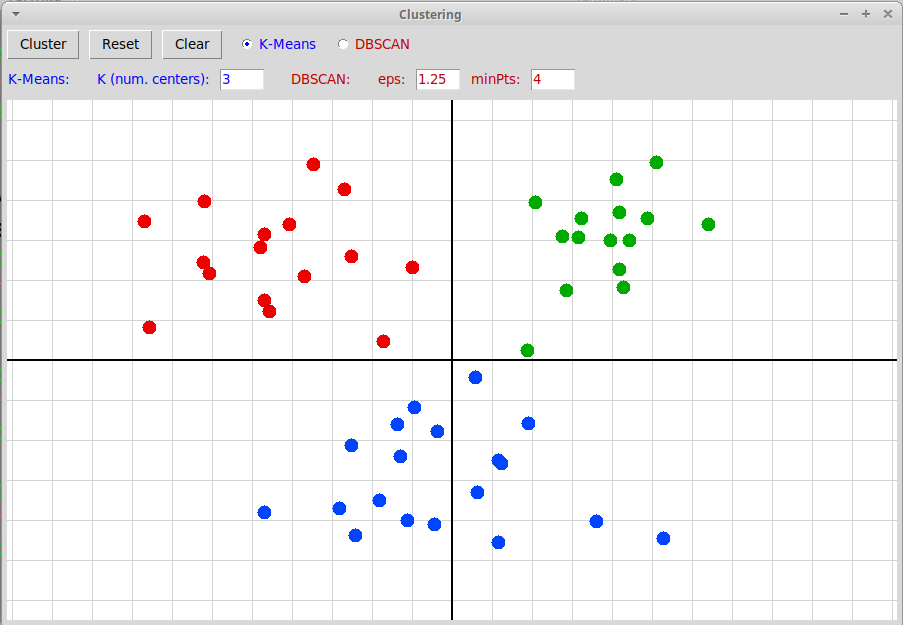
Иллюстрация алгоритма DBSCAN оставлена в качестве упражнения:
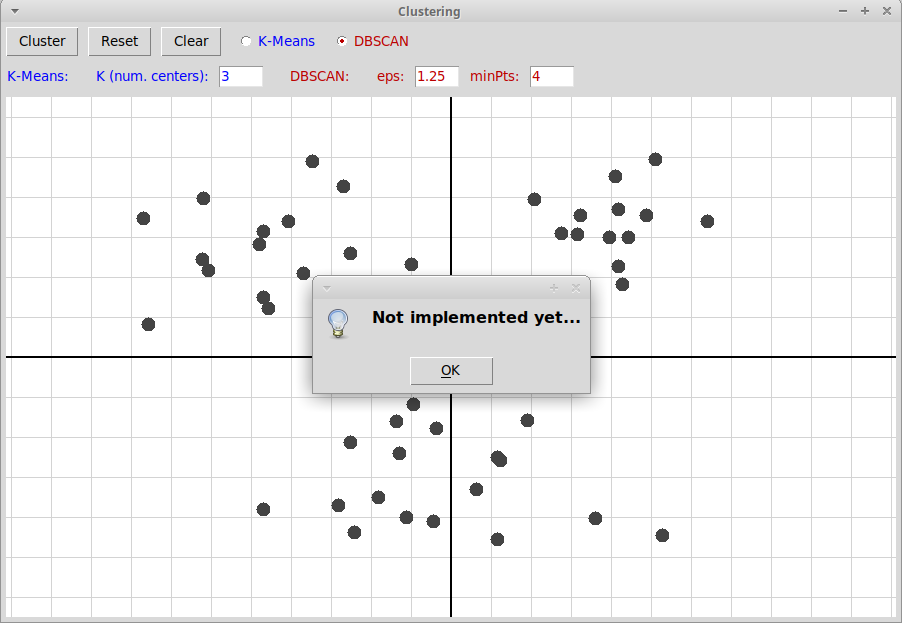
Нужно реализовать также использование алгоритма DBSCAN.
-
-
Осенний семестр 2022
Записи лекций на "виртуальной доске" (осенний семестр)
-
Домашние задания (осенний семестр)
-
Задача 1.
Решить кубическое уравнение общего вида:a x3 + b x2 + c x + d = 0,Написать функцию, которая возвращает список из трех корней уравнения.
a, b, c, d ∈ C (комплексные числа) -
Задача 2 (необязательная).
Для четного числа n вычислить количество счастливых билетов длины n. Программа должна работать как минимум для n ≤ 16. -
Задача 3. Варианты:
- Реализовать вероятностный тест простоты Миллера-Рабина.
- Реализовать алгоритм для Китайской теоремы об остатках.
- Факторизовать целое число с помощью ρ-алгоритма Полларда.
- Факторизовать целое число с помощью p-1-алгоритма Полларда (используйте упрощенный p-1 алгоритм Полларда, не требующий вычисления всех простых степеней, не превосходящих верхней границы: qiα ≤ N, вместо этого используется N!).
-
Вычислить квадратный корень из x в поле
Zp (p — простое число),
т.е. найти r такое, что
r2 ≡ x (mod p). - * Факторизовать целое число с помощью алгоритма Ленстра на эллиптических кривых.
Нужно сделать одну задачу из списка. Всего в списке 5 задач (6-я — необязательная). Студент выбирает ту задачу, которая совпадает по модулю 5 с его номером по журналу. Например, если номер по журналу 7, выбирается задача 2, если 10 — задача 5. Вместо любой задачи можно по желанию сделать задачу 6, более сложную, чем остальные.
-
Задача 4: реализация класса. Варианты:
-
Реализовать класс Polynomial, представляющий многочлен
произвольной степени с коэффициентами в поле рациональных
чисел. Должны быть реализованы операции сложения, умножения,
деления с остатком, вычисление наибольшего общего делителя
многочленов, производной многочлена, а также вычисление
многочлена с теми же корнями, свободного от кратных корней,
т.е. частного от
деления многочлена f на gcd(f, f').
Указание: в Python'е рациональные числа представлены классом Fraction в модуле fractions.
>>> from fractions import * >>> x = Fraction(3, 7) >>> y = Fraction(1, 5) >>> x + y Fraction(22, 35) -
Та же задача, но для многочленов над полем Zp.
(Следует в решении использовать класс Zm, реализующий элементы кольца вычетов по модулю m, файл "Zm.py".) -
Реализовать класс "Элементы поля GFp2",
где p — простое число.
См. Конструкция конечного поля из p2 элементов.
(Следует в решении использовать класс Zm, реализующий элементы кольца вычетов по модулю m, файл "Zm.py".)
Презентация: Классы в Python'е на примере классов R2Vector и R2Point для поддержки графики на плоскости R2.
Оба класса содержатся в модуле R2Graph, файл "R2Graph.py".Еще один несложный пример класса: класс Zm, реализующий элементы кольца вычетов по модулю m, файл "Zm.py".
-
Реализовать класс Polynomial, представляющий многочлен
произвольной степени с коэффициентами в поле рациональных
чисел. Должны быть реализованы операции сложения, умножения,
деления с остатком, вычисление наибольшего общего делителя
многочленов, производной многочлена, а также вычисление
многочлена с теми же корнями, свободного от кратных корней,
т.е. частного от
деления многочлена f на gcd(f, f').
-
Задача 5: модуль numpy и метод Гаусса. Варианты:
-
Решить систему линейных уравнений с невырожденной
квадратной матрицей. Использование функции:
x = solve(a, b)Здесь a — невырожденная квадратная матрица, b — столбец свободных членов, представленный одномерным numpy-массивом. Функция должна вернуть одномерный массив-решение x или возбудить исключение типа ValueError для вырожденной или неквадратной матрицы. Матрица a не должна изменяться.
-
Найти обратную матрицу:
b = inverse(a)Здесь a — невырожденная квадратная матрица, Функция должна вернуть обратную матрицу b или возбудить исключение типа ValueError для вырожденной или неквадратной матрицы a. Матрица a не должна изменяться.
-
Дан список векторов, векторы представляются одномерными
numpy-массивами.
Найти среди них максимальную линейно-независимую систему:
indexList = maxIndependentSystem(vectorList)Функция должна вернуть список индексов векторов из данного списка, которые образуют базис линейной оболочки этих векторов.
Во всех вариантах этой задачи используйте уже готовую функцию
(rank, det) = gauss(a)которая приводит матрицу a к ступенчатому виду и возвращает ранг и определитель матрицы (для неквадратной матрицы определитель не вычисляется и возвращается 0). Матрица a представлена в виде двумерного numpy-массива с вещественными значениями. Функция реализована в файле "gauss.py". -
Решить систему линейных уравнений с невырожденной
квадратной матрицей. Использование функции:
-
Задача 6: синтаксический разбор
Проект "Рисование графика функции"
Проект включает 3 файла: "scanner.py", "exprParser.py", "plotter.py".
Архив всех файлов проекта: "plotter.zip".Пример выполнения программы:
/home/vvb/MasterAI>python3 plotter.py Input a function: 4*sin(3*x)/(1 + x*x)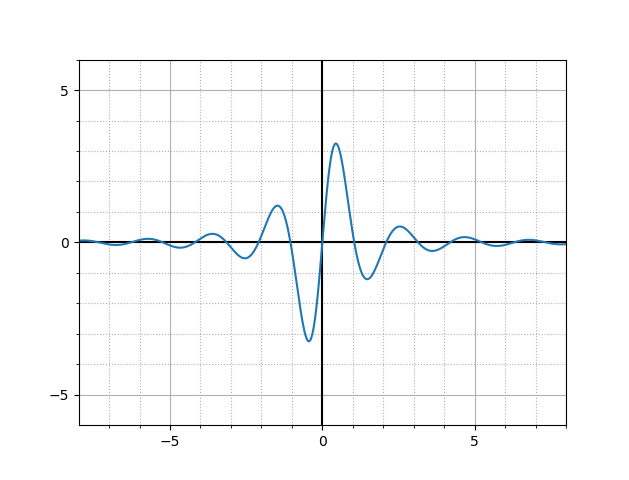
Домашнее задание
Требуется внести следующие изменения в проект "plotter":- добавить унарный минус в грамматику (операция изменения знака);
- добавить константы pi, e;
- добавить операцию возведения в степень, которая обозначается либо как в Питоне **, либо как в математике и в SageMath "^": например, квадрат синуса от х записывается как sin(x)^2 (этот пункт требует изменений и в сканере, и в парсере).
-
Задача 1.
-
Задача 7. Программирование оконных приложений на Питоне с помощью модуля tkinter
Список вариантов
-
Нарисовать треугольник, вписанную окружность и точку Жергона.
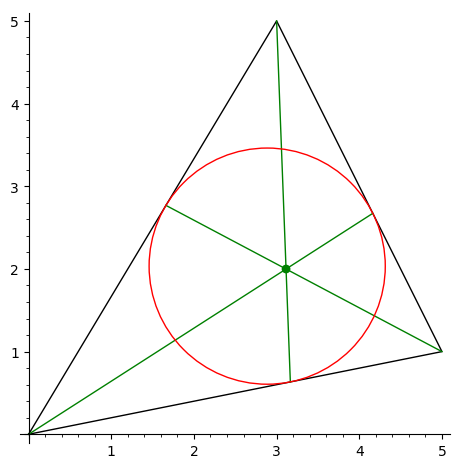
-
Нарисовать треугольник, три внешне вписанных окружности и точку Нагеля.
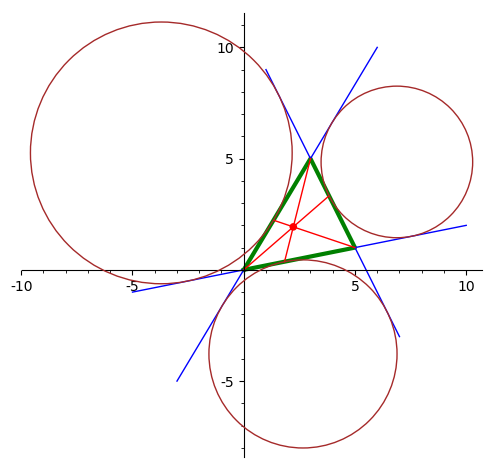
-
Нарисовать треугольник и точку Лемуана, которая построена как
точка, изогонально сопряженная к точке пересечения медиан.
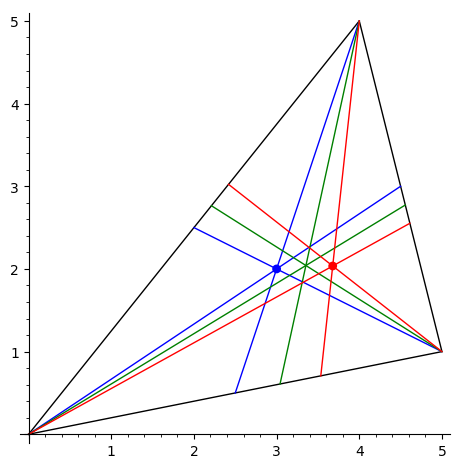
-
Нарисовать треугольник и точку Ферма-Торичелли (точка, минимизирующая
сумму расстояний до вершин треугольника), изобразив процесс ее
построения.
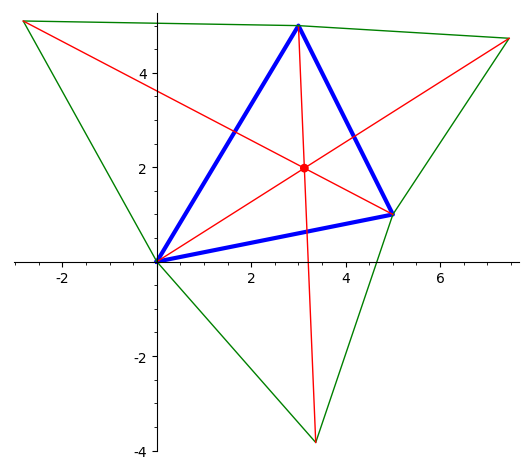
-
Нарисовать треугольник, вписанную окружность и точку Жергона.
Журнал группы, осенний семестр 2022
Материалы прошлого года
- Осенний семестр 2021
-
Весенний семестр 2022
-
Семинар 11.02.2022
Метод наименьших квадратов -
Семинар 18.02.2022
Градиентный спуск и его ускоренные варианты -
Семинар 25.02.2022
Метод опорных векторов -
Семинар 18.03.2022
Стохастический градиентный спуск -
Семинар 25.03.2022
Нелинейный вариант метода опорных векторов: увеличение размерности пространства признаков путем добавления всех мономов степени не выше d и применение классического метода опорных векторов в пространстве увеличенной размерности -
Семинар 1.04.2022
Ядровые методы и их использование в нелинейном методе опорных векторов -
Семинар 8.04.2022
Борьба с выбросами: использование функции потерь Хубера в задаче линейной регрессии -
Семинар 15.04.2022
Решение задачи линейной регрессии методами линейного программирования -
Семинар 29.04.2022
Метод главных компонент
-
Семинар 11.02.2022
Журнал группы, весенний семестр 2022
Осенний семестр 2022 г.
Материалы к семинарам
- Семинар 14.09.2022. Введение в Python
Семинар 1, 14 сентября 2022
Домашнее задание
Написать на Питоне функцию, решающую кубическое уравнение общего вида:
Как вывести формулу Кардано: способ решения кубического уравнения. Любое кубическое уравнение сводится к уравнению вида
def solveCubicEquation(a, b):
'''Solve cubic equation x^3 + a*x + b = 0'''
a = complex(a)
b = complex(b)
d = (27*b)**2 + 4*27*a**3
y = (-27*b + d**(1/2))/54
u = y**(1/3)
v = -a/(3*u)
x = u + v
return x
Файл с программой на Питоне, которую можно использовать и как модуль,
и как скрипт:
"cubeq.py"
Материалы семинара
Python — язык, придуманный Гвидо Россумом, максимально удобный для использования. Его почти не надо учить, выражения языка максимально приближены к формулам, которые используются в математике. Обычные этапы постороения программы на, допустим, языке C/C++ — компиляция отдельных модулей и сборка программы — в языке Python отсутствуют (вернее, они выполняются незаметно для пользователя). Интерпретатор Питона позволяет использовать язык как продвинутый калькулятор (быстро вычислить нужную величину, нарисовать график функции и т.п.); кроме того, в интерпретаторе можно быстро проверить синтаксис и семантику выражений Питона, посмотреть подсказку по функциям и классам и т.д. Все это сделало язык очень популярным в последнее время. В частности, почти весь код, связанный с искусственным интеллектом, традиционно пишется на Питоне и для Питона.
Базовые типы объектов и выражений в Питоне
Python — объектно ориентированный язык с динамической типизацией. Переменные в Питоне не имеют типа, и вообще отсутствуют операторы описания типов. Тип выражения определяется только в момент выполнения программы. Встроенные оператор type позволяет во время выполнения получить тип объекта или выражения:
>>> type(123)
<class 'int'>
>>> type("Hello!")
<class 'str'>
>>> type((-1)**(1/2))
<class 'complex'>
>>> type(0.5)
<class 'float'>
>>> type(2 + 2 == 4)
<class 'bool'>
Базовые типы — это целые числа int, вещественные числа float,
комплексные числа complex, логические выражения bool
(они могут принимать значения True и False) и текстовые строки str.
Целые числа в Питоне
не ограничены:
>>> 3**70
2503155504993241601315571986085849
Это очень удобно для реализации различных алгоритмов теории чисел.
Операция возведения в степень обозначается в Питоне двумя звездочками
**. Кроме того, имеется встроенная функция pow. Если она применяется к трем
целочисленным аргументам, то степень вычисляется в кольце вычетов
по модулю последнего аргумента:
>>> 2**10
1024
>>> pow(2, 10, 100)
24
Комплексная мнимая единица обозначается через j.
Операция возведения в степень применима и к комплексным числам,
в частности, она может быть использована для извлечения корня
n-й степени:
>>> (-1)**(1/2)
(6.123233995736766e-17+1j)
>>> (1j)**(1/3)
(0.8660254037844387+0.49999999999999994j)
Списки и кортежи
. . .
Весенний семестр 2022 г.
Материалы к семинарам
- Семинар 11.02.2022. Метод наименьших квадратов
- Семинар 18.02.2022. Градиентный спуск и его ускоренные варианты
- Семинар 25.02.2022. Метод опорных векторов
- Семинар 18.03.2022. Стохастический градиентный спуск
- Семинар 25.03.2022. Нелинейный вариант метода опорных векторов: увеличение размерности пространства признаков путем добавления всех мономов степени не выше d и применение классического метода опорных векторов в пространстве увеличенной размерности
- Семинар 1.04.2022. Ядровые методы и их использование в нелинейном методе опорных векторов
- Семинар 8.04.2022. Борьба с выбросами: использование функции потерь Хубера в задаче линейной регрессии
- Семинар 15.04.2022. Решение задачи линейной регрессии методами линейного программирования
- Семинар 29.04.2022. Метод главных компонент
Семинар 1, 11 февраля 2022
Создание оконных приложений на языке Python3 с использованием модуля tkinter. Реализация на Python3 оконного интерактивного приложения, иллюстрирующего метод наименьших квадратов.
Домашнее задание
Реализовать на языке Python3 с использованием модуля tkinter интерактивное приложение, иллюстрирующее метод наименьших квадратов.
Пользователь отмечает кликами мыши множество точек на координатной плоскости,
точки отмечаются крестиками. С помощью слайдера в оконной форме задается
степень аппроксимирующего многочлена. По нажатию на кнопку "Draw"
программа вычисляет коэффициенты аппроксимирующего многочлена,
применяя метод наименьших квадратов, и рисует его график в окне:

Описание метода наименьших квадратов
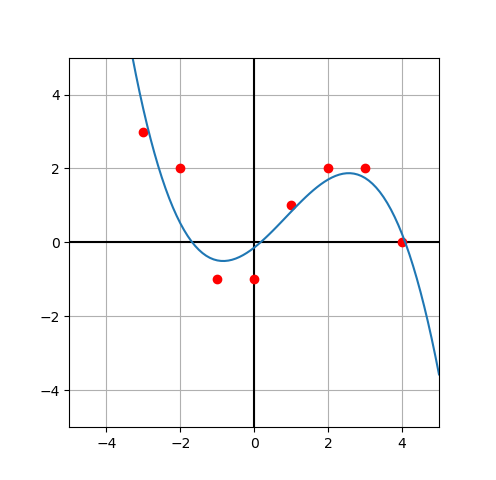
Создание оконных приложений в Python'е с помощью модуля tkinter
Модуль tkinter предоставляет, наверно, самый простой из всех возможных
интерфейсов для создания интерактивных оконных приложений на языке
Python. Рассмотрим пример простейшей оконной программы, которую
можно использовать как заготовку для создания собственных приложений.
Программа создает окно-форму верхнего уровня,
в верхней части которого расположены
управляющие элементы, в нашем случае две кнопки "Draw" и "Clear".
Также в верхней части окна расположен слайдер, с помощью которого
можно изменять значение целочисленной переменной (мы будем ее использовать
для задания степени многочлена, аппроксимирующего зависимость между
переменными x и y в методе наименьших квадратов). В нижней части
окна верхнего уровня расположено дочернее окно, предназначенное для рисования.
В нем изображена координатная сетка.
По нажатию кнопки "Draw" в нем рисуется
график функции, заданной непосредственно в тексте
программы. Также можно в этом окне кликать мышкой, программа в ответ рисует
крестики в этих точках; цвет крестика соответствует
номеру нажатой клавиши мыши. Нажатие кнопки "Clear" в верхней части
стирает график функции и крестики в отмеченных точках.
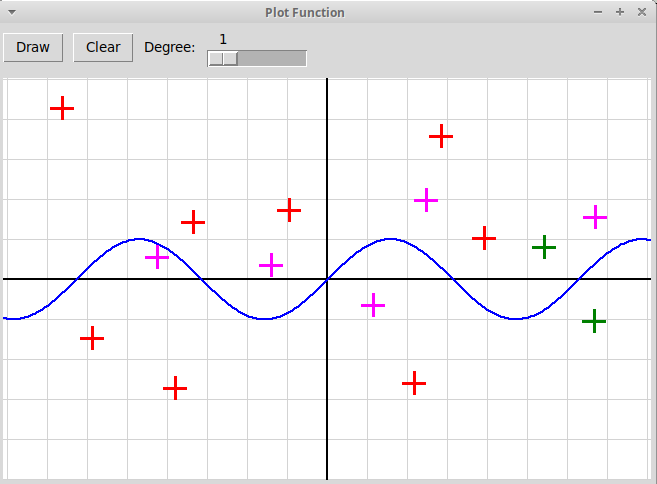
Приложение использует два файла: файл "plotFunc.py" содержит непосредственно саму оконную программу; файл "R2Graph.py" содержит определения классов Вектор и Точка на плоскости R2Vector и R2Point, которые используются в программе. Файл R2Graph.py импортируется в оконной программе как вспомогательный модуль. Архив всех файлов: "plotFunc.zip".
Запускается программа командой
python3 plotFunc.py
Семинар 2, 18 февраля 2022
Минимизация функций. Метод градиентного спуска.
Ускоренные методы: метод тяжелого шарика Поляка,
ускоренный метод Нестерова
Интерактивная оконная программа на Python'е с использованием модуля tkinter, иллюстрирующая разные методы градиентного спуска. В ней можно задавать в текстовом поле минимизируемую функцию f(x, y) и параметры методов (размер шага Learning Rate и степень инерции шарика Momentum). В окне изображаются линии уровня функции. По клику мыши изображается траектория по точкам итерации, которая приводит в точку локального минимума. По нажатию на левую клавишу мыши используется классический метод градиентного спуска; по средней клавише запускается метод тяжелого шарика; по правой клавише мыши запускается метод Нестерова, наиболее популярный в настоящее время.

Домашнее задание
Дается готовая оконная программа на Python3 + tkinter
"gradientDescent.py",
иллюстрирующая метод градиентного спуска
(программа использует также модули
lparser и R2Graph),
архив всех файлов:
"gradientDescent.zip".

В программе реализован только метод градиентного спуска
(запускается по клику левой клавиши мыши),
для методов Тяжелого шарика и
Ускоренного метода Нестерова оставлены заглушки.
Требуется добавить в программу реализацию этих двух методов.
Метод Тяжелого шарика запускается по клику средней клавиши мыши
(траектория и текст изображаются синим цветом),
Ускоренный метод Нестерова запускается по клику правой клавиши мыши
(используется зеленый цвет).
Описание метода градиентного спуска и его ускоренных вариантов
Ускоренные методы градиентного спуска: метод тяжелого шарика Поляка и ускоренный метод Нестерова. Преимущества этих методов: 1) меньшая вероятность осцилляций; 2) значительно более быстрая сходимость. Наилучшим является метод Нестерова.
Подробное описание этих методов см. здесь. Выпишем еще раз коротко формулы, которые используются при вычислении очередной точки итерации в каждом из этих методов.
Мы ищем минимум функции f(x), где x — точка n-мерного пространства Rn. Через x0 обозначается точка начального приближения. В каждом из этих трех алгоритмов вычисляется последовательность приближений x0, x1, x2, ... Используются следующие параметры:
где L — константа Липшица для градиента функции f(x)
(обычно α выбирается равным 1/L);
β — степень инерции, или "момент" (momentum), 0 ≤ β < 1.
-
Классический метод градиентного спуска:
xk+1 = xk − α ∇f(xk)
-
Метод тяжелого шарика:
xk+1 = xk − α ∇f(xk) + β (xk − xk-1)
-
Ускоренный метод Нестерова:
yk = xk + β (xk − xk-1)
xk+1 = yk − α ∇f(yk)
Семинар 3, 25 февраля 2022
Метод опорных векторов
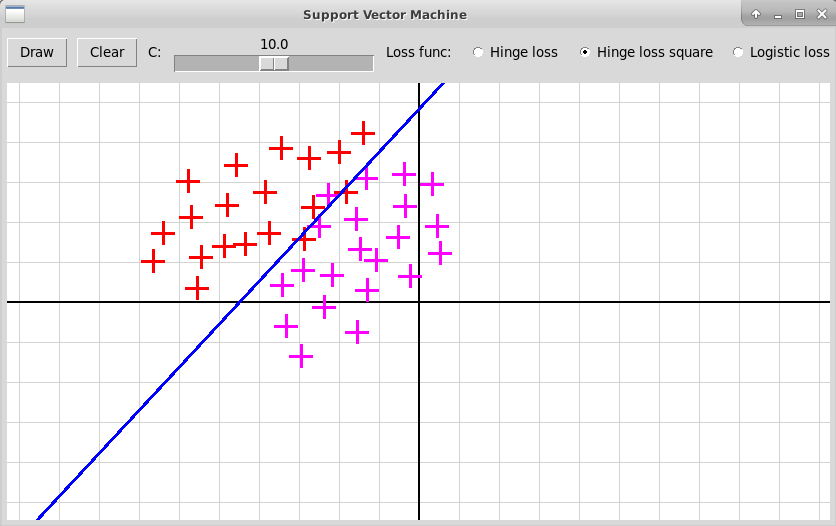
Описание метода опорных векторов (Support Vector Machine)
Домашнее задание
Применить линейный классификатор, основанный на методе опорных векторов, для классификации рукописных цифр из тестовой базы (см. лекцию):
from sklearn.datasets import load_digits digits = load_digits()При этом не использовать библиотечные вызовы:
from sklearn import linear_model from sklearn.svm import LinearSVC as SVCПопробовать обойтись только функцией minimize модуля scipy.optimize:
import scipy.optimize as opt . . . ans = opt.minimize(lossFunction, x0) solution = ans.xРазделить исходный массив данных (матриц рукописных цифр) на тренировочную и проверочную части. Для классификации использовать сначала метод "один против остальных" (one-vs.-rest), затем метод "каждый против каждого" (one-vs.-one). В качестве функции потери использовать 3 варианта: hinge loss, hinge loss square, logistic loss; также использовать набор фиксированных значений параметра С (обратного к коэффициенту регуляризации), например, [1., 5., 10., 20.]. Найти, при каком сочетании разных методов и параметров достигается наилучший результат по показателю "precision" (процент цифр, определенных правильно).
Семинар 4, 18 марта 2022
Стохастический градиентный спуск
1) определение линейной или полиномиальной регрессии в методе наименьших квадратов;
2) вычисление линейного классификатора в методе опорных векторов.
Описание метода стохастического градиентного спуска
Следующее изображение показывает окно
графической программы sgdLeastSquares.py,
иллюстрирующей применение стохастического градиентного спуска
в методе наименьших квадратов. Ищется квадратичная зависимость между
независимой переменной x и зависимой переменной y.
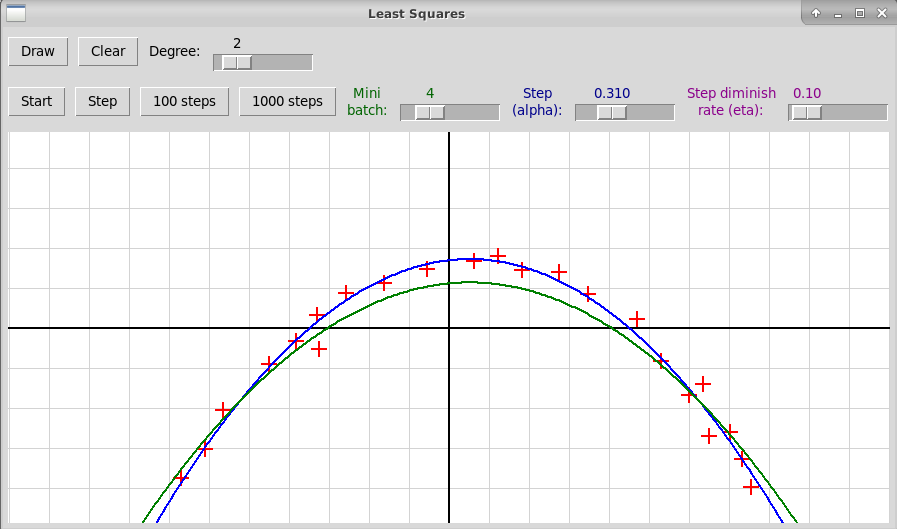
Синим цветом нарисована парабола, вычисленная точным методом
с использованием псевдообратной матрицы. Зеленым цветом изображено решение,
найденное методом SGD, число шагов здесь равно 2000, а размеры шагов
заданы параметрами α и η и вычисляются по формуле
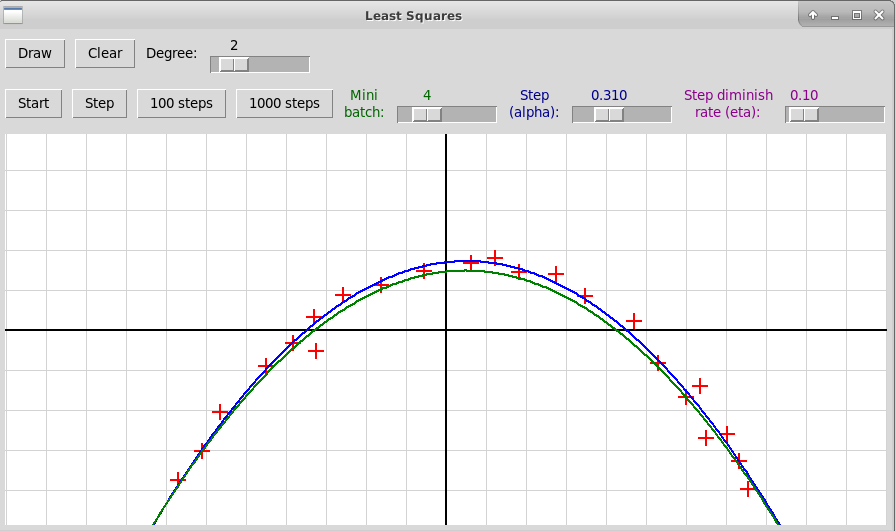
Эксперименты с данной программой показывают, что метод очень чувствителен к
начальному размеру шага (параметр α) и вообще к сочетанию
параметров α, η. Например, при значениях
α=0.500, η=0.10 метод расходится. Сходимость довольно
медленная, например, в данном случае при значениях
параметров α=0.310, η=0.10
удовлетворительный результат достигается только при 8000 итерациях:
Домашнее задание
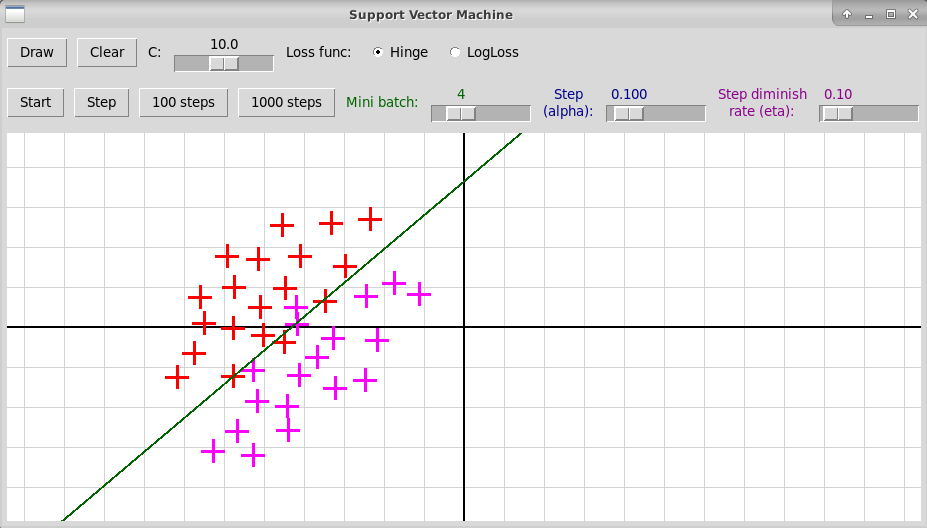
Реализовать самостоятельно программу sgdLeastSquares.py, которая находит полиномиальную зависимость между переменными x, y методом стохастического градиентного спуска. В качестве образца можно использовать программу sgdSVM.py, в которой метод стохастического градиентного спуска применяется для вычисления линейного классификатора в методе опорных векторов. Архив исходных текстов программы: "sgdSVM.zip".
Вот изображение работы программы
sgdSVM.py:
Семинар 5, 25 марта 2022
Нелинейный вариант метода опорных векторов:
увеличение размерности пространства признаков путем добавления
всех мономов от исходных признаков степени не выше d
и применение классического метода опорных векторов в пространстве
увеличенной размерности
Программа, иллюстрирующая графически нелинейный метод опорных векторов.
В классическом методе опорных векторов мы имеем два класса объектов, каждый объект описывается n признаками, представляемыми вещественными числами. Таким образом, объекты x1, x2, … xk представляются точками n-мерного пространства; координаты такой точки равны значениям признаков объекта. В тренировочной выборке объекты xi первого класса отмечены значением yi = 1, объекты xj второго класса — значением yj = -1. В методе опорных векторов SVM (Support Vector Machine) строится линейный классификатор f(x), который определяется как гиперплоскость, разделяющая два класса точек:
x, w ∈ Rn, b ∈ R.
В классическом методе опорных векторов далеко не всегда можно разделить
гиперплоскостью два класса точек в n-мерном пространстве:
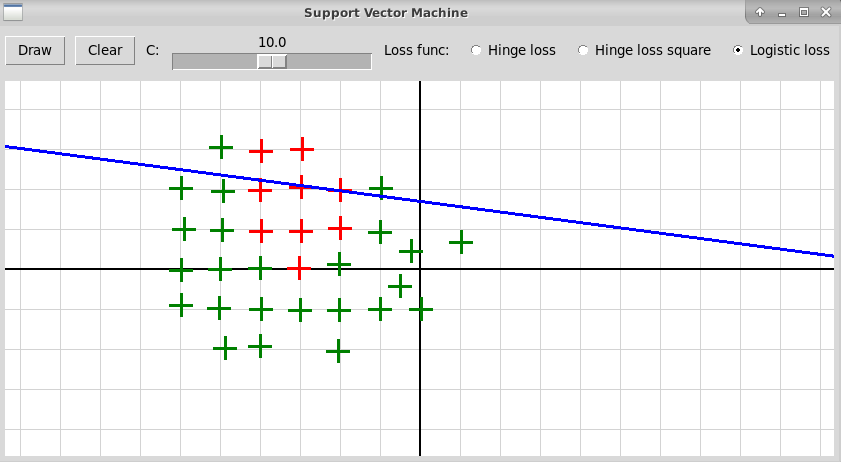
Идея нелинейного метода опорных векторов состоит в том, чтобы дополнить
исходный набор из n признаков объекта дополнительными признаками,
которые вычисляются как некоторые функции от набора исходных признаков.
В результате мы получим
множество точек в пространстве более высокой размерности, где каждая точка
представляет расширенный набор признаков исходного объекта. Можно надеяться,
что в пространстве более высокой размерности эти точки уже можно
разделить гиперплоскостью.
Итак, пусть отображение
φ(x) = (φ1(x), φ2(x), … φm(x)), где x = (x1, x2, … xn),
В простейшем случае в качестве функций φ1(x1, … xn), φ2(x1, … xn), …, φm(x1, … xn) можно взять всевозможные мономы степени не выше d от переменных x1, x2, … xn (то есть от исходных признаков).
Пусть, например, d = 2. Пусть число исходных признаков n = 2, т.е. объекты представляются точками плоскости R2. Тогда расширенный набор признаков представляется всеми мономами степени не выше 2 от переменных x1, x2:
Программа "svmKernel.py" иллюстрирует использование нелинейного метода опорных векторов, архив всех исходных файлов программы "svmKernel.zip". Исходные объекты представляются точками плоскости двух цветов, отмечаемые кликами левой и правой клавиш мыши. В качестве расширенных признаков используются все мономы степени не выше d от координат x и y очередной точки; степень d задается с помощью слайдера в пределах от 1 до 5. Программа после построения нелинейного классификатора f(x) изображает линию нулевого уровня функции
Классический случай: степень 1
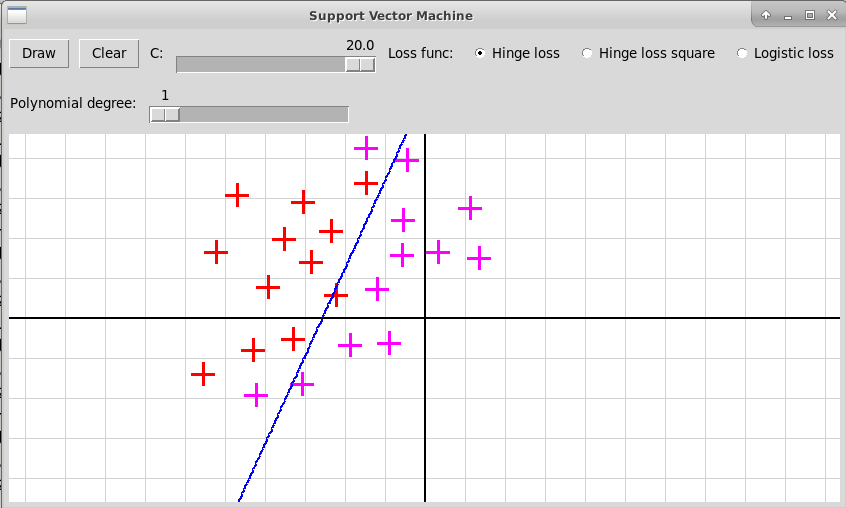
Квадратичные мономы: степень 2
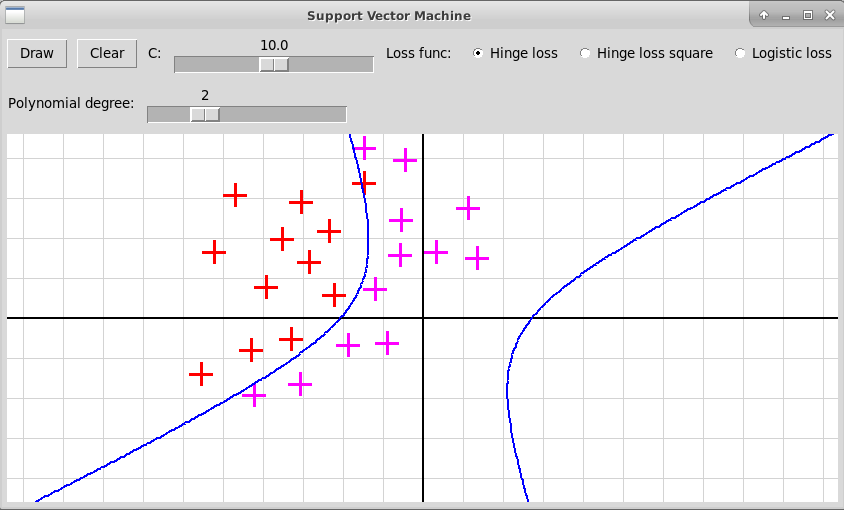
Кубический многочлен: степень 3
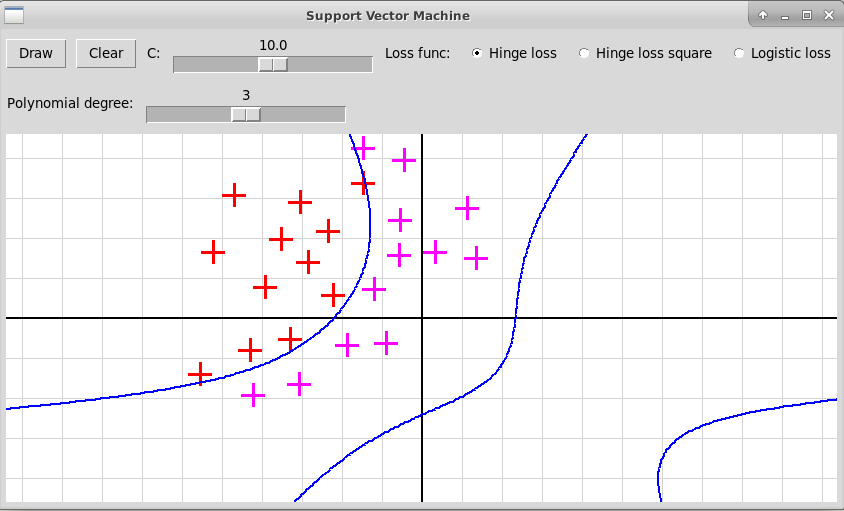
Многочлен степени 4
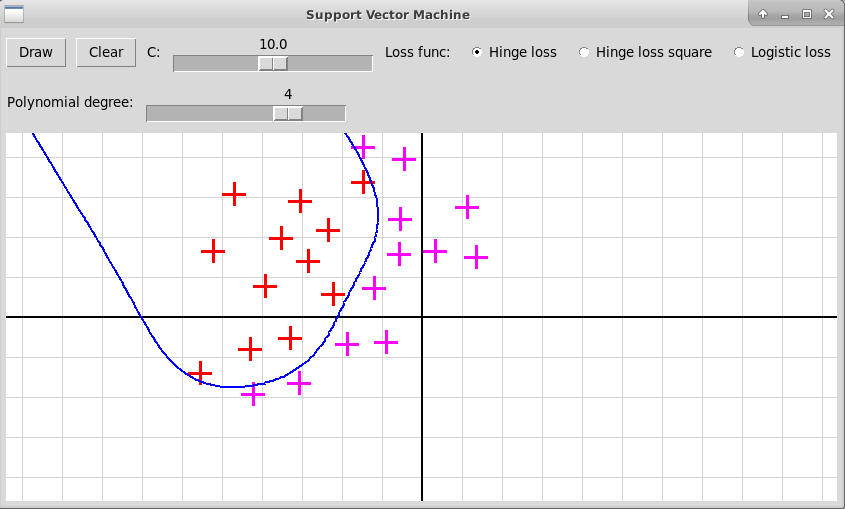
Многочлен степени 5
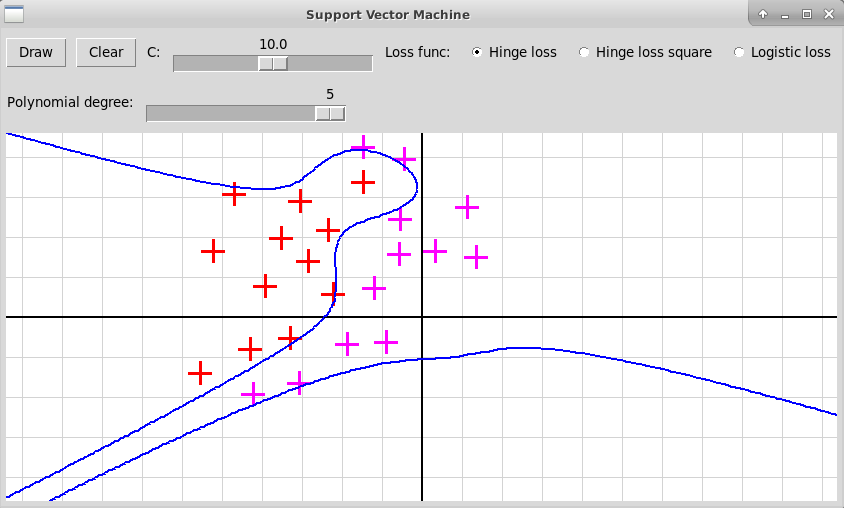
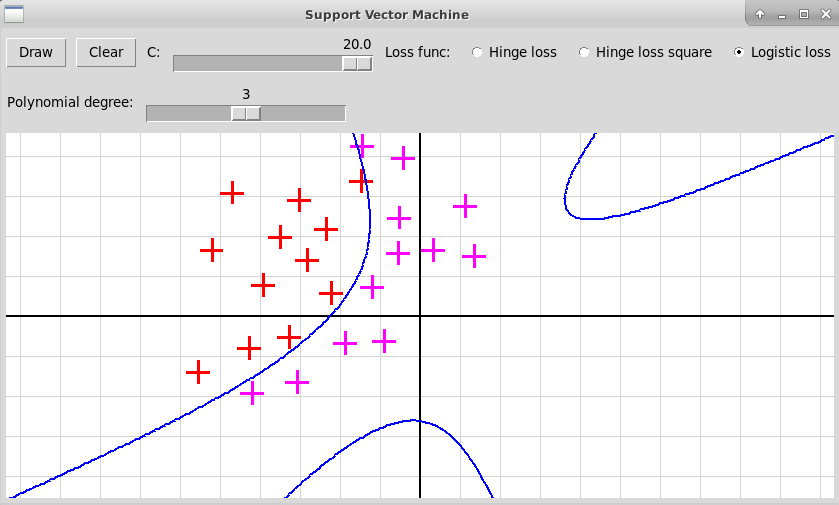
В случае полинома высокой степени 5 мы, скорее всего, наблюдаем переобучение. Также форма разделяющей кривой сильно заисит от гиперпараметра С и от функции потери, что иллюстрируется следующими скриншотами:
-
Степень полинома 3, функция потерь Hinge Loss, C=10:

-
Степень полинома 3, функция потерь Hinge Loss, C=20:
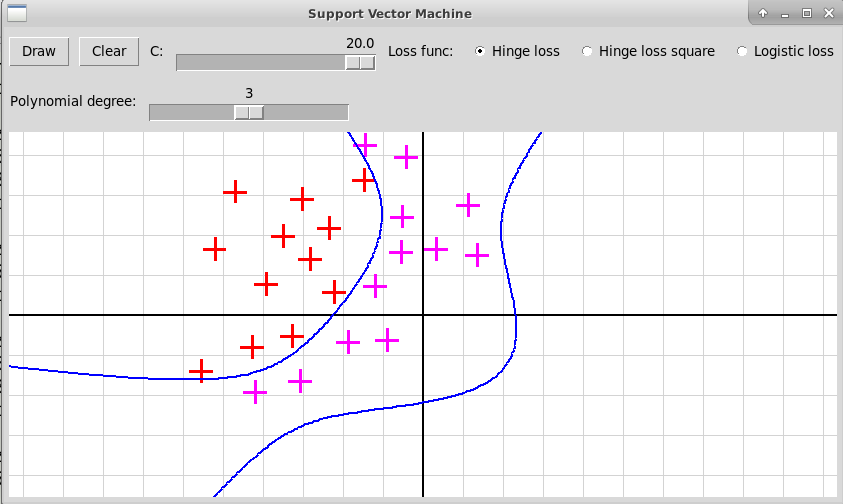
-
Степень полинома 3, функция потерь Logistic Loss, C=20:
-
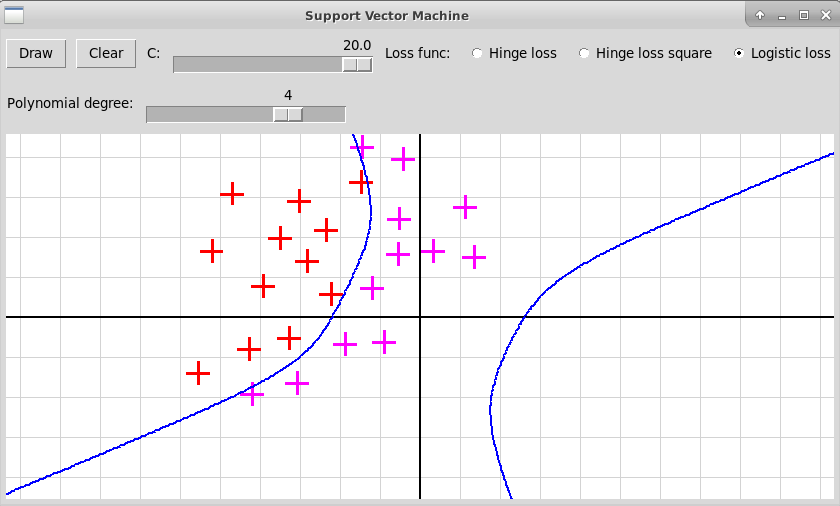
Степень полинома 4, функция потерь Hinge Loss, C=10:

-
Степень полинома 4, функция потерь Logistic Loss, C=20:
Программа на Питоне (подготовленная в Jupyter-Lab), иллюстрирующая нелинейный метод опорных векторов
#!/usr/bin/env python
# coding: utf-8
# Nonlinear Support Vector Machine
import numpy as np
import matplotlib.pyplot as plt
import random
from scipy.optimize import minimize
from skimage import measure
import itertools
from math import sin, cos, pi
d = 3
C = 5.
def monomials(x, d):
'''Return an array of all products of degree <= d
composed from the coordinates of vector x'''
# m = [1.]
m = []
for l in range(1, d+1):
for i in itertools.combinations_with_replacement(x, l):
v = np.prod(i)
m.append(v)
return np.array(m)
def f(x):
'''Graph of this function separates two classes of points'''
return 3.*sin(0.5*x) + 1.
# xmin = -10.; xmax = 10.;
# ymin = -10.; ymax = 10.;
m = 100
class1 = []
class2 = []
for i in range(m):
x1 = random.normalvariate(0., 4.)
y1 = f(x1) + random.normalvariate(3., 2.)
class1.append([x1, y1])
x2 = random.normalvariate(0., 4.)
y2 = f(x2) - random.normalvariate(3., 2.)
class2.append([x2, y2])
x = np.array(class1 + class2)
# print("x:", x)
y = np.array([1.]*m + [-1.]*m)
# print("y:", y)
# %matplotlib inline
# get_ipython().run_line_magic('matplotlib', 'inline')
ax = plt.gca()
ax.set_aspect("equal")
# ax.set_xlim(-10., 10.)
# ax.set_ylim(-10., 10.)
ax.scatter(
[xx[0] for xx in x],
[xx[1] for xx in x],
color = [("red" if yy > 0 else "green") for yy in y]
)
xext = np.array([monomials(xx, d) for xx in x])
k = len(xext[0])
print("Polynomial degree =", d)
print("Dimension of extended space =", k)
# Shuffle the training base
perm = np.random.permutation(2*m)
x = x[perm]
xext = xext[perm]
y = y[perm]
def hingeLoss(x):
return max(1. - x, 0.)
def lossFunction(wb):
'''Loss function to be minimized in Support Vector Machive'''
n = len(xext)
w = wb[:-1]
b = wb[-1]
s = 0.
for i in range(n):
c = y[i]*(w @ xext[i] - b)
l = hingeLoss(c)
s += l
err = w@w + (C/n)*s
# print("w:", w, "b:", b, "err:", err)
return err
wb = np.array([0.]*k + [0])
res = minimize(lossFunction, wb)
# print("res;", res)
w = res.x[:-1]
b = res.x[-1]
print("Parameters of linear classifier in extended space:")
print("w =", w)
print("b =", b)
def classifier(x):
'''Linear classifier constructed by SVM method'''
xe = monomials(x, d)
return w@xe - b
# Draw the isoline defined by the equation
# classifier(x) = 0
xmin = min([xx[0] for xx in x]) - 1.
xmax = max([xx[0] for xx in x]) + 1.
ymin = min([xx[1] for xx in x]) - 1.
ymax = max([xx[1] for xx in x]) + 1.
dx = 0.1; dy = dx
xSteps = int((xmax - xmin)/dx)
ySteps = int((ymax - ymin)/dy)
def xcoord(j):
return xmin + j*dx
def ycoord(i):
return ymin + i*dy
# Matrix of function values
a = [[0.]*xSteps for i in range(ySteps)]
a = np.array(a)
for i in range(ySteps):
y = ycoord(i)
for j in range(xSteps):
x = xcoord(j)
v = classifier(np.array([x, y]))
a[i, j] = v
contours = measure.find_contours(a, 0.)
for contour in contours:
ax.plot(
[xcoord(c[1]) for c in contour],
[ycoord(c[0]) for c in contour],
color="blue"
)
plt.show()
Вот результат работы этой программы (запущенной в среде Jupyter-Lab):
w = [-0.41272467 0.17345086 -0.02273882 -0.06216637 0.02002704
0.0116851 0.01637095 -0.01324022 0.02169916]
b = 0.44400368280740304
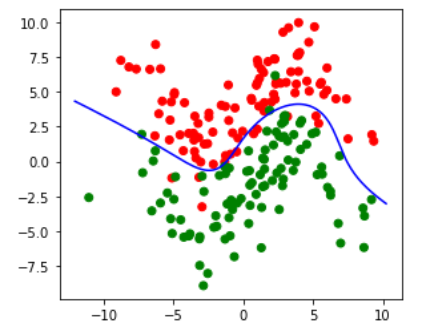
Исходный код программы
- в формате jupyter notebook: "NonlinearSVM.ipynb"
- в формате python script: "NonlinearSVM.py"
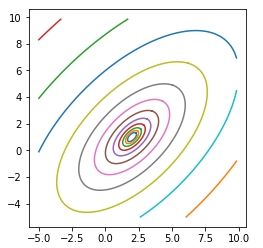
Эта же программа иллюстрирует изображение линий уровня (изолиний, изогипс) функции от двух переменных
# Drawing Isolines
import numpy as np
import matplotlib.pyplot as plt
from skimage import measure
get_ipython().run_line_magic('matplotlib', 'inline')
plt.axes(aspect="equal")
def f(x, y):
return ((x - 2) + (y - 1))**2/4 + ((x - 2) - (y - 1))**2
xmin = -5.; xmax = 10.
ymin = -5.; ymax = 10.
m = 100; n = 100
def xcoordinate(j):
dx = (xmax - xmin)/n
x = xmin + j*dx
return x
def ycoordinate(i):
dy = (ymax - ymin)/m
y = ymin + i*dy
return y
a = np.array([[0.]*n for i in range(m)])
for i in range(m):
y = ycoordinate(i)
for j in range(n):
x = xcoordinate(j)
a[i, j] = f(x, y)
for l in range(20):
level = 0.1*(2**l)
contours = measure.find_contours(a, level)
for c in contours:
plt.plot(
[ xcoordinate(cc[1]) for cc in c ],
[ ycoordinate(cc[0]) for cc in c ]
#, color="blue"
)
Вот результат работы этой программы (запущенной в среде Jupyter-Lab):
Семинар 6, 1 апреля 2022
Ядровые методы и их использование в нелинейном методе
опорных векторов
Когда мы заменяем обычное скалярное произведение некоторым ядром, представляющим собой скалярное произведение векторов, составленных из набора базисных функций от исходных признаков, то в результате решения задачи минимизации функции потерь мы получаем нелинейный классификатор. При этом, несмотря на увеличение размерности пространства признаков, сложность вычислений остается такой же, как и в случае исходной линейной задачи.
Описание ядрового варианта метода опорных векторов
Вот несколько скриншотов оконной программы на Python+tkinter,
иллюстрирующей применение ядрового метода опорных векторов:
Гауссовское ядро (RBF)
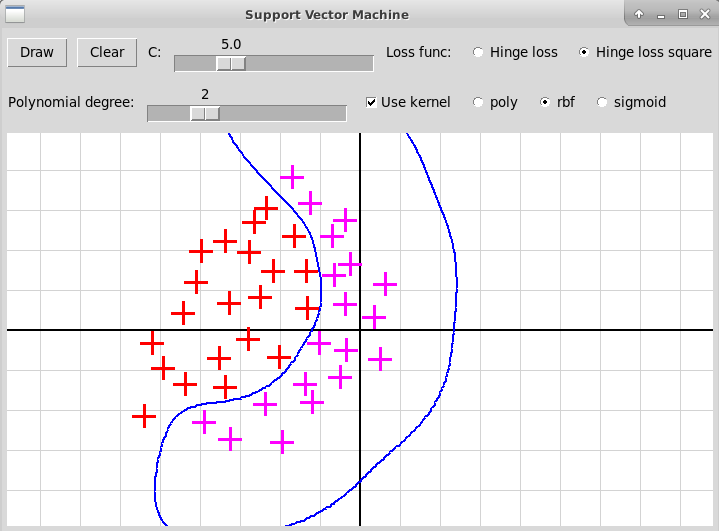
Полиномиальное ядро, степень 2
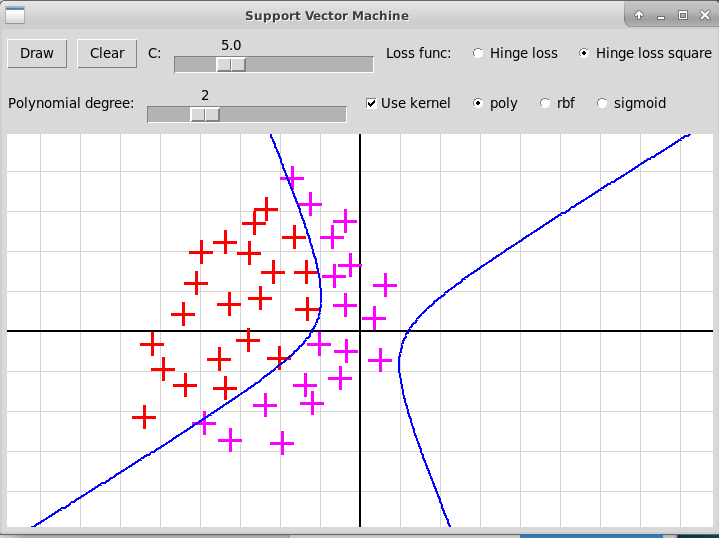
Полиномиальное ядро, степень 3
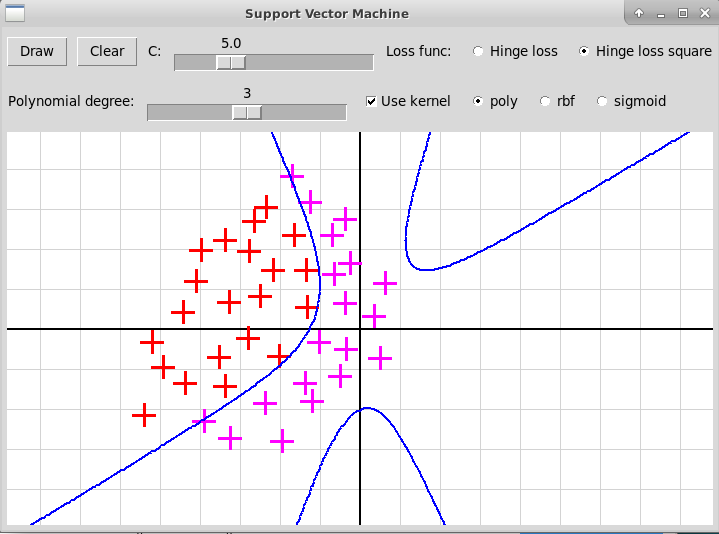
В этой программе используется модуль sklearn и его подмодуль svm, в котором реализован ядровый метод опорных векторов. В программе кликами мыши задается массив точек points, при этом точки, отмеченные кликом левой клавиши мыши, относятся к первому классу, другой клавишей — ко второму, номера клавиш мыши содержится в массиве mouseButtons. Вот как выглядит код, вызывающий метод опорных векторов.
Описания и глобальные переменные:
import numpy as np from sklearn.svm import SVC classifier = SVC(kernel="rbf")Обучение классификатора на тренировочной выборке:
global classifier
. . .
if kernel == "rbf":
classifier = SVC(C=c, kernel="rbf")
elif kernel == "poly":
classifier = SVC(C=c, kernel="poly", degree=polynomialDegree)
else:
classifier = SVC(C=c, kernel="sigmoid")
data = [
np.array(
[points[i].x, points[i].y],
)
for i in range(len(points))
]
data = np.array(data)
y = [
(1. if mouseButtons[i] == 1 else (-1.))
for i in range(len(points))
]
y = np.array(y)
classifier.fit(data, y)
Для определения класса точки p
можно использовать два метода классификатора:1) метод classifier.predict(x) возвращает 1 для первого класса и -1 для второго;
2) метод decision_function(x) возвращает значение, пропорциональное расстоянию со знаком от точки x до разделяющей гиперплоскости. Для более точного рисования линии уровня естественно использовать именно этот метод.
def classifierValue(p):
x = np.array([[p.x, p.y]])
# return classifier.predict(x)
return classifier.decision_function(x)
Используя значения, возвращаемые классификатором для точек плоскости, программа рисует линию нулевого уровня этой функции, заданную уравнением
Домашнее задание
Переделать программу
"svmKernel.py",
иллюстрирующую использование нелинейного метода опорных векторов
путем дополнения признаков объектов всеми мономами
степени не выше заданной от исходных признаков.
Архив всех исходных файлов программы:
"svmKernel.zip".
Вот скриншот работы этой программы:
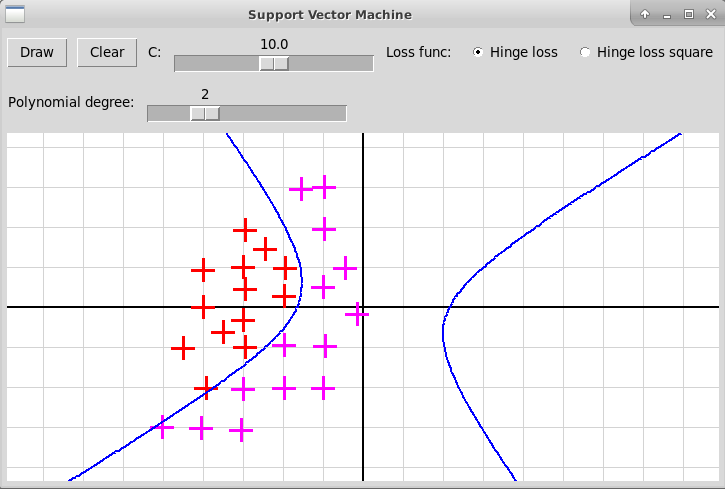
Переделанная программа должна выглядеть примерно так:
используется полиномиальное ядро степени 2
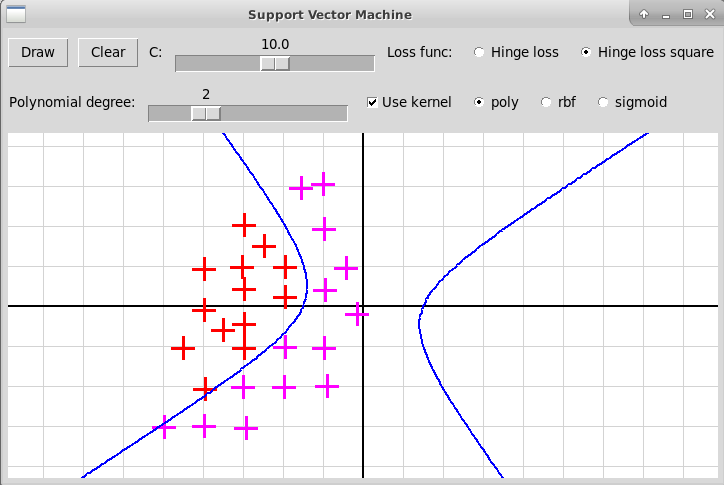
используется гауссовское ядро RBF
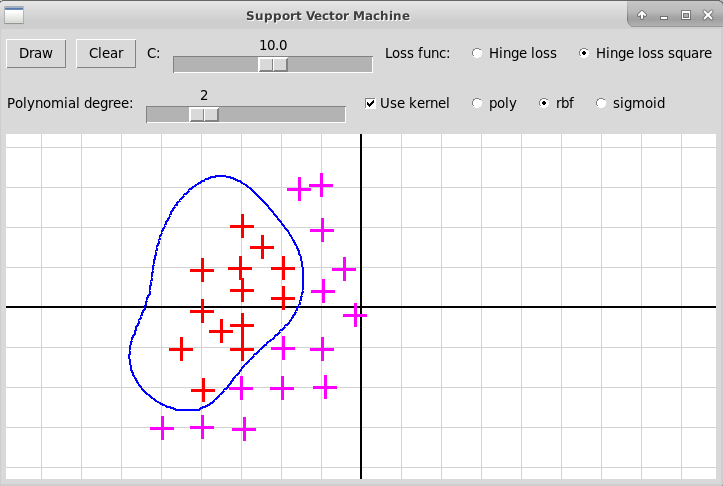
Семинар 7, 8 апреля 2022
Борьба с выбросами: использование функции потерь Хубера
в задаче линейной регрессии
В задаче линейной регрессии мы строим зависимость между независимой переменной x∈Rn и зависимой переменной y∈R. Зависимость описывается вектором w∈Rn и свободным членом b∈R:
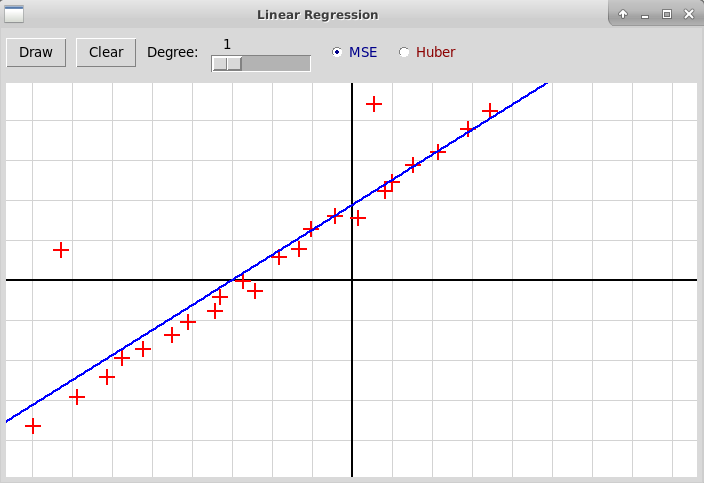
Из-за двух выбросов построенная линия заметно отклоняется от линии, вдоль которой располагаются "регулярные" точки.
Если вместо средней величины квадрата разности для каждого измерения минимизировать абсолютную величину разности, то построенная модель будет в значительно меньшей степени зависеть от выбросов. Среднее значение абсолютной величины ошибки обозначается через MAE (Mean Absolute Error):
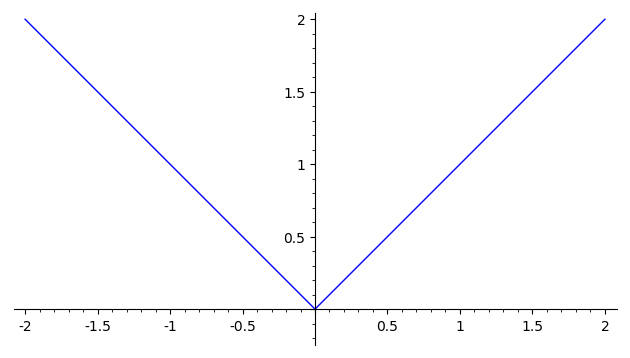
Это мешает применять алгоритмы минимизации (градиентный спуск, метод сопряженных градиентов и др.), как правило, предполагающие, что минимизируемая функция дифференцируема.
Хорошим компромиссом является использование функции потерь Хубера, зависящей от параметра δ:
| Hδ(x) = | { |
|
На следующей картинке изображен график функции Хубера для δ=1
(синий цвет), а также графики функций y = |x|
(красный) и y = x2/2 (зеленый):
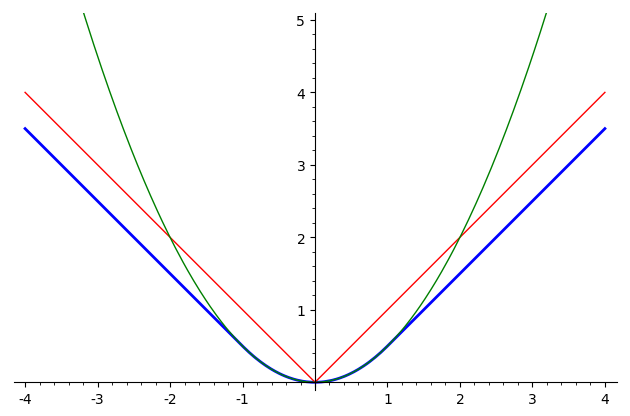
Видно, что функция потерь Хубера объединяет в себе лучшие свойства
квадратичной функции ошибки и функции абсолютной величины ошибки:
она всюду дифференцируема, так же как квадратичная функция,
но при этом не растет чрезмерно быстро, как и абсолютная величина.
В задаче регрессии модель строится путем минимизации функции средней
ошибки, вычисление которой использует
функцию потери Хубера Hδ(x):
На следующей картинке синим цветом изображена прямая,
построенная по заданной выборке
с помощью метода наименьших квадратов (использующего квадратичную функцию
ошибки), красным цветом — прямая, построенная с помощью минимизации
функции ошибки, выраженной через функцию Хубера:
Хорошо видно, что при использовании функции Хубера выбросы оказывают
значительно меньшее влияние на результат, и построенная модель оказывается
заметно точнее.
В использованной программе вычисляется полином заданной степени, построенный по набору узлов, которые отмечаются кликами мыши. При вычислении наилучшего полинома используется либо метод наименьших квадратов, при этом минимизируется функция ошибки MSE; либо модель строится путем минимизации функции средней ошибки с использованием функции Хубера (это близко к функции ошибки MAE). Вот исходный код программы на Python'е: "huberRegression.py". Программа использует также модуль "R2Graph.py", архив всех файлов: "huberRegression.zip".
Семинар 8, 15 апреля 2022
Решение задачи линейной регрессии
методами линейного программирования
В задаче линейной регрессии мы строим зависимость между независимой переменной x∈Rn и зависимой переменной y∈R. Зависимость описывается вектором w∈Rn и свободным членом b∈R:

Из-за двух выбросов построенная линия заметно отклоняется от линии, вдоль которой располагаются "регулярные" точки.
Если вместо средней величины квадрата разности минимизировать абсолютную величину разности, то построенная модель будет в значительно меньшей степени зависеть от выбросов. Среднее значение абсолютной величины ошибки обозначается через MAE (Mean Average Error):
Проблемой является то, что функция модуля не дифференцируема в нуле. Это мешает применять алгоритмы минимизации (градиентный спуск, метод сопряженных градиентов и др.), предполагающие, что минимизируемая функция дифференцируема. Ранее было рассмотрено использование функции потерь Хубера вместо модуля, которая является как бы компромиссом между квадратичной функцией потерь (квадрат разности двух величин) и модулем разности. Однако задачу минимизации среднего значения абсолютной величины ошибки можно решить и методами линейного программирования.
Трюк с избавлением от модуля
Приведенная формулировка задачи минимизации не позволяет сразу применить методы линейного программирования из-за использования функции модуля. Однако можно применить следующий трюк. Пусть мы минимизируем сумму модулей некоторых величин |ei|, i=1,…,m. Каждую величину ei, которая может быть положительной и отрицательной, можно представить в виде разности двух положительных величин:
ui + vi → min,
Переформулируем задачу линейной регрессии. Во-первых, можно избавиться от свободного члена b, добавив ко всем объектам x дополнительный признак, тождественно равный единице (т.е. еще одну дополнительную координату к каждому вектору). Вместо исходной линейной модели
Опустим штрихи в обозначениях x', w', чтобы не загромождать запись. Итак, нам надо минимизировать следующую сумму:
ui ≥ 0, vi ≥ 0, i=1,…,m.
ui ≥ 0, vi ≥ 0, i=1,…,m,
∑i(ui + vi) → min
Решение задачи линейного программирования в Python'е: модуль pulp
В Питоне для решения задачи линейного программирования (а также целочисленного программирования) следует использовать модуль pulp. В начале программы можно импортировать все определения из модуля:
from pulp import *
Способ записи формулировки задачи очень простой. Сначала мы создаем объект, отвечающий за решение нашей задачи:
problem = LpProblem("Regression", LpMinimize)
Создан объект типа "Задача линейного программирования"
(LpProblem) с именем "Regression" для решения задачи минимизации.
Затем надо определить 3 вещи.
-
Набор переменных, описывающих нашу задачу. По умолчанию,
переменная принимает вещественное значение, но можно задавать
также целочисленные и логические переменные. Переменная может быть
свободной, т.е. принимать любые значения без ограничений;
можно также задавать нижнюю или верхнюю границу изменения переменной
или обе границы сразу. Примеры описаний отдельных переменных:
x = LpVariable("x") # Свободная вещественная переменная x y = LpVariable("y", 0) # Неотрицательная вещ. переменная y >= 0 v = LpVariable("v", lowBound=0) # Неотрицательная вещ. переменная v >= 0 z = LpVariable("z", upBound=0) # Вещ. переменная z <= 0 t = LpVariable("t", 0, 3) # Вещ. переменная 0 <= t <= 3 i = LpVariable("i", 0, cat="Integer") # Целочисленная переменная i >= 0Можно описать сразу целый список (или словарь) переменных:n = 3 x = LpVariable.dicts("x", range(n), lowBound=0)Описаны неотрицательные вещественные переменные x[0], x[1], x[2] с именами x_0, x_1, x_2. -
Ограничения в форме равенств или неравенств.
Ограничения добавляются к нашему объекту, описывающему задачу,
при помощи операции +=.
Примеры:
problem += 2*x + 3 <= 0 problem += x - 2*y == 1Возможны только три операции сравнения: <=, ==, >= (равенство или нестрогое неравенство).
Для суммирования списка выражений можно использовать функцию lpSum:a = [0.5, -2.7, 1.9] x = LpVariable.dicts("x", range(3), lowBound=0) problem += lpSum([a[i]*x[i] for i in range(3)]) <= 10Здесь мы добавили ограничение0.5*x_0 - 2.7*x_1 + 1.9*x_2 <= 10. -
Целевая функция, которую мы минимизируем или максимизируем.
В отличие от ограничений, целевая функция только одна.
Она также добавляются к объекту, описывающему задачу,
при помощи операции +=.
Запись целевой функции отличается от записи ограничений тем,
что в ней не присутствует операция сравнения.
Пример:
problem += x + y - 2*zВ записи целевой функции тоже можно использовать функцию суммирования lpSum:problem += 0.5*w + lpSum([x[i] for i in range(3)])
Пример решения задачи регрессии методом линейного программирования
Пусть мы имеем набор значения независимой величины x и набор соответствующих измерений зависимой величины y:| x: | -6 | -4 | -3 | -1 | 1 | 2 | 3 | |||||||
| y: | -2 | -1 | 1 | 2 | 2 | 3 | 4 |
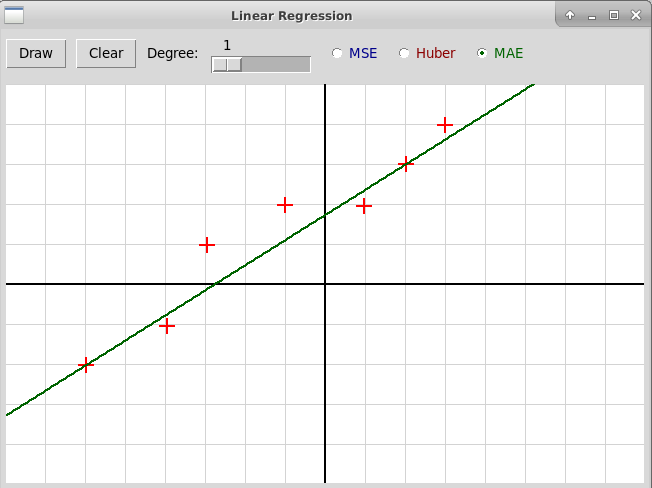
Это можно сделать, используя следующий код на Питоне:
from pulp import *
x = [-6, -4, -3, -1, 1, 2, 3]
y = [-2, -1, 1, 2, 2, 3, 4]
m = len(x)
problem = LpProblem("Regression", LpMinimize)
# Variables:
w = LpVariable.dicts("w", range(2))
u = LpVariable.dicts("u", range(m), lowBound=0)
v = LpVariable.dicts("v", range(m), lowBound=0)
# Constraints:
for i in range(m):
problem += w[0]*x[i] + w[1]*1 - y[i] == u[i] - v[i]
# Objective function:
problem += lpSum([u[i] + v[i] for i in range(m)])
# Solve the problem using the default solver
problem.solve()
# Print the status of solution
print("Status:", LpStatus[problem.status])
# Print the result: w = (w_0, w_1)
print("Regression coefficients:", value(w[0]), value(w[1]))
В результате выполнения этого скрипта печатается результат:
Status: Optimal Regression coefficients: 0.625 1.75Эти параметры соответствуют прямой, изображенной на рисунке выше:
Домашнее задание
Дополнить программу
"huberRegression.py",
которая вычисляет линейную регрессию, используя либо
метод наименьших квадратов (т.е. минимизируя
квадратичную функцию ошибки MSE), либо минимизируя функцию
ошибки, определенную с помощью функции Хубера.
Архив всех файлов программы:
"huberRegression.zip".
В программе надо дополнительно реализовать третий способ
вычисления параметров регрессии, который минимизирует
среднюю величину абсолютной ошибки MAE, используя методы
линейного программирования. Модифицированная программа
должна выглядеть примерно так:

На приведенном скриншоте по заданным узлам
строится прямая, т.е. полином степени 1.
Синим цветом нарисована прямая, построенная методом наименьших
квадратов, красным — с использованием функции Хубера,
зеленым — с помощью минимизации функции MAE
методом линейного программирования.
Можно также построить полином большей степени, например, третьей
(степень полинома задается с помощью слайдера):

Здесь синяя кривая построена методом наименьших
квадратов, зеленая —
методом линейного программирования. Видно, что во втором случае
влияние выбросов на форму кривой значительно меньше.
Красная кривая, построенная с использованием функции Хубера, здесь не
показана, потому что она в данном случае почти совпадает
с зеленой кривой и на картинке две кривые почти полностью
накладываются друг на друга.
Семинар 8, 29 апреля 2022
Метод главных компонент
(Principal Component Analysis, PCA)
В пространстве объектов x = (x1, x2, …, xn) ∈Rn выбирается новая координатная система, обладающая следующими свойствами.
- Начало координат находится в центре тяжести множества точек.
- Координаты точек в новой системе, т.е. новые признаки, не зависят друг от друга (матрица ковариаций диагональная).
- Дисперсии (т.е. разброс точек) по каждой координате убывают в зависимости от номера координаты.
- Это позволяет уменьшить размерность задачи, отбросив несущественные признаки, т.е. последние координаты, разброс точек вдоль которых (дисперсия) невелик.
Этот метод относится к предварительной обработке объектов еще до применения методов машинного обучения (определения параметров линейной регрессии, построения классификатора и т.п.).
Какие могут быть проблемы с данными?
- Всегда хорошо бы данные нормировать — например, чтобы среднее значение векторов xi было бы равно нулю (центрировать данные).
-
Данные могут иметь очень большую размерность не по существу —
например, точки в n-мерном пространстве, представляющие наши объекты,
могут быть расположены на какой-то гиперплоскости (или вблизи
этой гиперплоскости), т.е. реальная размерность наших данных может
быть понижена.
Пример: рассматриваем распознавание рукописных цифр. Каждая цифра — это матрица чисел размера 8x8, т.е. размерность нашего пространства равна 64. Однако ясно, что по существу размерность должна быть меньше хотя бы потому, что пиксели вблизи границ изображения (например, в углах картинки) почти всегда нулевые и не несут никакой информации.
Метод главных компонент
1) центрирует данные, т.е. находит среднюю точку pca.mean_
2) строит ортонормированный базис pca.components_ (это массив из n элементов),
каждый элемент базиса — это вектор нормы 1, все векторы базиса
ортогональны друг другу, и
-
дисперсии проекций векторов xi на векторы базиса
e1, e2, ..., en
убывают (нестрого).
Дисперсия — это мера разброса точекvari = ∑j ( ⟨xj, ei⟩ − (1/n) ∑k⟨xk, ei⟩ )2,
var1 ≥ var2 ≥ ... ≥ varn. - ковариация по разным направлениям равна нулю (мера зависимости двух случайных величин), т.е. точки разбросаны независимо по каждому из направлений ei.
Итак, имеем описания наших объектов в исходной системе координат. В методе главных компонент выбирается новая ортогональная система координат, в которой координаты, начиная с номера k+1, будут очень малы, и их можно вообще не учитывать. Оставшиеся первые k координат называются главными компонентами. Каждая из главных компонент — это некоторая линейная комбинация исходных признаков. Причем все главные компоненты уже не зависят друг от друга (ортогональны).
Пример: в военном деле давно известно, что при стрельбе снаряды рассеиваются по нормальному закону (закону Гаусса), по так называемым эллипсам рассеивания. Полуоси этого эллипса соответствуют главным компонентам.
Если мы рассматриваем случайные точки в n-мерном пространстве, распределенные, скорее всего, по закону, близкому к нормальному распределению, то они тоже находятся внутри n-мерного эллипсоида; полуоси этого эллипсоида и будут главными компонентами.
Если только первые k полуосей этого эллипсоида имеют значительный размер (остальные очень малы), то мы можем взять проекции исходных точек на гиперплоскость, натянутую на первые k полуосей эллипсоида. При этом мы потеряем очень мало информации, поскольку разброс вдоль остальных направлений минимален.
Главные компоненты вычисляются путем приведения матрицы ковариаций к диагональному виду.
В Питоне все это реализовано в модуле
sklearn.decomposition
(предварительная обработка данных, обучение еще без учителя).
Из этого модуля мы импортируем объект PCA (Principal Component Analysis).
Пусть исходные данные нашей задачи представляют собой массив x векторов,
описывающих наши объекты: элемент массива x[i] —
это n-мерный вектор, содержащий
признаки (features) i-го объекта.
Для того, чтобы обработать исходные данные x,
мы вызываем метод fit объекта типа PCA:
from sklearn.decomposition import PCA
. . .
pca = PCA() # Не указываем количество компонент, их число будет равно
# числу признаков
pca = PCA(n_components = 3) # Выделяются всего 3 первых главных компоненты
pca.fit(x) # Вычисляем новую систему координат, связанную
# с главными компонентами
x_tranformed = pca.transform(x) # Вычисляем координаты объектов в
# новой системе координат, связанной с
# заданным числом главных компонент.
Размерность векторов из x_transformed равна числу главных компонент,
указанных в конструкторе объекта pca.
Давайте напишем простую программу в Jupyter-Lab, которая иллюстрирует метод главных компонент в 2-мерном случае.
Попробуем сгенерировать случайный набор данных (точки на плоскости), применить для него метод главных компонент и нарисовать новую систему координат, построенную с помощью метода главных компонент. Исходные точки изображены синим цветом. Проекции исходных точек на первую главную компоненту изображены красным цветом (используется полупрозрачный режим рисования). Длины базисных векторов, соответствующих главным компонентам, равны квадратному корню из дисперсии по соответствующему направлению.
import numpy as np
import random
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
%matplotlib inline
# Generate a random data
origin = np.array([0., 1.])
v = np.array([2., 1.])
v /= np.linalg.norm(v) # make norm(v) = 1.
n = np.array([-v[1], v[0]])
m = 50
x = [
origin + v * random.normalvariate(3., 4.) +
n * random.normalvariate(0., 2.)
for i in range(m)
]
x = np.array([[xx[0], xx[1]] for xx in x])
plt.axes(aspect="equal")
# plt.xlim(min(x[:, 0])-1., max(x[:, 0])+1)
# plt.ylim(min(x[:, 1])-1., max(x[:, 1])+1)
# plt.grid()
plt.scatter(x[:, 0], x[:, 1], color="blue")
pca = PCA()
pca.fit(x)
e0 = pca.components_[0]
variance0 = pca.explained_variance_[0]
e1 = pca.components_[1]
variance1 = pca.explained_variance_[1]
center = pca.mean_
pca = PCA(n_components = 1)
pca.fit(x)
x_tranformed = pca.transform(x)
x_reduced = pca.inverse_transform(x_tranformed)
plt.scatter(x_reduced[:, 0], x_reduced[:, 1], color="red", alpha=0.3)
plt.arrow(
center[0], center[1],
e0[0] * variance0**0.5, e0[1] * variance0**0.5,
color="black",
width=0.1
)
plt.arrow(
center[0], center[1],
e1[0] * variance1**0.5, e1[1] * variance1**0.5,
color="black",
# length_includes_head=True,
width=0.1
)
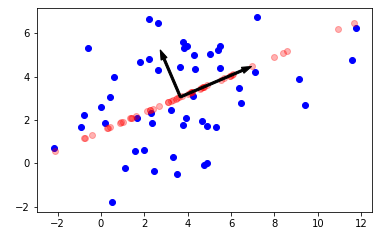
В следующем примере мы рассматриваем базу NIST рукописных цифр (это матрицы размера 8x8, размерность объектов 64). Применяя метод главных компонент, мы оставляем сначала только две первых компоненты, затем 3. Полученные точки изображаются разными цветами, соответствующими десяти разным цифрам, в первом случае на плоскости, во втором случае — в трехмерной проекции.
import numpy as np
import random
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
%matplotlib inline
from sklearn.datasets import load_digits
digits = load_digits()
print(digits.data.shape)
# plt.imshow(digits.data[1001].reshape((-1, 8)), cmap='gray')
pca = PCA()
x = digits.data
pca.fit(x)
# print("Variance:")
# print(pca.explained_variance_)
# print("Variance ratio:")
# print(pca.explained_variance_ratio_)
# xx = np.linspace(0, 64, 64)
# plt.plot(xx, np.cumsum(pca.explained_variance_ratio_))
variance_ratio = 0.8
pca = PCA(variance_ratio) # 80% of total variance must be preserve
pca.fit(x)
print(
"for variance ratio ", variance_ratio, " we need",
len(pca.components_), "components"
)
pca = PCA(n_components = 2)
x = digits.data
pca.fit(x)
x_transformed = pca.transform(x)
plt.scatter(
x_transformed[:, 0],
x_transformed[:, 1],
c = digits.target,
alpha = 0.5,
cmap=plt.cm.get_cmap('tab10')
)
plt.xlabel('component 1')
plt.ylabel('component 2')
plt.colorbar();
# print(digits.target[111])
# plt.imshow(digits.data[111].reshape((-1, 8)), cmap='gray')
pca = PCA(n_components = 3)
x = digits.data
pca.fit(x)
x_transformed = pca.transform(x)
print("Variance_ration:", pca.explained_variance_ratio_)
print("Total variance ratio:", sum(pca.explained_variance_ratio_))
fig = plt.figure()
# ax = fig.add_subplot(111, projection='3d')
ax = plt.axes(projection='3d')
p = ax.scatter3D(
x_transformed[:, 0],
x_transformed[:, 1],
x_transformed[:, 2],
c = digits.target,
alpha = 0.5,
cmap=plt.cm.get_cmap('tab10')
);
fig.colorbar(p)
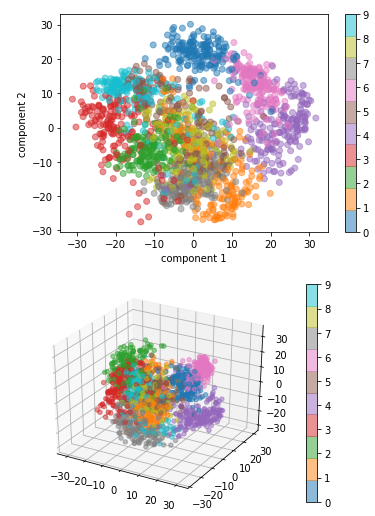
Классификация рукписных цифр с использованием метода главных компонент
Объекты, представляющие рукописные цифры, являются матрицами размера 8x8, т.е. размерность пространства объектов равна 64, по количеству пикелей изображения. Между тем значительная часть этих пикселей не имеет значения при классификации — напримерЁ пиксели в углах изображения. Метод главных компонент позволяет значительно сократить размерность пространства объектов, сохранив при этом точность классификации. Ниже приведена программа на Питоне "digitSvmPcaClassification.py", которая вычисляет точность классификации при заданном числе главных компонент, существенно меньшем, чем 64.
import numpy as np
import random
from sklearn.decomposition import PCA
from sklearn.datasets import load_digits
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
digits = load_digits()
m = len(digits.data)
x = digits.data
y = digits.target
num_components = 8
pca = PCA(n_components = num_components)
pca.fit(x)
x_transformed = pca.transform(x)
m_train = int(m*3/4)
m_test = m - m_train
print("Number of digit images:", m)
print("Train part:", m_train, " Test part:", m_test)
C = 4.0
kernel = "rbf"
num_repeats = 10
print("Number of repetitions:", num_repeats)
mean_accuracy = 0.
for i in range(num_repeats):
x_train, x_test, y_train, y_test = train_test_split(
x_transformed, y, test_size=1/4, shuffle=True, stratify=y
)
# model = SVC(C=C, kernel=kernel, degree=degree, coef0=coef0)
model = SVC(C=C, kernel=kernel)
model.fit(x_train, y_train)
y_predicted = model.predict(x_test)
accuracy = accuracy_score(y_true=y_test, y_pred=y_predicted)
mean_accuracy += accuracy
mean_accuracy /= num_repeats
print("Mean accuracy of classification:", mean_accuracy)
Вот результат работы программы:
/home/vvb/MasterAI>python3 digitSvmPcaClassification.py
Number of digit images: 1797
Train part: 1347
Test part: 450
Number of repetitions: 10
Mean accuracy of classification: 0.9693333333333335
Как мы видим, точность классификации при только 8-ми оставленных
главных компонентах составляет почти 97%.
Осенний семестр 2021 г.
Журнал группы магистратуры 1 курса, осенний семестр 2021 г.:
Семинары, записи на "виртуальной доске"
Материалы к семинарам
- Семинар 5.10.2021
- Семинар 14.10.2021
- Семинар 19.10.2021
- Семинар 26.10.2021
- Семинар 2.11.2021
- Семинар 9.11.2021
Семинар 1, 5 октября 2021
Содержание: основы языка Python3, базовые типы данных и операции над ними. Среда разработки Jupyter-Lab. Функции. Использование программы как скрипта и как модуля. Разбор способа решения кубического уравнения. Описание см. здесь: Решение кубического уравнения.
Домашнее задание
Написать на Python'е функцию, решающую кубическое уравнение.
Семинар 2, 14 октября 2021
Содержание: конструкции цикла и условного оператора в Питоне. Примеры некоторых алгоритмов теории чисел: наибольший общий делитель целых чисел, быстрое возведение в степень по модулю m. Наивные алгоритмы проверки простоты и факторизации (разложения на множители) целого числа; ρ-алгоритм факторизации Полларда.
Все разобранные алгоритмы содержатся в файле "numTheory.py".
С теорией можно познакомиться здесь:
Кодирование с открытым
ключом и элементы теории чисел.
Презентация на эту тему:
Теория чисел
в криптографии.
Домашнее задание
Используя функцию pollardRhoFactor(m, maxSteps=10000000), реализовать разложение большого числа на множители. Функция должна возвращать список множителей, не обязательно простых. Пример:>>> m = 123456768901234567890123 >>> pollardRhoFactor(m) 3 >>> m //= 3 >>> pollardRhoFactor(m) 95194207 >>> m //= 95194207 >>> pollardRhoFactor(m) 1 >>> m 432297905485063 >>> isPrime(m) TrueТаким образом, для числа m = 123456768901234567890123 функция должна возвращать список
[3, 95194207, 432297905485063]
(Не требуется, чтобы множители были бы обязательно простыми;
алгоритм разложения заканчивается, когда функция pollardRhoFactor(m)
не может найти нетривиальный делитель числа m.)
Семинар 3, 19 октября 2021
Содержание: списки в Питоне и методы списков. Особенности Питона как объектно-ориентированного языка: переменные содержат объектные ссылки, а не сами объекты. Типичная ошибка при работе со списками в Питоне: копирование объектной ссылки вместо получения копии списка на примере задачи о счастливых билетах. Номер билета счастливый, если сумма цифр его первой половины совпадает с суммой цифр второй половины.
Следующая функция luckyTickets(n) возвращает список счастливых номеров билетов для номеров из n цифр, где n четное. Номер билета представляется списком длины n, содержащим числа от 0 до 9 (цифры номера).
def nextTicket(t):
n = len(t)
pos = n - 1
while pos >= 0:
if t[pos] < 9:
t[pos] += 1
return True
t[pos] = 0
pos -= 1
return False
def isLucky(t):
n = len(t)
k = n // 2
s0 = 0
for i in range(0, k):
s0 += t[i]
s1 = 0
for i in range(k, n):
s1 += t[i]
return (s0 == s1)
def luckyTickets(n):
assert n > 0 and n%2 == 0
t = [0]*n
s = []
while True:
if isLucky(t):
# s.append(t) ERROR!
s.append(t.copy()) # Correction: save a copy of mutable object
if not nextTicket(t):
break
return s
Алгоритмы теории чисел (продолжение предыдущего семинара)
Тесты простоты. Малая теорема Ферма как необходимое
условие простоты числа m:
bm-1 ≡ 1 (mod m)
но 341 = 31⋅11 не является простым числом.
Следующая теорема дает описание кармайкловых чисел.
1) m свободно от квадратов, т.е. m = p1p2... pk, где pi — разные простые числа;
2) k ≥ 3;
3) для всякого i=1,2,..., k число pi - 1 делит m - 1.
Пример: число 561 кармайклово, т.к. 561 = 3⋅11⋅17 и (3-1)|560, (11-1)|560, (17-1)|560.
Вероятностный тест простоты Миллера-Рабина
Хотя Малую теорему Ферма нельзя использовать в качестве теста простоты ввиду существования кармайкловых чисел, ее можно немного подправить, чтобы получить вероятностный тест простоты. Он, используя датчик случайных чисел, для любого числа m выдает один из двух ответов:
2) не знаю.
Домашнее задание
- Написать функцию, которая возвращает число счастливых билетов длины n, где n — четное число. Функция должна работать по крайней мере для n≤16. Отметим, что функция не должна перебирать все номера и определять среди них счастливые, потому что такой перебор для n>8 уже невозможен (к примеру, число счастливых билетов длины 16 равно 343900019857310). Требуется придумать какой-нибудь более-менее нетривиальный алгоритм для решения этой задачи.
-
Во второй задаче 2 варианта. Студенты с нечетными номерами по
журналу решают перый вариант, с четными — второй.
- Написать функцию carmichaelNumbers(n), которая возвращает список всех кармайкловых чисел, меньших n.
-
Написать функцию generatePrime(n), которая
возвращает случайное простое число p,
в двоичной записи которого ровно n цифр:
2n-1 ≤ p < 2n.
Функция должна работать по крайней мере для n=1000, поэтому для проверки простоты числа следует воспользоваться тестом простоты Миллера-Рабина.
Семинар 4, 26 октября 2021
Содержание: разбор домашнего задания предыдущего семинара (на уровне идеи алгоритма). Простой алгоритм подсчета числа счастливых билетов длины n: перебираем все номера половинной длины k = n/2. Используем массив comb размера 9*k+1, элемент этого массива comb[s] содержит число комбинаций цифр длины k, сумма цифр которых равна s. Тогда искомое число счастливых билетов равно сумме квадратов элементов массива comb. Вот псевдокод этого адгоритма:
функция numberOfLuckyTickets(n)
k = n/2
comb = целочисленный массив размера 9*k + 1,
инициализированный нулевыми значениями
# comb[s] = число комбинаций цифр длины k с суммой s.
цикл для всех комбинаций t цифр длины k
| s = сумма цифр(t)
| comb[s] += 1
конец цикла
res = 0
цикл для всех элементов x массива comb
| res += x*x
конец цикла
ответ = res
конец функции
Здесь в первом цикле перебираются все номера половинной длины, например,
для n=10 тело цикла выполняется 105 раз. Можно очень
существенно ускорить перебор, рассматривая только всевозможные
упорядоченные наборы из цифр длины k. Любой такой набор задается
неубывающим списком цифр длины k. Например, для k=5 возможны
следующие наборы:
[0, 0, 2, 2, 8], [1, 2, 3, 3, 3], [5, 5, 5, 9, 9]
Нетрудно подсчитать количество разных комбинаций цифр для заданного
набора. Например, число комбинаций для набора [0, 0, 2, 2, 8] равно
5!/(2!⋅2!)=30, поскольку всего имеется 5! перестановок цифр набора,
при этом в наборе цифры 0 и 2 повторяются дважды каждая, поэтому надо
разделить общее число перестановок на произведение 2!⋅2!. Для
набора [5, 5, 5, 9, 9] число комбинаций равно 5!/(3!⋅2!)=10,
поскольку цифра 5 в нем повторяется 3 раза, а цифра 9 — 2 раза.
При этом, например, количество неубывающих списков цифр длины 5
равно 2002, что существенно меньше, чем число 100000 всех неупорядоченных
комбинаций из цифр длины 5. Даже для k=10 число неубывающих
списков цифр равно 92378, что сравнительно невелико; это позволяет подсчитать
число счастливых билетов длины n=2k=20,
оно равно 3081918923741896840.
Чтобы перебрать в цикле все упорядоченные наборы цифр длины k, достаточно по упорядоченному набору уметь вычислять следующий набор в лексикографическом порядке. (При этом мы не создаем новый список, а только меняем элементы текущего списка.) Функция возвращает True, если это удается сделать, и False, если текущий набор уже максимальный относительно лексикографического порядка:
def nextOrderedList(s):
k = len(s)
i = k - 1
while i >= 0 and s[i] == 9:
i -= 1
if i < 0:
return False
d = s[i] + 1
while i < k:
s[i] = d
i += 1
return True
Для примера, применим эту функцию дважды к спискуs = [3, 4, 4, 5, 9, 9, 9]:
>>> s = [3, 4, 4, 5, 9, 9, 9]
>>> nextOrderedList(s)
True
>>> s
[3, 4, 4, 6, 6, 6, 6]
>>> nextOrderedList(s)
True
>>> s
[3, 4, 4, 6, 6, 6, 7]
Работа со списками
В Питоне есть удобный способ задания списка: list comprehension, на русский язык можно перевести как "умное задание списка" или "математическое задание списка". Скорее всего, в Питоне он появился под влиянием функциональных языков, в которых он очень популярен.
Как, например, в математике задать множество чисел в диапазоне от 1 до m, обратимых в кольце Zm (т.е. взаимно простых с m)? Можно использовать запись вроде следующей:
>>> from math import gcd
>>> m = 15
>>> S = [ x for x in range(1, m) if gcd(x, m) == 1 ]
>>> S
[1, 2, 4, 7, 8, 11, 13, 14]
При использовании list comprehension мы сначала задаем выражение,
зависящее от одного или нескольких переменных, затем с помощью конструкции
for определяем диапазон изменения каждой переменной, наконец, последним
элементом является фильтр, т.е. логическое выражение, отбирающее комбинации,
для которых оно истино. Еще примеры:
-
квадраты первых 20 натуральных чисел — список пар вида
(x, x2):
>>> [ (x, x**2) for x in range(1, 21) ] [(1, 1), (2, 4), (3, 9), (4, 16), (5, 25), (6, 36), (7, 49), (8, 64), (9, 81), (10, 100), (11, 121), (12, 144), (13, 169), (14, 196), (15, 225), (16, 256), (17, 289), (18, 324), (19, 361), (20, 400)]
-
пифагоровы тройки в интервале от 1 до 100. Тройка натуральных чисел
(a, b, c) называется пифагоровой. если
a≤b, gcd(a, b) = 1 и a2 + b2 = c2(нам всем хорошо знакома такая тройка для египетского треугольника 3, 4, 5). Вот как список этих троек задается в Питоне с помощью list comprehension:
>>> [(a, b, c) for a in range(1, 101) ... for b in range(a, 101) ... for c in range(b, 101) ... if gcd(a, b) == 1 and a**2 + b**2 == c**2] [(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12, 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77, 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)]
Алгоритм факторизации "Колесо со спицами"
Конструкцию list comprehension удобно использовать в несложном алгоритме факторизации "Колесо со спицами". Пусть m = 2⋅3⋅5 = 30. Выпишем все числа от 1 до 30, которые не делятся на 2, 3, 5:
>>> [ d for d in range(1, 30) if gcd(d, 30) == 1 ]
[1, 7, 11, 13, 17, 19, 23, 29]
Самый простой алгоритм разложения целого числа на множители состоит в том, что мы сначала проверяем, делится ли число на 2; если нет, то мы пытаемся делить число на все пробные нечетные делители.
Идея "Колеса со спицами" сходная: сначала делим число на 2, 3, 5. Если оно не делится ни на одно из них, то затем делим число на все пробные делители, не кратные 2, 3, 5. Это числа вида
d ∈ [1, 7, 11, 13, 17, 19, 23, 29]
| 2, | 3, | 5, | |||||
| 7, | 11, | 13, | 17, | 19, | 23, | 29, | |
| 31, | 37, | 41, | 43, | 47, | 49, | 53, | 59, |
| 61, | 67, | 71, | 73, | 77, | 79, | 83, | 89, |
Домашнее задание
В задании 2 варианта, оба связаны с алгоритмом "Колесо со спицами".
-
Реализовать алгоритм проверки простоты числа типа "Колесо со спицами"
с длиной обода
m = 2⋅3⋅5⋅7⋅11⋅13⋅17⋅19 = 9699690.Тогда список обратимых элементов кольца вычетов Zm
[ d for d in range(1, m) if gcd(d, m) == 1 ]состоит из 1658880 элементов (это значение функции Эйлера ϕ(m)). - Та же задача для разложения числа на множители.
Семинар 5, 2 ноября 2021
Содержание: в прошлый раз было рассмотрено задание списков в Python с помощью list comprehension (можно перевести как умное, или математическое задание списков). На самом деле, конструкция list comprehension, а также конструкция цикла for реализуется с помощью итераторов. Итератор — это объект, с помощью которого мы перебираем элементы некоторого набора данных — диапазона чисел, списка, множества, словаря и т.п. У объекта it такого типа должно быть два метода:
- метод __iter__(self), который вызывается с помощью функции iter(it), возвращает ссылку на сам объект it;
- метод __next__(self) вызывается с помощью функции next(it). Он возвращает объект, на который (как бы) ссылается итератор, при этом сам итератор переходит к следующему объекту. Если итератор уже переместился за конец структуры данных, то при выполнении next(it) произойдет исключение типа StopIteration.
Конструкция
for x in s:
action(x)
это синтаксический сахар для
i = iter(s)
while True:
try:
x = next(i)
action(x)
except StopIteration:
break
В Python'е можно честно написать класс, представляющий итератор нужного типа, в этом классе надо реализовать два метода __iter__(self) и __next__(self); конечно, нужно реализовать также конструктор и другие необходимые методы. Однако в Python'е есть еще два упрощенных способа создания итераторов. Это
2) генераторные выражения (generator expressions).
Генератор (или генераторная функция) — это функция, в которой значения возвращаются не с помощью ключевого слова return, а с помощью yield. В процессе работы такая функция генерирует последовательность значений, по которой и осуществляется итерация. При использовании генераторной функции в цикле for автоматически создается генераторный объект, реализующий интерфейс итератора. В нем запоминается фрейм локальных переменных генераторной функции и точка, в которой она прервала свое выполнение. При выполнении метода next генератора генераторная функция возобновляет свою работу с прерванного места до выполнения очередного оператора yield. Значение, выдаваемое по yield, используется в качестве очередного значения, по которым ведется итерация. Когда функция заканчивает работу, генератор возбуждает исключение типа StopIteration.
Пример генератора: перебираем все целочисленные точки плоскости в первом квадранте, у которых сумма координат не превышает maxNum.
def nodes(maxNum):
n = 0
while n <= maxNum:
x = n; y = 0
while x >= 0:
yield (x, y)
x -= 1; y += 1
n += 1
Пример использования этого генератора:
>>> for p in nodes(3):
... print(p)
...
(0, 0)
(1, 0)
(0, 1)
(2, 0)
(1, 1)
(0, 2)
(3, 0)
(2, 1)
(1, 2)
(0, 3)
С помощью этого генератора можно найти
хорошее приближение числа pi в виде целочисленной дроби:
ищем приближение с ошибкой, не превышающей единицы, деленной
на квадрат знаменателя дроби.
from math import pi
prec = 1e30 # infinity
m = (3, 1)
for p in nodes(1000):
if p[1] == 0:
continue
d = abs(pi - p[0]/p[1])
if d < 1/(p[1]**2) and d < prec:
m = p
prec = d
print(m)
print("pi is approximated as", m[0], "/", m[1])
Вот результат выполнения этой программы:
(3, 1)
(19, 6)
(22, 7)
(333, 106)
(355, 113)
pi is approximated as 355 / 113
Генераторное выражение (generator expression) — это такое же выражение, которое используется в list comprehension, но в круглых скобках. Пример:
s = (d for d in range(1, 30) if gcd(d, 30) == 1)
Это генераторное выражение эквивалентно генераторной функции:
def f():
for d in range(1, 30):
if gcd(d, 30) == 1:
yield d
Домашнее задание
Задача:
написать генератор для всех перестановок порядка n.
Перестановки должны перебираться в лексикографическом порядке.
[1, 2, 3]
[1, 3, 2]
[2, 1, 3]
[2, 3, 1]
[3, 1, 2]
[3, 2, 1]
Замечание: удобно реализовать вспомогательную функцию nextPermutation(s), на вход подается список чисел, на выходе этот список изменяется. Функция возвращает True, если перестановка была не последней, и False, если следующей перестановки нет. Используется следующий алгоритм:
6, 3, 1, 2, 10, 4, 9, 12, 11, 8, 7, 5
2) для предшествующего к ней элемента x
(в примере x=9, выделен синим)
находим минимальный элемент y возрастающей последовательности,
больший x (в примере
y=11, отмечен подчеркиванием);
6, 3, 1, 2, 10, 4, 9, 12, 11, 8, 7, 5
3) меняем местами элементы x и y и затем упорядочиваем
элементы в конце перестановки, следующие за элементом y
(для этого используем метод sort для отрезка списка, следующего за y).
6, 3, 1, 2, 10, 4, 11, 5, 7, 8, 9, 12
Необязательная задача
Написать две функции:
2) обратная функция: по списку независимых циклов получить перестановку.
Семинар 6, 9 ноября 2021
Содержание: обработка текстов. Элементы теории формальных языков и грамматик. контекстно-свободные и регулярные (автоматные) языки. Использование регулярных выражений (модуль re, от Regular Expressions) для поиска и выделения фрагментов текста по заданному образцу.
Коротко о теории формальных языков
Хомский предложил определение формальных грамматик и языков, задаваемых ими.
S ∈ N — начальный нетерминал
Вывод в данной грамматике начинается с метасимвола S и состоит в последовательности замен по правилам грамматики. Вывод заканчивается, когда в выводимой цепочки не останется метасимволов, т.е. цепочка будет состоять из одних только терминалов (отсюда и такое название — на терминалах заканчивается процесс вывода). Язык, задаваемый формальной грамматикой, состоит из всех терминальных цепочек, выводимых из начального метасимвола грамматики.
Для упрощения обозначений традиционно метасимволы изображаются большими латинскими буквами, терминалы — маленькими буками из начала алфавита (a, b, c, d, e, ...); маленькими буквами из конца алфавита обозначаются любые цепочки из терминалов и нетерминалов (u, v, x, y, z, ...).
Задача: текстовая строка содержит запись формулы, например:
Для решения подобных задач мы сначала определим язык арифметических формул, задав его с помощью контекстно-свободной грамматики.
F → a | F + F | F - F | F * F | F / F | (F)
В этой грамматике выводимы арифметические формулы, где вместо констант и переменных используется буква a, например,
S => F $ => F + F $ => a + F $ => a + F/F $ => a + (F)/F $ =>
=> a + (F*F)/F $ => a + (a*F)/F $ => a + (a*a)/F $ =>
=> a + (a*a)/(F) => a + (a*a)/(F - F) $ =>
=> a + (a*a)/(a - F) $ => a + (a*a)/(a - a) $
Вывод называется левым, если замены всегда применяется к самому левому
нетерминалу выводимой цепочки. Соответственно вывод правый, если замены
применяются к самому правому нетерминалу. Выше приведен пример левого вывода.
Контекстно-свободная грамматика называется однозначной, если любая выводимая цепочка имеет только один левый вывод, или, что эквивалентно, только один правый вывод, или только одно синтаксическое дерево вывода. Приведенная выше грамматика не является однозначной: например, цепочка
a + a*a $
имеет два разных левых вывода и два разных синтаксических дерева
вывода:
S S
/ \ / \
F $ F $
/|\ /|\
F + F F * F
| /|\ /|\ |
a F * F F + F a
| | | |
a a a a
Здесь левое дерево соответствует трактовке формулы как суммы
a и произведения a*a, что соответствует нашим представлениям о том,
что операция умножения имеет более высокий приоритет. Но второе дерево
трактует ту же самую формулу как произведение суммы a+a на a;
это возможно, поскольку наша грамматика плохая, она никак не учитывает
приоритеты операций и делает возможной разные трактовки одной и той
же формулы.
Переделаем эту грамматику так, чтобы она стала однозначной, введя дополнительные метасимволы T и M для обозначения терма и множителя. Формула в этом случае представляется как сумма или разность нескольких термов, а терм — как произведение или частное нескольких множителей. Множитель — это либо элементарная формула (буква a в нашем случае) или любая формула, взятая в круглые скобки:
S → F $
F → T | F + T | F - T
T → M | T * M | T / M
M → a | ( F )
. . . продолжение следует . . .
Проект "Рисование графика функции"
Проект включает 3 файла:
"scanner.py",
"exprParser.py",
"plotter.py".
Архив всех файлов проекта:
"plotter.zip".
Пример выполнения программы:
/home/vvb/MasterAI>python3 plotter.py Input a function: 4*sin(3*x)/(1 + x*x)

Домашнее задание
Требуется внести следующие изменения в проект "plotter":- добавить унарный минус в грамматику (операция изменения знака);
- добавить константы pi, e;
- добавить операцию возведения в степень, которая обозначается либо как в Питоне **, либо как в математике и в SageMath "^": например, квадрат синуса от х записывается как sin(x)^2 (этот пункт требует изменений и в сканере, и в парсере).