 Информатика, численные методы и программирование
Информатика, численные методы и программирование
 Информатика, численные методы и программирование
Информатика, численные методы и программирование
Зачет в семестре и его оценка ставится
как результат решения задач по указанным темам.
О проблемах сообщайте по электронной почте:
vladibor2016 (собака) yandex.ru
Тексты лекций на "виртуальной доске", прочитанных в прошлые годы (2021-22)
Enter an integer constant n:
123456789012345678901234567
Enter a digit d:
7
n*d:
864197523086419752308641969
Enter an integer constant n:
123456789012345678901234567
n/2:
61728394506172839450617283
В первой задаче:
void multiply(
const char* n,
int d,
char* result
);
Отметим, что массив result имеет длину на 1
больше, чем массив n (если результат умножения имеет
такое же число цифр, как у числа n, то мы
дополняем запись результата пробелом в начале строки).
Прототип функции во второй задаче:
void divideBy2(
const char* n,
char* result
);
Здесь изначально входной и выходной массивы имеют
одинаковую длину, реальное число цифр строки-результата
может быть таким же, как у входной строки, или на
единицу меньшим (можно не убирать первый незначащий
ноль, тогда длины обеих строк будут одинаковыми:
например, 123/2=062).
Указания к обеим задачам: фактически надо реализовать школьные алгоримы умножения и деления чисел в столбик. В первой задаче (умножение) надо вычислять цифры результата, начиная с конца, при этом учитывая перенос из предыдущего разряда. Во второй задаче цифры результата вычисляются слева направо (в естественном порядке), при этом мы учитываем остаток 0 или 1 от деления на 2 при вычислении цифры предыдущего разряда. Пусть, например, мы делим число 385 на 2, первая цифра частного будет 3/2=1 и остаток 1; при вычислении второй цифры частного мы предыдущий остаток умножаем на 10 и прибавляем вторую цифру делимого 8, получаем 18, делим это число на 2 и получаем вторую цифру частного (1·10+8)/2=9 и остаток 0; третья цифра частного получается как (0·10+5)/2=2, остаток 1. В результате получаем 192 и 1 в остатке.
В основной функции main мы только вводим текстовую запись исходного числа n, цифру d для первого варианта, вызываем функцию multiply или divideBy2 и печатаем ответ. Содержательная часть алгоритма выполняется внутри функции. Начало программы (без функции, которую нужно реализовать самостоятельно) выглядит так, для примера мы рассматриваем первый вариант:
#include <iostream>
#include <cctype>
#include <cstring>
using namespace std;
void multiply(
const char* n,
int d,
char* result
);
int main() {
char n[255];
int d;
char result[256];
cout << "Enter an integer constant n:" << endl;
cin.getline(n, 254);
if (!cin.good())
return (-1); // Error input
cout << "Enter a digit d:" << endl;
cin >> d;
if (!cin.good() || d < 0 || d > 9) {
cout << "Incorrect digit." << endl;
return (-1);
}
multiply(n, d, result);
cout << "n*d:" << endl
<< result << endl;
return 0;
}
void multiply(
const char* n,
int d,
char* result
) {
// to do...
}
По этой теме надо решить одну задачу. Всего вариантов 6, студент должен выбрать вариант, номер которого дает при делении на 6 такой же остаток, как и номер студента по журналу. Например, студент с номером 8 по журналу выбирает вариант 2, студент с номером 12 — вариант 6.
Примеры решения задач по этой теме
В 2022 учебном году (осенний семестр) это последняя задача для зачета.
Программа приведения матрицы к ступенчатому виду:
"matrix.cpp".
В этой программе матрица считывается из файла "input.txt",
результат, т.е. матрица, приведенная к ступенчатому виду,
записывается в файл "output.txt". Формат файла:
сначала записываются два числа m и n —
число строк и число столбцов матрицы;
затем записываются элементы матрицы по строкам,
сначала элементы строки с индексом 0,
затем элементы строки с индексом 1, последней идет строка с индексом
m-1.
p(xi) = yi, i=0, 1, ..., n
Для нахождение интерполяционного полинома следует использовать решение линейной системы с матрицей Вандермонда:
1, x0, x02,
x03, ...,
x0n
| y0
1, x1, x12,
x13, ...,
x1n
| y1
1, x2, x22,
x23, ...,
x2n
| y2
. . .
1, xn,
xn2,
xn3, ...,
xnn
| yn
p(x) =
a0 +
a1(x-x0) +
a2(x-x0)(x-x1) +
a3(x-x0)(x-x1)(x-x2) +
. . .
+ an(x-x0)(x-x1)(x-x2)...(x-xn-1)
-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5.
Результаты надо записать в файл в следующем формате: файл должен содержать ровно 11 строк видаx p(x)
(пара чисел), где x последовательно принимает значения -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5.Студент должен решить одну задачу, номер которой совпадает по модулю 3 с его номером по журналу.
Тексты прочитанных лекций на "виртуальной доске"
(группа 102, весенний семестр 2021-22 учебного года).
Реализация метода Гаусса:
"matrix.cpp".
Задачи
по теме "Метод Гаусса".
Лекция Алгоритмы сортировки (презентация)
Нужно решить одну задачу, номер которой совпадает по модулю 3 с номером студента в журнале. В качестве примера можно использовать файл tstSort0.cpp, содержащий функции генерации случайных массивов и их печати, а также прототипы функций сортировки разными методами (реализация дана только для функций bubbleSort и insertionSort, реализации остальных оставлены в качестве задач).
void heapSort(
double *a, // Pointer to the beginning of array
int n // Size of array
);
void mergeSortRecursive(
double *a, // Beginning of array
int n, // Size of array
double* tmpMemory = nullptr // Temporary memory to use
);
void mergeSortBottomTop(
double *a, // Beginning of array
int n, // Size of array
double* tmpMemory = nullptr // Temporary memory to use
);
В задачах интегрируемая функция задается непосредственно в тексте программы, например
double f(double); // Прототип функции
. . .
double f(double x) { // Определение функции
return sin(x);
}
Функция, вычисляющая определенный интеграл по отрезку,
должна иметь следующий прототип:
double integral(
double (*f)(double), // Интегрируемая функция
double a, double b, // Отрезок интегрирования
double h = 0.001 // Приблизительный шаг интегрирования
);
Студенты с нечетными номерами по журналу решают первую задачу,
с четными — вторую.
В качестве образца дается программа, вычисляющая (грубо!) интеграл с помощью формулы прямоугольников: "integral.cpp".
Рассмотренные выше задачи на вычисление замечательных точек треугольника можно оформить в виде графических приложений. Для этого мы используем Qt — самую лучшую графическую среду для разработки оконных приложений. Qt включает оболочку QtCreator и библиотеку классов. Достоинства Qt:
Студент должен сделать задачу, номер которой совпадает по модулю 4 с его номером по журналу.
Если не удается установить Qt и qtcreator, то в крайнем случае можно оформить решения этих задач как консольные программы. Программа должна напечатать приглашение на ввод вершин треугольника, ввести три точки, вычислить соответствующую замечательную точку треугольника и напечатать ее. Задача обязательно должна использовать классы R2Point и R2Vector, подключая заголовочный файл "R2Graph.h". Кроме того, в тексте программы обязательно должна быть функция, вычисляющая соответствующую точку, которой передаются вершины треугольника либо как 3 объекта, либо как массив из трех объектов. Например, для точки Жергона должна быть функция с прототипом
R2Point gergonnePoint(
const R2Point& a, const R2Point& b, const R2Point& b
);
или
R2Point gergonnePoint(
const R2Point* vertices
);
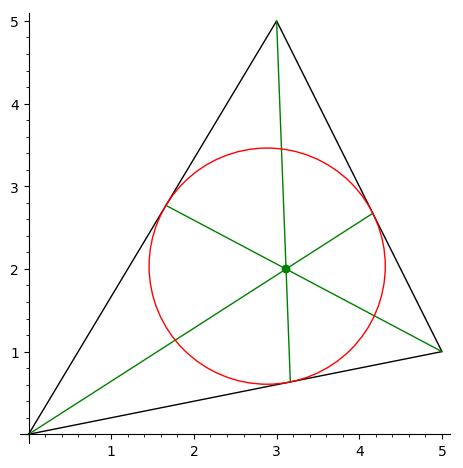
Пример консольного приложения, вычисляющего окружность, вписанную в треугольник (вычисляются ее центр и радиус): "inCircle.cpp". Вершины треугольника вводятся с клавиатуры, результат выводится в выходной поток.
В текущую директорию надо переписать файлы "R2Graph.h" и "R2Graph.сpp", содержащие описание и реализацию классов R2Vector и R2Point, а также функций, использующих классы R2Vector и R2Point (например, найти пересечение двух прямых, каждая прямая задается точкой и направляющим вектором). При компиляции проекта надо подключить также файл "R2Graph.cpp":
g++ -o inCircle inCircle.cpp R2Graph.cpp

Студент должен сделать задачу, номер которой совпадает по модулю 2 с его номером по журналу (нечетные номера делают задачу 1, четные — задачу 2).
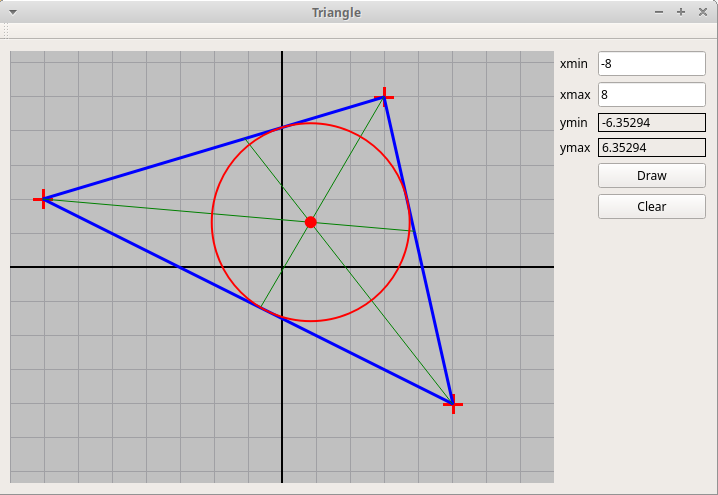
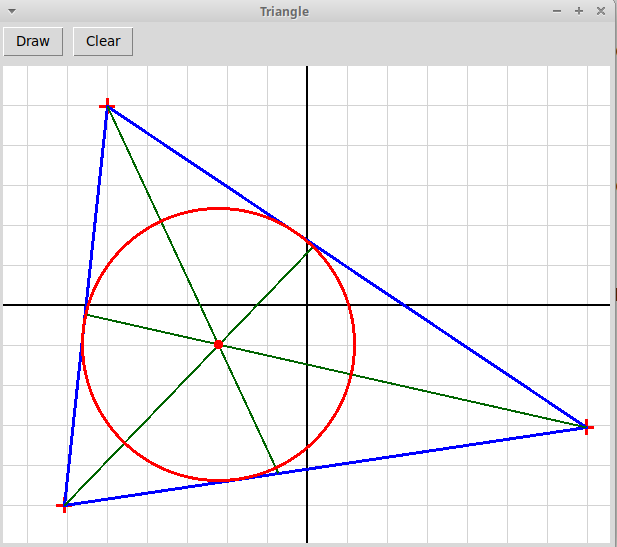
Задача должна быть реализована как графическая в среде Qt. В качестве образца можно использовать проект "Triangle.zip".
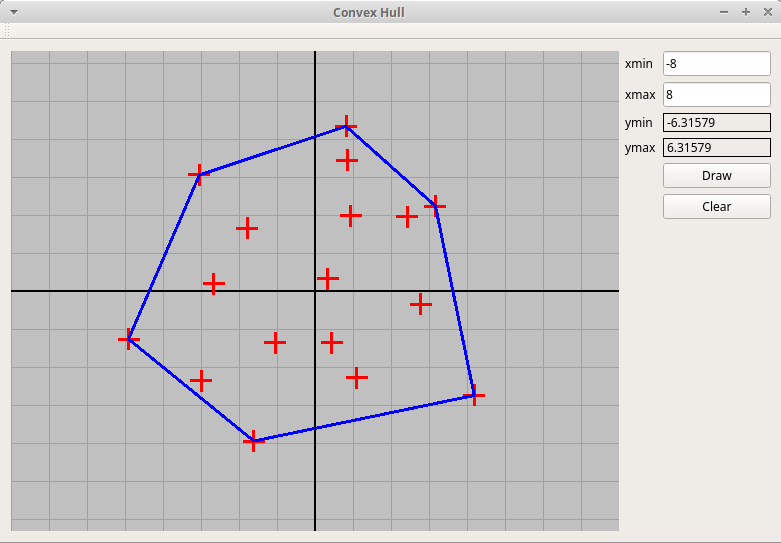
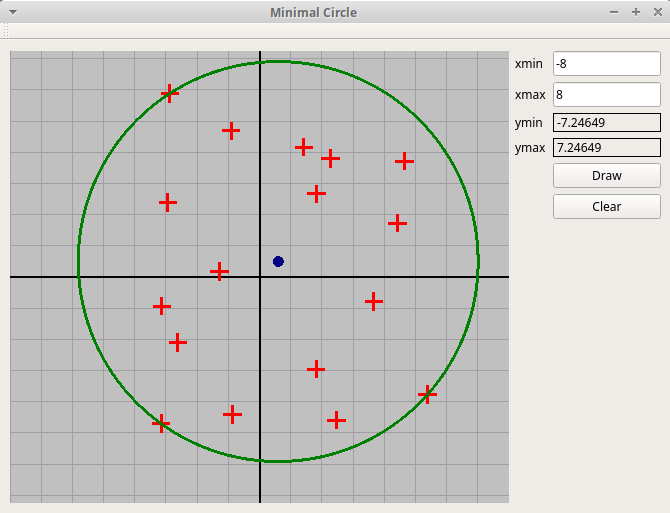
Для вычислений на плоскости R2 используются классы R2Vector (вектор на плоскости с вещественными координатами) и R2Point (точка на плоскости). В пакете "R2Graph.zip" реализованы все основные операции на плоскости.
Простой пример программы, использующей классы R2Point и R2Vector и потоковый ввод-вывод в стиле C++: ввести вершины треугольника и вычислить центр и радиус вписанной окружности. При вычислении запрещено использовать координаты векторов и точек, следует пользоваться исключительно методами классов R2Point и R2Vector. Файл "inCircle.cpp". Программа использует модуль R2Graph, в котором определяются классы для поддержки геометрии на плоскости: файлы "R2Graph.h" и "R2Graph.cpp". Архив всех файлов: InCircle.zip
Задачи:
написать консольное приложение, в котором вводятся 3 точки треугольника
и вычисляется
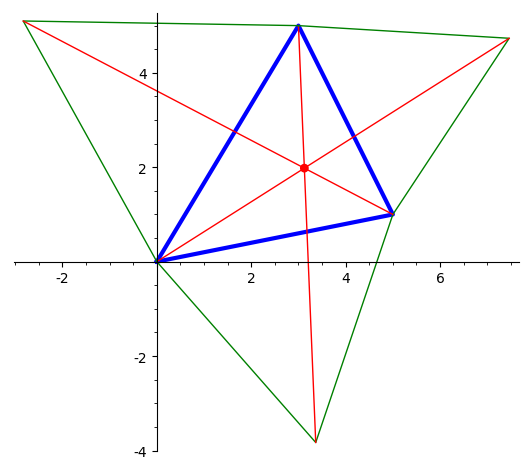
1) точка Нагеля треугольника

(пересечение отрезков, соединяющих вершины треугольника
с точками касания внешне-вписанных окружностей);
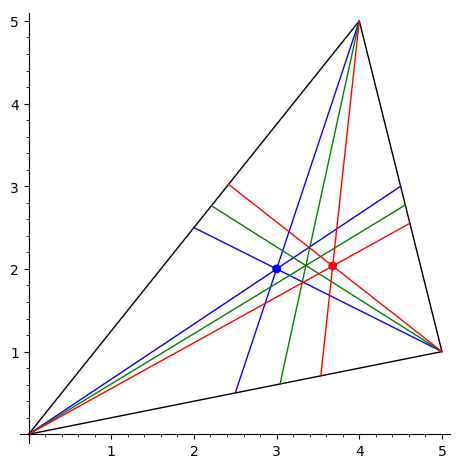
2) точка Лемуана треугольника

(пересечение симмедиан треугольника, т.е. линий,
симметричных медианам
относительно биссектрис; на рисунке медианы
изображены синим цветом, биссектрисы зеленым,
симмедианы красным).
Студенты с нечетными номерами по журналу делают первую задачу, с четными — вторую.
Мы используем классы R3Vector и R3Point, реализующие точки и векторы трехмерного пространства, для работы с картами земной поверхности. Координаты на поверхности Земли задаются широтой и долготой в градусах. Долгота точки — это угол между плоскостью гринвичского меридиана и плоскостью меридиана, проходящего через данную точку. Широта — это угол между радиус вектором, проведенным из центра Земли в данную точку, и плоскостью экватора. Эти углы измеряются в градусах. Долгота положительна для восточного полушария (и растет по мере продвижения на восток) и отрицательна в западном полушарии. Широта положительна в северном полушарии и отрицательна в южном.
Рассмотрим классическую задачу определения расстояния между двумя точками на поверхности Земли (приблизительно считаем поверхность Земли сферой). Самый простой способ ее решения — это найти угол между радиус-векторами, проведенными из центра Земли к этим точкам, и умножить его на радиус Земли. В классе R3Vector имеется метод angle, возвращающий угол между векторами, мы им воспользуемся. Все, что нам нужно — это реализовать функцию, определяющую радиус-вектор единичной длины, проведенный из центра Земли в направлении заданной точки.
Для представления векторов и точек на поверхности Земли мы используем
декартову систему координат, у которой начало координат расположено
в центре Земли.
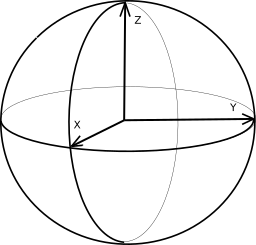 Ось x направлена из центра в точку перечесения
экватора и гринвичского меридиана, ось z направлена на северный
полюс, ось y перпендикулярна осям z и x и направлена
на восток.
Ось x направлена из центра в точку перечесения
экватора и гринвичского меридиана, ось z направлена на северный
полюс, ось y перпендикулярна осям z и x и направлена
на восток.
Радиус-вектор единичной длины, направленный из центра земли
в точку с широтой и долготой (lat, lon),
получается из базисного вектора
ex двумя поворотами: первый поворот на угол lat
выполняеся вокруг оси z, второй поворот на угол lon
выполняется в меридиональной плоскости.
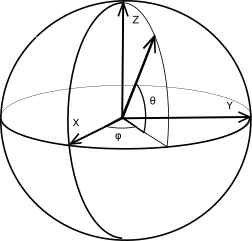 После первого поворота
мы получаем вектор
После первого поворота
мы получаем вектор
R3Vector radiusVector(double lat, double lon) {
double phi = lon*M_PI/180.; // Convert degrees to radians
double theta = lat*M_PI/180.;
// Rotate ex around ez by angle phi:
// v0 = (cos(phi), sin(phi), 0.)
// Then rotate v0 in meridional plane by angle theta:
// v1 = (cos(phi)*cos(theta), sin(phi)*cos(theta), sin(theta))
double cosTheta = cos(theta);
return R3Vector(
cos(phi)*cosTheta,
sin(phi)*cosTheta,
sin(theta)
);
}
(здесь используется константа M_PI = π, определенная в
заголовочном файле "math.h").
Полный текст программы: "earthdist.cpp". Проект использует также файлы "R3Graph.h" и "R3Graph.cpp", команда для компиляции проекта в Linux'е:
g++ -o earthdist earthdist.cpp R3Graph.cpp
Архив всех файлов:
"earthdist.zip".

|
Карта представляет собой касательную плоскость к земной сфере. Положение карты задается координатами ее центра: (широта центра, долгота центра). Для представления точек поверхности сферы на карте используется центральная проекция с центром в центре земного шара. На карте используется декартова система координат, в которой ось Y направлена на север (касательная к меридиану, проходящему через центр карты), ось X перпендикулярна оси Y и направлена на восток. Нужно решить одну из следующих двух задач (студенты с нечетными номерами решают 1-ю задачу, с четными — вторую). |
Задачи на замену
Нужно сделать одну задачу из трех, ее номер должен совпадать с номером студента по журналу по модулю 3.
void curcumSphere(
const R3Graph::R3Point tetrahedron[4],
R3Graph::R3Point& center,
double& radius
);
void inscribedSphere(
const R3Graph::R3Point tetrahedron[4],
R3Graph::R3Point& center,
double& radius
);
bool intersectTetrahedron(
const R3Graph::R3Point tetrahedron[4], // Тетраэдр
const R3Graph::R3Point& p, // Точка плоскости
const R3Graph::R3Point& normal, // Нормаль к плоскости
int& numVertices, // Число вершин многоугольника
R3Graph::R3Point intersection[4] // Многоугольник в пересечении
);
Функция должна возвращать true, если пересечение непусто,
и false в противном случае.
Пример 1: реализация класса Complex —
файлы "Complex.h",
"Complex.cpp", тестирующая программа
"complexTst.cpp",
"Makefile" для сборки проекта,
архив всех файлов "Complex.zip".
Пример 2: реализация класса Matrix (частичная) —
файлы "Matrix.h"
"Matrix.cpp", тестирующая программа
"MatrixTst.cpp",
"Makefile" для сборки проекта,
архив всех файлов "Matrix.zip".
Приведенная реализация класса Matrix намерено не доведена до конца, чтобы оставить возможность решения задач.
class Real {
. . .
Real(int intPart = 0, int fractionPart = 0);
Real(const char *string);
Real sqrt() const;
static Real fromString(const char *str);
char* toString(char* string, int maxLen) const;
. . .
};
В качестве тестовой программы написать программу решения
квадратного уравнения, корни находятся с точностью 0.001.
Архив файлов проекта: stdStackCalc.zip (файлы Stack.h, StackCalc.cpp).
Задача по проекту "Стековый калькулятор": добавить команды pi, e (математические константы), gcd (наибольший общий делитель), fastpow (быстрое возведение в целую неотрицательную степень), powmod (x^y (mod m) для целых чисел, y≥0, m>0).
Механизм шаблонов (template) в C++.
Контейнерные классы, реализующие популярные структуры данных
в стандартной библиотеке С++:
std::vector<Type>, std::deque<Type>,
std::set<KeyType>, std::map<KeyType, ValueType>.
Итераторы и их использование для реализации
цикла для каждого элемента x структуры данных выполнить
действие(x)
Программа "Телефонная книга", реализованная с помощью класса
std::map<std::string, std::string>
— файл "notebook.cpp".
Класс std::deque
Помимо стандартных контейнеров, в стандартной библиотеке STL языка C++ содержится также набор функций, реализующих типичные алгоритмы. Эти функции также являются шаблонами, т.е. зависят от параметров, заданных с помощью ключевого слова template. Это означает, что, например, функция сортировки sort может применяться для любых типов данных (базовых типов языка C/C++ или классов), поддерживающих сравнение элементов с помощью знака меньше "<".
Все стандартные алгоритмы описаны в заголовочном файле algorithm, который подключается с помощью строки
Отметим некоторые общие черты множества функций, содержащихся в стандартной библиотеке.
std::vector<int> a = { 10, 20, 77, 33, 45, 88, 99, 19 };
Чтобы упорядочить весь массив, надо вызвать функцию sort,
передав ей итераторы, указывающие на начало и за-конец массива:
std::sort(a.begin(), a.end());
Если же мы хотим упорядочить лишь отрезок массива, начинающийся
с элемента 77 и заканчивающийся элементом 88 включительно,
то нужно использовать следующую команду:
std::sort(a.begin() + 2, a.begin() + 6);
Здесь итератор a.begin()+2 указывает на элемент массива a с
индексом 2, т.е. на 77; итератор a.begin()+6 указывает на
элемент массива a с индексом 6, т.е. на 99 —
это элемент, непосредственно следующий за элементом 88, который
является последним элементом в сортируемом отрезке.
В первом случае мы просто сортируем массив b (копию начального массива a) по величине чисел:
std::vector<int> a = {
1, -10, 22, 36, -57, 102, 17, 19, 28, 15,
12, 18, -121, 343, -561
};
std::vector<int> b = a;
std::sort(b.begin(), b.end());
В втором случае мы сортируем массив b по абсолютной величине чисел, используя функцию сравнения cmp_abs:
b = a;
std::sort(b.begin(), b.end(), cmp_abs);
Функция cmp_abs определена следующим образом:
bool cmp_abs(int i0, int i1) {
return (abs(i0) < abs(i1));
}
В третьем случае сравнение двух целых чисел по их остаткам при делении на фиксированное число m выполняет объект класса CmpMod, число m=10 задается в конструкторе этого класса:
b = a;
std::sort(b.begin(), b.end(), CmpMod(10));
Класс CmpMod определен следующим образом:
class CmpMod {
int m;
public:
CmpMod(int mm = 5):
m(mm)
{}
bool operator()(int i0, int i1) const {
int r0 = i0 % m;
if (r0 < 0)
r0 += m;
int r1 = i1 % m;
if (r1 < 0)
r1 += m;
return (r0 < r1);
}
};
Вот результат работы программы:
Initial array: 1 -10 22 36 -57 102 17 19 28 15 12 18 -121 343 -561 ---- Sorted by value: -561 -121 -57 -10 1 12 15 17 18 19 22 28 36 102 343 ---- Sorted by absolute value: 1 -10 12 15 17 18 19 22 28 36 -57 102 -121 343 -561 ---- Sorted by residues modulo 10: -10 1 22 102 12 -57 343 15 36 17 28 18 19 -121 -561 ----
Программа нахождения множества слов в тексте на английском языке использующем кодировку ASCII: "words.cpp". Для каждого слова определяется количество его вхождений в текст. В результате печатается список слов, упорядоченных по количеству вхождений слов в текст, а для слов с одинаковым числом вхождений — лексикографически.
Программа "words.cpp". использует классы std::map, std::string, std::vector и алгоритм std::stable_sort.
Но рассмотренную выше программу "words.cpp" нельзя использовать для текстов на русском языке или любом другом языке, отличном от английского, поскольку стандартная библиотека STL языка С++ не поддерживает ни работу с UNICODE-символами, ни современную кодировку текстов в файлах UTF-8. Для работы с UNICODE и с UTF-8 мы используем самостоятельно написанный пакет функций utf8: "utf8.h", "utf8.cpp".
С использованием этого пакета, а также стандартных контейнерных классов и алгоритмов из библиотеки STL, реализована программа нахождения множества русских слов в тексте: "rusWords.cpp". Для каждого слова определяется количество его вхождений в текст. В результате печатается список слов, упорядоченных по количеству вхождений слов в текст, а для слов с одинаковым числом вхождений — лексикографически.
Программа "rusWords.cpp" использует классы std::map, std::basic_string, std::vector и алгоритм std::sort из стандартной библиотеки, а также функции для работы с Unicode-символами в кодировке UTF-8 — файлы "utf8.h", "utf8.cpp". Архив всех файлов проекта: "rusWords.zip".
Программа нахождения частот русских букв в тексте на русском языке: "ruschars.cpp", она также использует пакет функций "utf8". Архив всех файлов: "ruschars.zip".
Qt (Quazar Technology) — самая современная и самая лучшая среда для разработки C++ приложений. К достоинствам Qt относятся:
1) независимость текста программы от компьютера и операционной системы — исходные коды приложения одинаковы в Linux, MS Windows, Mac OS-X, и любых других современных операционных системах. В Qt можно создавать программы как для обычных компьютеров (Desktop), так и для операционных систем мобильных телефонов;
2) удобство программирования оконных и параллельных приложений благодаря удачному механизму сигналов и слотов;
3) поддержка огромного набора файловых форматов, сетевых протоколов и устройств;
4) программы на Qt, как правило, намного эффективнее, чем программы, подготовленные в других средах или на других языках, благодаря тому, что исполняющая система Qt автоматически учитывает особенности каждого конкретного компьютера и, к примеру, выбирает самый эффективный метод реализации графики (как правило, через трехмерный интерфейс, если в компьютере есть современная графическая карта);
5) Qt имеет очень удобную среду разработки qtcreator, которая позволяет редактировать оконные формы и добавлять обработчики сигналов, посылаемых управляющими элементами окон; qtcreator синхронно вносит изменения в h- и cpp-файлы.
Qt использует небольшое расширение базового языка C++ — добавлены ключевые слова signal, emit, slot, connect. Сигналы посылаются, например, управляющими элементами окон (для посылки сигнала используется ключевое слово emit). Слоты — это методы, предназначенныедля приема и обработки сигналов. С помощью вызова connect можно связать сигнал, посылаемый некоторым объектом, с обрабатывающим его слотом. При этом обработка выполняется не сразу путем вызова функции, а с помощью постановки сообщения о сигнале в очередь для последующей обработки объектом, принимающим этот сигнал. Такой способ гораздо более гибкий и безопасный, что важно при асинхронной обработке событий в многопоточных программах с параллельным исполнением нескольких нитей. Специальная утилита moc (Meta-Object Compiler) переводит программу с расширения языка С++ на чистый С++. Qt, в отличие от С++ варианта языка CLR-C++ (Сommon Language Runtime), являющегося частью платформы .Net фирмы Microsoft, не использует управляемую динамическую память и сборщик мусора. Благодаря этому Qt-программы быстрее, более надежны и тратят меньше памяти при выполнении, что позволяет использовать их в системах реального времени.
В Qt в основном разрабатываются оконные графические программы. Примеры несложных проектов:
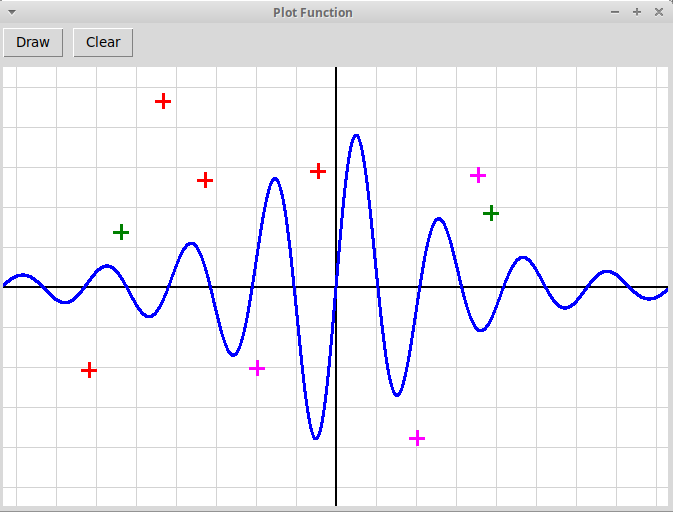
Qt-проект "График функции"
Изображается график функции, заданной непосредственно в тексте программы.
Также в точках, отмечаемых кликами мыши, рисуются крестики, цвета которых
задаются номером кнопки мыши (всего три цвета для трех кнопок):
PlotFunc.zip
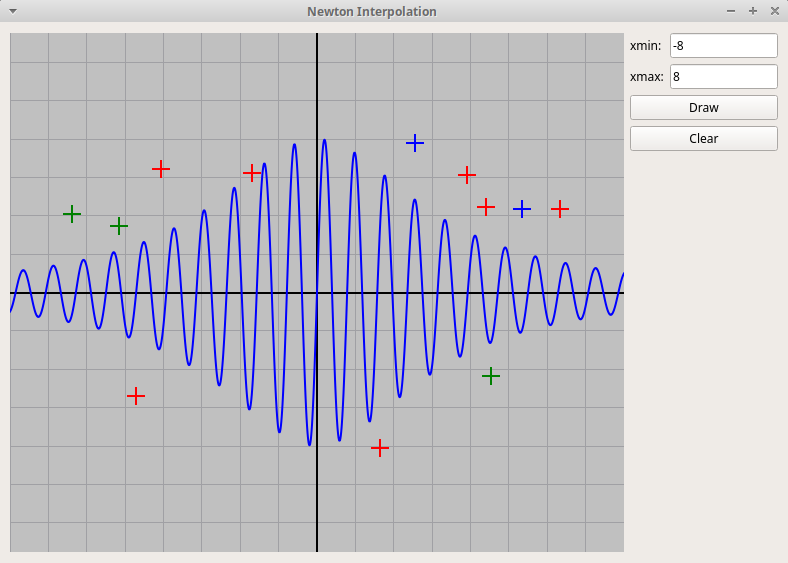
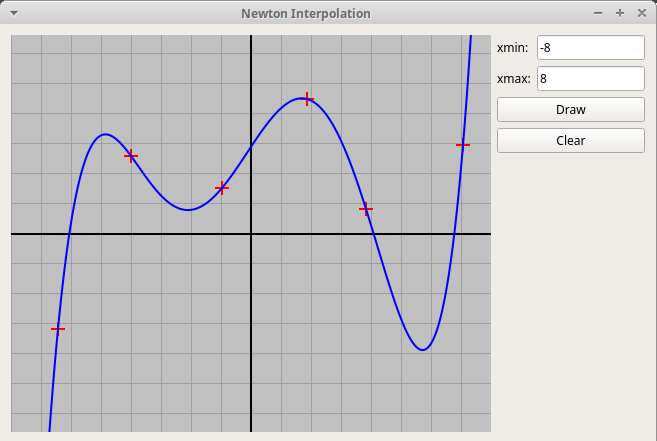
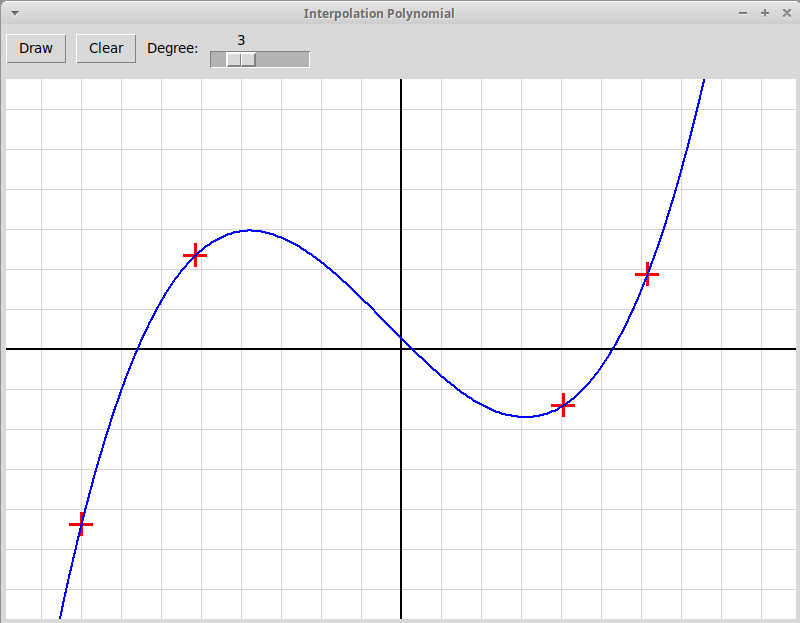
Qt-проект "График интерполяционного многочлена"
Пользователь кликами мыши задает узлы интерполяции,
которые отмечаются крестиками. По нажатию на клавишу "Draw"
программа рисует график интерполяционного многочлена, построенного
по этим узлам (вычисляется многочлен в форму Ньютона).
Узлы можно захватывать и перетаскивать мышью, при этом график многочлена
изменяется в реальном времени:
NewtonPol.zip

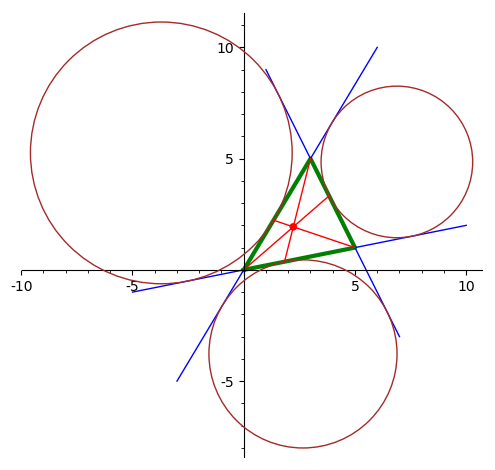
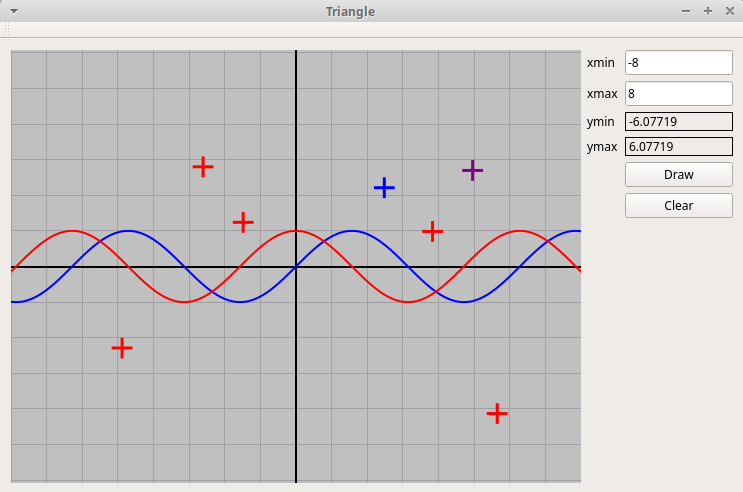
В задачах 2-5 надо нарисовать треугольник, задаваемый кликами мыши, и одну из замечательных точек треугольника, определяемых как пересечение чевиан. Нарисовать надо не только саму точку (в виде маленького закрашенного кружка), но и процесс ее построения. Нужно сделать одну задачу, номер которой совпадает по модулю 5 с номером студента по журналу.
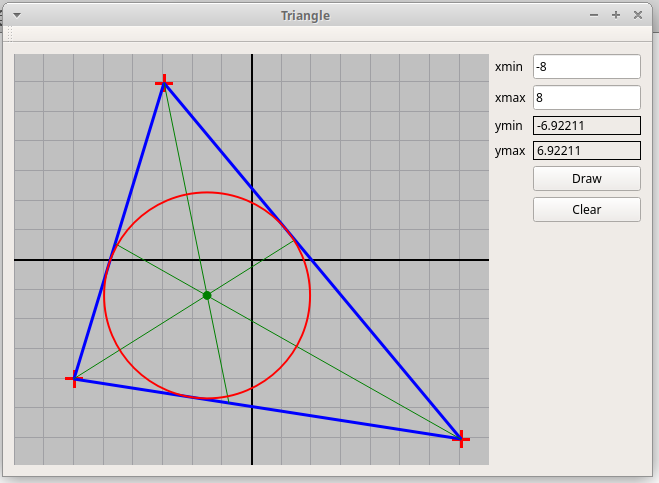
В качестве образца дается Qt-проект
"Triangle.zip",
в котором по трем кликам мыши изображается треугольник, его три
биссектрисы и вписанная окружность:
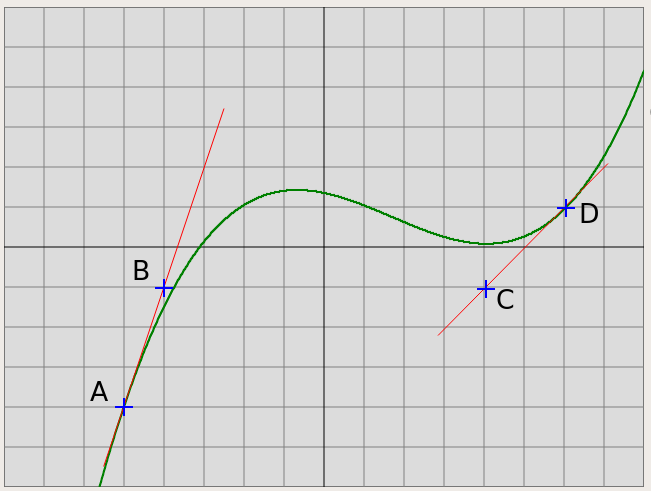
Указание: такой кубический многочлен удобно
вычислять в форме Ньютона. Обозначим
A.x=x0,
D.x=x1.
Нужно найти коэффициенты ai
в представлении многочлена
p(x) = a0 +
a1(x-x0) +
a2(x-x0)
(x-x1) +
a3(x-x0)2
(x-x1).




Тексты прочитанных лекций на "виртуальной доске"
(группа 202, весенний семестр 2021-22 учебного года).
Журнал группы химиков, 2 курс, 4 семестр 2022-23.
В задании 3 варианта, надо сделать ту задачу, номер которой совпадает по модулю 3 с номером студента по журналу.
Указание:
следует
1) найти список d всех собственных делителей числа m;
2) решить задачу о рюкзаке napsack(d, m).
Задача о рюкзаке
Имеется рюкзак объема m и список вещей, содержащий объемы
каждой вещи. Можно ли какими-то вещами из этого списка
(не обязательно всеми) заполнить рюкзак доверху?
d = [1, 2, 5, 3, 7, 11] m = 10
Можно ли из этого списка выбрать числа,
сумма которых равна 10?
2, 5, 3
3, 7
1, 2, 7
Эта задача NP-полная и для нее не существует хорошего
решения, кроме как полного перебора всех подмножеств.
Но, если не искать самого быстрого решения, то она легко
решается, например, применением рекурсии.
6, 3, 1, 2, 10, 4, 9, 12, 11, 8, 7, 5
2) для предшествующего к ней элемента x
(в примере x=9, выделен синим)
находим минимальный элемент y возрастающей последовательности,
больший x (в примере
y=11, отмечен подчеркиванием);
6, 3, 1, 2, 10, 4, 9, 12, 11, 8, 7, 5
3) меняем местами элементы x и y и затем упорядочиваем
элементы в конце перестановки, следующие за элементом y
(для этого используем метод sort для отрезка списка, следующего за y).
6, 3, 1, 2, 10, 4, 11, 5, 7, 8, 9, 12
Содержание лекции:
Презентация: теория чисел в криптографии
Файл numberth.py:
реализация базовых алгоритмов теории чисел на Python
d = u·m + v·n
Требуется решить одну задачу из списка. Номер задачи должен
совпадать с номером студента в журнале по модулю 4.
Решение должно быть оформлено в виде функции на языке Python3,
аргументами которой являются целые числа (одно или несколько).
Функция не должна содержать никаких операций ввода или вывода!
Ответ возвращается функцией в виде целого числа или логического
значения в зависимости от условия задачи. Пожалуйста,
присылайте мне решения (файл *.py, присоединенный к письму)
по электронной почте на адрес
vladibor2016 (собака) yandex.ru
primeTest(m)
должна возвращать True, если число m простое, и
False, если m составное. При этом вероятность ошибки
в случае ответа True не должна превышать $2^{-40} \approx 10^{-12}$
(т.е. должно пройти 20 случайных тестов). Заголовок функции:
def primeTest(m, k = 20):
где k — количество случайных тестов, 20 по умолчанию.
def pollardRho(m):
Функция должна раскладывать на множители не менее чем 20-значные
числа.
def pollardP1(m):
Функция должна раскладывать на множители не менее чем 20-значные
числа.
x ≡ ri (mod mi), i = 0, 1, ..., k-1.
Заголовок функции:
def chineseRemainderAlg(m, r):
Презентация: классы в Python'е
Прежде чем учиться писать свои собственные классы, давайте попробуем воспользоваться уже готовыми классами для решения задач. Рассмотрим геометрические задачи на плоскости R2, например, задачи на нахождение замечательных точек треугольника (центры вписанной и описанной окружностей, ортоцентр, точки Жергона, Нагеля, Лемуана, точка Ферма-Торричелли и т.п.). Все подобные задачи решаются легко и изящно, если использовать классы R2Vector и R2Point, реализующие вектор и точку на плоскости. Эти классы определены в модуле "R2Graph.py". Главная идея состоит в том, чтобы использовать методы этих классов вместо манипуляций с координатами векторов и точек, характерных для аналитической геометрии. Поскольку методы этих классов имеют ясный геометрический смысл, решение задач становится простым и геометрически наглядным, что значительно сокращает текст программы и уменьшает вероятность ошибок.
from R2Graph import *
u = R2Vector(1, 2)
v = R2Vector(3, -4)
С векторами возможны следующие операции:
>>> u + v
R2Vector(4.0, -2.0)
>>> u - v
R2Vector(-2.0, 6.0)
>>> u*0.75
R2Vector(0.75, 1.5)
>>> u*v
-5.0
>>> u = R2Vector(1, 2)
>>> u.norm()
2.23606797749979
>>> u.length()
2.23606797749979
>>> v
R2Vector(3.0, -4.0)
>>> n = v.normal()
>>> n
R2Vector(4.0, 3.0)
>>> u
R2Vector(1.0, 2.0)
>>> w = u.normalized()
>>> w
R2Vector(0.4472135954999579, 0.8944271909999159)
>>> u
R2Vector(1.0, 2.0)
>>> u.normalize()
R2Vector(0.4472135954999579, 0.8944271909999159)
>>> u
R2Vector(0.4472135954999579, 0.8944271909999159)
Класс R2Point реализует точку на плоскости. Разность двух точек является вектором, направленным от второй к первой точке:
>>> p1 = R2Point(1, 2)
>>> p2 = R2Point(3, -4)
>>> p1 - p2
R2Vector(-2.0, 6.0)
К точке можно прибавить или от нее отнять вектор, получим
точку, сдвинутую на указанный вектор:
>>> p1 + R2Vector(10, 20)
R2Point(11.0, 22.0)
Расстояние между точками p1 и p2 можно найти с помощью метода
distance:
>>> p1 = R2Point(0, 0)
>>> p2 = R2Point(1, 1)
>>> d = p1.distance(p2)
>>> d
1.4142135623730951
Расстояние от точки t до прямой, заданной точкой p и
направляющим вектором v, вычисляется с помощью метода
distanceToLine:
>>> t = R2Point(1, 1)
>>> p = R2Point(0, 1)
>>> v = R2Vector(1, -1)
>>> d = t.distanceToLine(p, v)
>>> d
0.7071067811865475
Наконец, в модуле
"R2Graph.py"
имеется функция intersectLines, вычисляющая точку пересечения
двух прямых. Каждая из прямых задается точкой и направляющим вектором.
Функция возвращает пару (intersected, q),
где intersected — логическое
значение, равное True, если прямые не параллельны, в этом случае
q — это точка пересечения прямых.
Если прямые параллельны,
то функция возвращает пару (False, None):
>>> p1 = R2Point(0, 2)
>>> v1 = R2Vector(1, 0)
>>> p2 = R2Point(0, 0)
>>> v2 = R2Vector(3, 1)
>>> intersectLines(p1, v1, p2, v2)
(True, R2Point(6.0, 2.0))
>>> intersectLines(p1, v1, p2, v1)
(False, None)
Презентация: классы в Python'е
1. Реализовать класс Треугольник на плоскости
class Triangle:
Методы:
-- конструктор (даются 3 точки в общем положении)
-- методы __str__ и __repr__, реализующие функции str(x) и
repr(x) для объекта x класса, возвращающие
текстовое представление объекта
-- __getitem__, __setitem__ (работа с треугольником как с массивом
из 3-х элементов)
-- периметр
-- площадь со знаком
-- площадь
-- ориентация (+1 если CCW, -1 CW)
-- centroid (центр тяжести)
-- точка внутри треугольника: True/False
-- ориентировать (если он отрицательно ориентирован, то изменить
порядок вершин)
-- вписанная окружность, возвращает пару (центр, радиус),
где центр имеет тип R2Point
-- описанная окружность, возвращает пару (центр, радиус)
Класс ДОЛЖЕН использовать модуль R2Graph, объект дожен хранить
вершины треугольника как список из трех элементов типа R2Point.
При реализации методов ЗАПРЕЩЕНО ПРОИЗВОДИТЬ ВЫЧИСЛЕНИЯ С КООРДИНАТАМИ
точек и векторов, все действия должны использовать только методы
классов R2Point и R2Vector (они имеют геометрическую интерпретацию).
2. Реализовать аффинное преобразование плоскости.
Transform
Любое аффинное преобразование есть композиция
линейного преобразования и сдвига
transform(p) = a*p + b
где a -- невырожденная матрица размера 2x2,
задающая линейное преобразование,
b -- вектор сдвига
-- конструктор, 2 варианта:
1) задается матрица a и R2Vector b;
2) задаются два треугольника t1 и t2, определяющие
аффинное преобразование: t1 --> t2
Каждый из треугольников задается как список из трех
элементов типа R2Point.
Например, можно создать объекты t1 и t2 типа Transform
следующими двумя способами:
t1 = Transform([[2., 1.], [-1., 2.]], R2Vector(3., 2.))
t2 = Transform(
[R2Point(-1, 0), R2Point(0, 0), R2Point(0, 1)],
[R2Point(0, 0), R2Point(5, 1), R2Point(3, 5)]
)
В первом случае мы указываем матрицу и вектор сдвига,
во втором случае -- два треугольника.
-- методы __str__ и __repr__, реализующие функции str(x) и
repr(x) для объекта x класса, возвращающие
текстовое представление объекта
-- произведение (композиция) преобразований
-- вычислить обратное преобразование
-- действие преобразования на точку
p2 = t*p1
где t -- аффинное преобразование, p1 -- исходная точка,
p2 -- ее образ под действием t.
Класс ДОЛЖЕН использовать модуль R2Graph.
3. Реализовать класс "вещественное число с фиксированной точкой",
FixedReal
которое представляется в виде
m*10^(-k),
m -- целое число (мантисса), k -- количество десятичных
цифр после десятичной точки.
Число k фиксировано, это статический член класса.
Например, если k = 3, то числа хранятся с точностью 3 знака
после десятичной точки
10.125 m = 10125 k = 3 (фиксировано)
3.500 == 3500
+ 0.720 == 720
--------------------
4.220 == 4220
3.500 * 0.720 == 3500*720//1000 = 2520
2.520
3.500 / 0.720 == 3500*1000//720 = 4861
4.861
Объект класса должен хранить внутри себя только целое число m, число k
является статическим членом класса, общим для всех объектов. Конструктор
должен по двум целым числам создавать объект: например, число x = 10.25 при
k = 3 создается как
x = FixedReal(10, 250)
Первый аргумент конструктора задает целую часть числа, второй -- дробную часть.
Поскольку точность k=3 знака после десятичной точки, число
10.25 можно записать как 10.250 и его дробная часть числа равна 250.
Число y = 1.03 создается как
y = FixedReal(1, 30)
(y = 1.030, дробная часть числа равна 30 тысячных).
Помимо конструктора, должны быть реализованы все арифметические операции,
а также методы __str__ и __repr__, представляющие функции str(x) и
repr(x) для объекта x, которые возвращают его текстовое представление.
Воспользовавшись этим классом, вычислить число e с точностью 1000 знаков
после десятичной точки (если не лень, то и 1000 знаков числа pi).
Матрица в Питоне обычно представляется списком строк, где каждая строка — это список чисел. Например,
>>> a = [[1, 2, 3], [4, 5, 6], [7, 8, 0]]
>>> print(a)
[[1, 2, 3], [4, 5, 6], [7, 8, 0]]
Замечательная особенность Питона состоит в том, что в нем реализованы целые числа неограниченного размера. Это позволяет реализовать также и рациональные числа. Реализация рациональных чисел с помощью целых чисел типа int или long long в языке C++ бессмысленна, т.к. при арифметических действиях с рациональными числами их знаменатели растут очень быстро и почти сразу наступает переполнение. В Питоне переполнений не бывает. Рациональные числа представлены в Питоне классом Fraction в модуле fractions:
>>> from fractions import *
>>> a = Fraction(1, 3)
>>> print(a)
1/3
>>> b = Fraction(1, 4)
>>> print(b)
1/4
>>> print(a + b)
7/12
Рациональные числа типа Fraction позволяют использовать точную арифметику и получать точный результат, в отличие от вещественных чисел типа float. Например, для типа float бессмыслено сравнивать числа на точное равенство, результат непредсказуем:
>>> a = 1/3
>>> a
0.3333333333333333
>>> b = 1/4
>>> b
0.25
>>> a + b
0.5833333333333333
>>> 7/12
0.5833333333333334
>>> 1/3 + 1/4 == 7/12
False
Неожиданный результат! Для вещественных чисел, представленных типом
float, сумма 1/3 + 1/4 не равна 7/12 (отличие мизерное,
но точного равенства нет).
Для матриц над полем рациональных чисел в Питоне можно реализовать метод Гаусса приведения матрицы к ступенчатому в точности так, как этот метод рассматривается в курсе математики. Это позволяет с помощью программ на Питоне решать задачи, которые обычно даются первокурсникам на практических занятиях в курсе алгебры или линейной алгебры: приведение матрицы к ступенчатому виду, вычисление определителя матрицы, решение систем линейных уравнений, вычисление обратной матрицы и т.п.
Отметим, что для матриц из вещественных чисел метод Гаусса имеет свои особенности: во-первых, мы не можем просто считать элемент равным нулю, поскольку точных равенств при работе с элементами типа float не бывает! Поэтому мы считаем элемент матрицы нулевым, если его абсолютная выличина не превосходит маленького числа eps, например, eps = 1e-8:
>>> (1/3 + 1/4) - 7/12 == 0
False
>>> eps = 1e-8
>>> abs((1/3 + 1/4) - 7/12) <= eps
True
Во-вторых, в методе Гаусса при приведении матрицы к ступенчатому
виду нельзя выбирать произвольный ненулевой разрешающий элемент в столбце.
Если мы выберем маленький ненулевой элемент, то при делении на него
строка в результате будет умножаться на очень большое число,
что приводит к экспоненциальному росту ошибок округления
и неустойчивости алгоритма.
В результате вместо правильного (или близкого к правильному)
ответа мы будем получать просто мусор! Надо обязательно выбирать элемент,
максимальный по абсолютной величине в столбце, чтобы при делении на него
строка умножалась на коэффициент, не превосходящий единицы.
В файле matrix.py реализована работа с матрицами на полем рациональных чисел (тип Fraction) и над полем вещественных чисел (тип float). Функция echelonFormOfRationalMatrix(a) приводит матрицу рациональных чисел к ступенчатому виду и возвращает пару (ступенчатый вид матрицы, ранг матрицы), при этом сама матрица a не изменяется (действия производятся с копией матрицы). Функция showRationalMatrix(a) преобразует объект "матрица" к текстовому виду так, чтобы потом матрицу можно было красиво напечатать:
>>> from matrix import *
>>> a = [[1, 2, 3], [4, 5, 6], [7, 8, 0]]
>>> print(showRationalMatrix(a))
[1 2 3]
[4 5 6]
[7 8 0]
>>> (b, rank) = echelonFormOfRationalMatrix(a)
>>> print(showRationalMatrix(b))
[ 1 2 3]
[ 0 -3 -6]
[ 0 0 -9]
Аналогичные функции echelonFormOfRealMatrix(a) и showRealMatrix(a) реализованы для вещественных матриц:
>>> a = [[1, 2, 3], [4, 5, 6], [7, 8, 0]]
>>> (b, rank) = echelonFormOfRealMatrix(a)
>>> print(showRealMatrix(b))
[ -7.0000 -8.0000 -0.0000]
[ -0.0000 -0.8571 -3.0000]
[ 0.0000 0.0000 4.5000]
Кроме того, в модуле matrix.py
реализованы функции вычисления определителя матрицы,
умножения матриц, а также выполнение элементарных преобразований
и копирование матриц.
В реальных приложениях, однако, никто не работает с матрицами большого размера как с базовыми списками Питона (матрица как список строк, каждая строка — список чисел). Связано это с тем, что такая работа с матрицами не очень эффективна. Для представления массивов и матриц (а также многомерных массивов) обычно используют модуль numpy и класс numpy.ndarray. Пример:
>>> import numpy as np
>>> a = np.array([[1., 2., 3.], [4., 5., 6.], [7., 8., 0.]])
>>> a
array([[1., 2., 3.],
[4., 5., 6.],
[7., 8., 0.]])
>>> type(a)
<class 'numpy.ndarray'>
>>> a.shape
(3, 3)
>>> a[0, 0]
1.0
>>> a[1][0]
4.0
>>> a[1]
array([4., 5., 6.])
>>> a[:,[1]]
array([[2.],
[5.],
[8.]])
В задании 2 варианта, нужно сделать одну задачу. Студенты с нечетными номерами по журналу делают задачу 1, с четными — задачу 2. В обеих задачах надо реализовать функцию, которая в зависимости от варианта возвращает либо матрицу, либо линейный массив. Реализованную функцию надо добавить в файл npmatrix.py.
В задачах предполагается, что матрицы и линейные массивы представляются numpy-массивами типа numpy.ndarray.
Отметим еще раз, что функция не должна ничего печатать (и уж тем более не должна ничего вводить с клавиатуры!). Результатом работы функции должно быть вычисление требуемого объекта, который функция должна возвращать с помощью оператора return. Исходные аргументы функции при этом меняться не должны.
b = inverseMatrix(a)
x = solveLinearSystem(a, b)
Здесь a — матрица вещественных чисел,
b — массив свободных членов уравнений.
Функция должна вернуть массив x вещественных чисел,
представляющий решение системыОтметим, что обе эти задачи реализованы в подмодуле linalg модуля numpy (linalg от слов линейные алгоритмы). Вычисление обратной матрицы к матрице a:
ainv = numpy.linalg.inv(a)
Решение системы линейных уравнений a·x = b:
x = numpy.linalg.solve(a, b)
Примеры:
>>> import numpy as np
>>> a = np.array([[1,2,3],[4,5,6],[7,8,0]], dtype="float64")
>>> ainv = np.linalg.inv(a)
>>> ainv
array([[-1.77777778, 0.88888889, -0.11111111],
[ 1.55555556, -0.77777778, 0.22222222],
[-0.11111111, 0.22222222, -0.11111111]])
>>> ainv @ a
array([[ 1.00000000e+00, -4.44089210e-16, 0.00000000e+00],
[ 2.22044605e-16, 1.00000000e+00, 0.00000000e+00],
[ 1.11022302e-16, 1.11022302e-16, 1.00000000e+00]])
>>> b = np.array([2., 3., 5.])
>>> x = np.linalg.solve(a, b)
>>> x
array([-1.44444444, 1.88888889, -0.11111111])
>>> a @ x
array([2., 3., 5.])
Однако пользоваться функциями из модуля numpy.linalg запрешено,
требуется самостоятельно реализовать функции вычисления обратной матрицы
и решения системы линейных уравнений.
Для графики мы используем модуль tkinter, представляющий собой наиболее простой оконный интерфейс. Мы также используем небольшой модуль R2Graph.py, в котором реализованы классы R2Vector и R2Point, с помощью которых удобно решать разные геометрические задачи на плоскости.
Подробный текст лекции: Графика на языке Python.




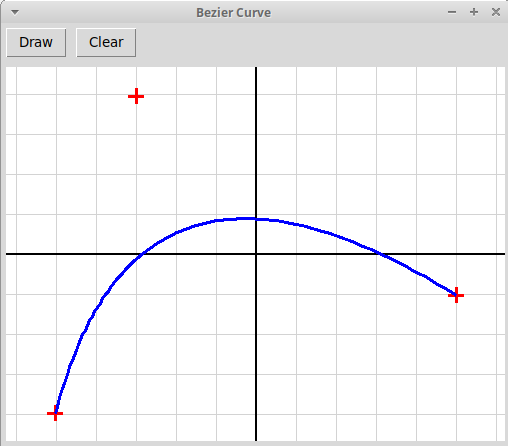
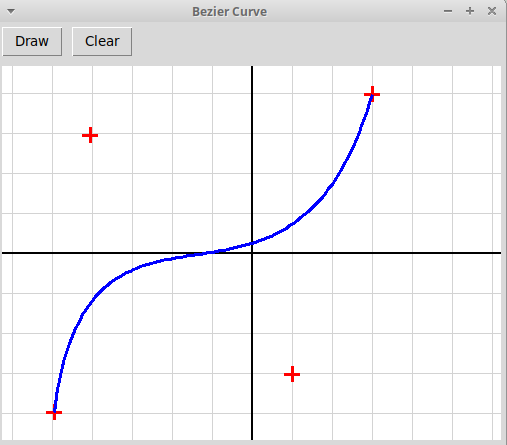
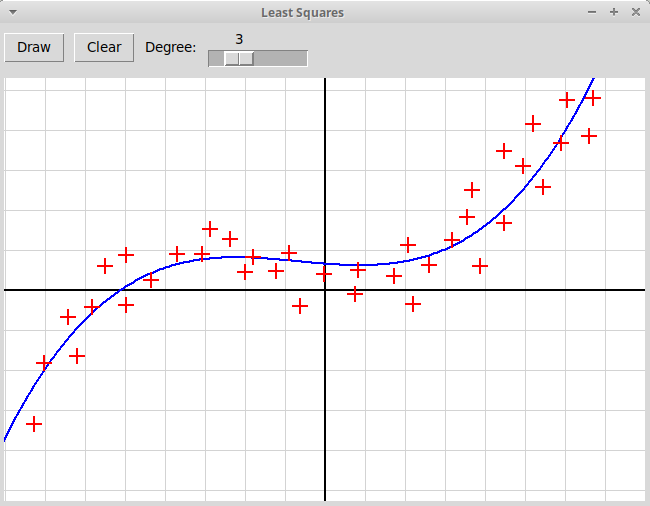
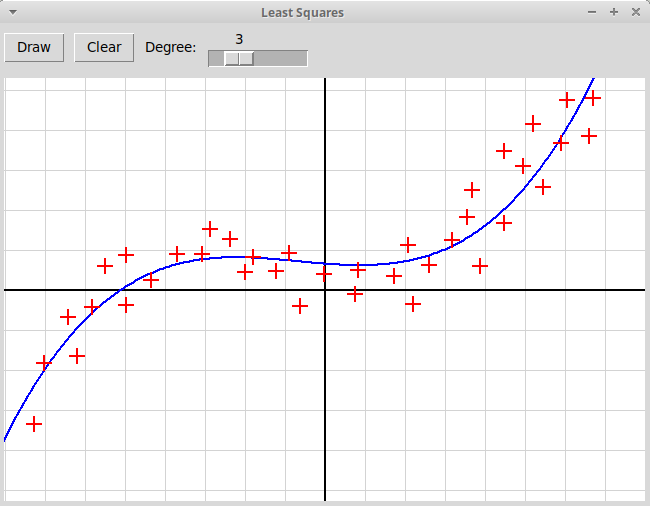
Написать, используя модуль tkinter, оконное графическое приложение,
иллюстрирующее метод наименьших квадратов.
Пользователь отмечает мышью набор точек на плоскости,
программа должна найти многочлен заданной степени,
минимизирующий сумму квадратов уклонений значений многочлена
от значений, заданных узлами интерполяции:
В качестве образца следует использовать
программу, рисующую график интерполяционного многочлена
по заданным узлам интерполяции; многочлен вычисляется по формуле
Ньютона:
Приложение использует два файла:
"newton.py" (оконный интерфейс),
"newtonPol.py" (вычисление полинома Ньютона).
Архив всех файлов:
"newtonInterpol.zip".
Замечание.
Вам файл "newtonPol.py"
не понадобится!
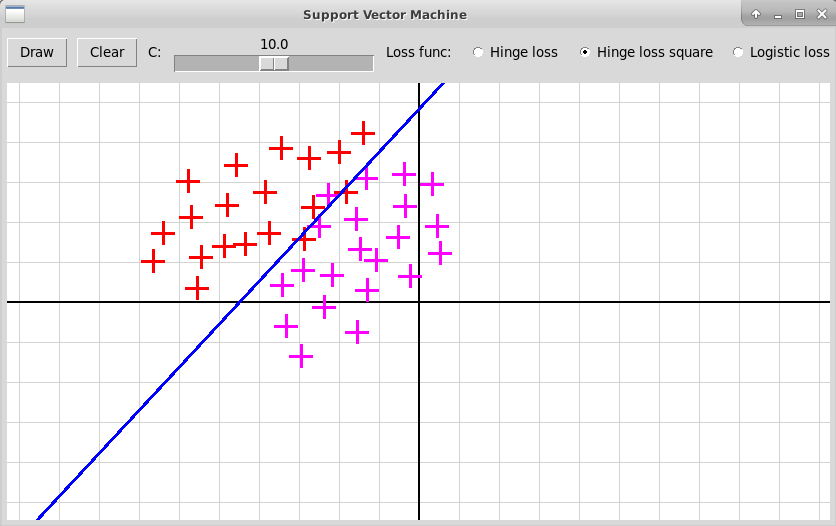
В классическом методе опорных векторов мы имеем два класса объектов, каждый объект описывается n признаками, представляемыми вещественными числами. Таким образом, объекты x1, x2, … xk представляются точками n-мерного пространства; координаты такой точки равны значениям признаков объекта. В тренировочной выборке объекты xi первого класса отмечены значением yi = 1, объекты xj второго класса — значением yj = -1. В методе опорных векторов SVM (Support Vector Machine) строится линейный классификатор f(x), который определяется как гиперплоскость, разделяющая два класса точек:
В классическом методе опорных векторов далеко не всегда можно разделить
гиперплоскостью два класса точек в n-мерном пространстве:
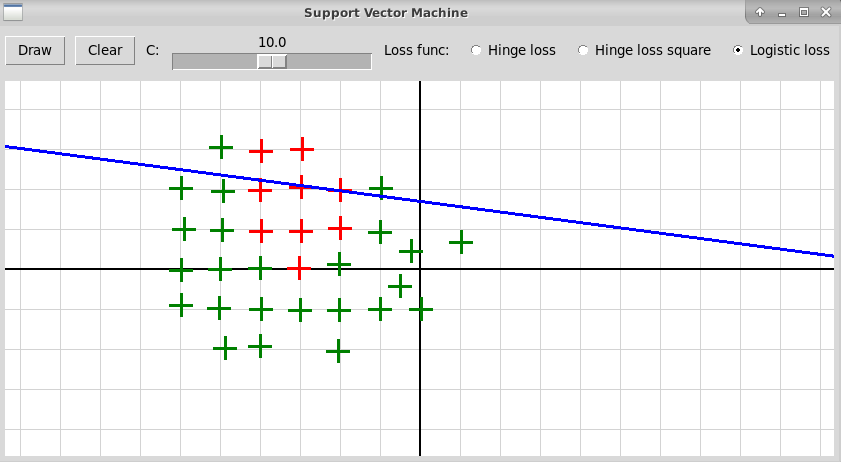
Идея нелинейного метода опорных векторов состоит в том, чтобы дополнить
исходный набор из n признаков объекта дополнительными признаками,
которые вычисляются как некоторые функции от набора исходных признаков.
В результате мы получим
множество точек в пространстве более высокой размерности, где каждая точка
представляет расширенный набор признаков исходного объекта. Можно надеяться,
что в пространстве более высокой размерности эти точки уже можно
разделить гиперплоскостью.
Итак, пусть отображение
В простейшем случае в качестве функций φ1(x1, … xn), φ2(x1, … xn), …, φm(x1, … xn) можно взять всевозможные мономы степени не выше d от переменных x1, x2, … xn (то есть от исходных признаков).
Пусть, например, d = 2. Пусть число исходных признаков n = 2, т.е. объекты представляются точками плоскости R2. Тогда расширенный набор признаков представляется всеми мономами степени не выше 2 от переменных x1, x2:
Программа "svmNonlinear.py" иллюстрирует использование нелинейного метода опорных векторов. Исходные объекты представляются точками плоскости двух цветов, отмечаемые кликами левой и правой клавиш мыши. В качестве расширенных признаков используются все мономы степени не выше d от координат x и y очередной точки; степень d задается с помощью слайдера в пределах от 1 до 5. Программа после построения нелинейного классификатора f(x) изображает линию нулевого уровня функции
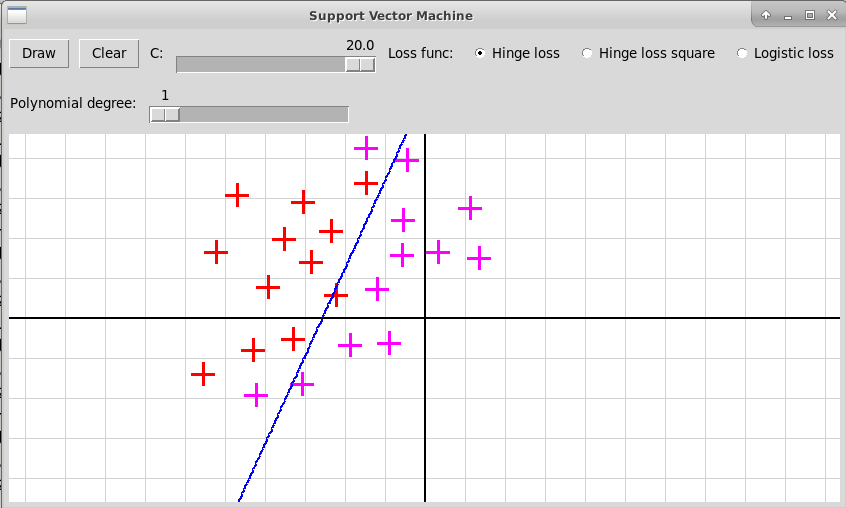
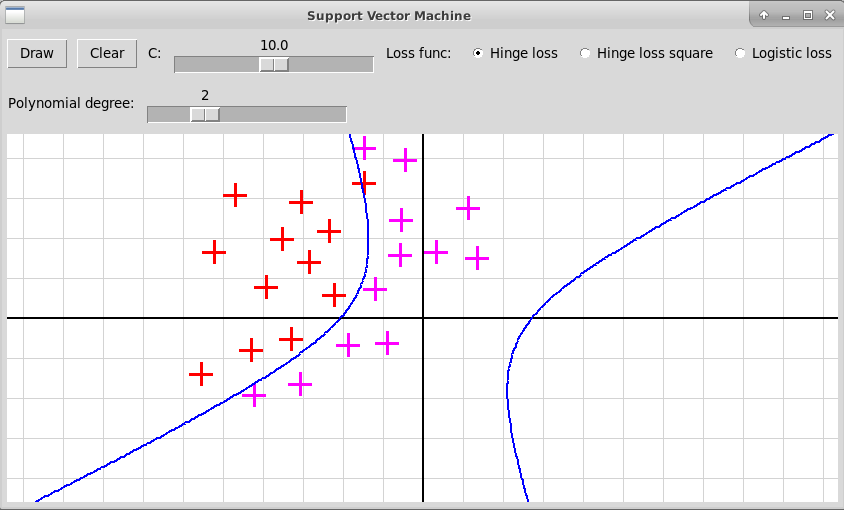
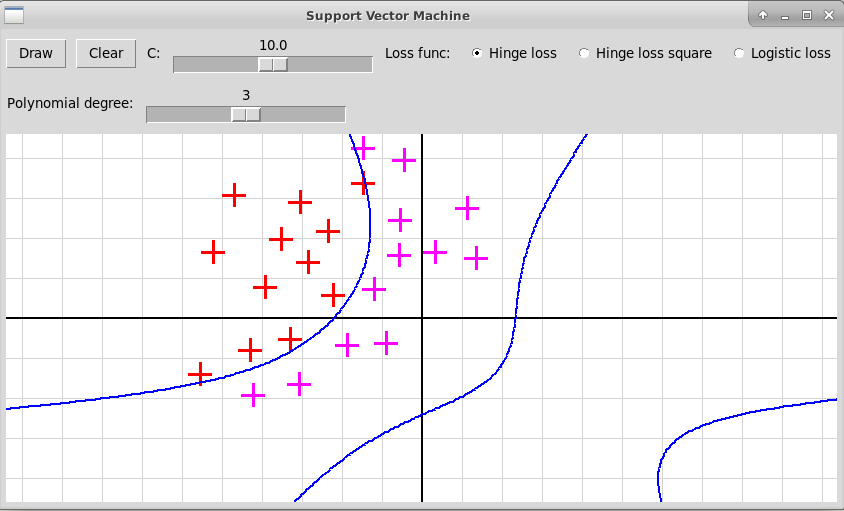
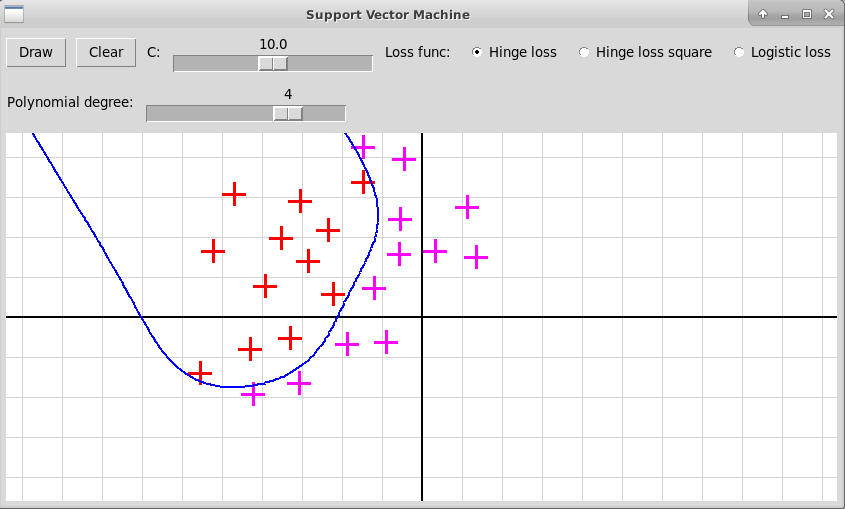
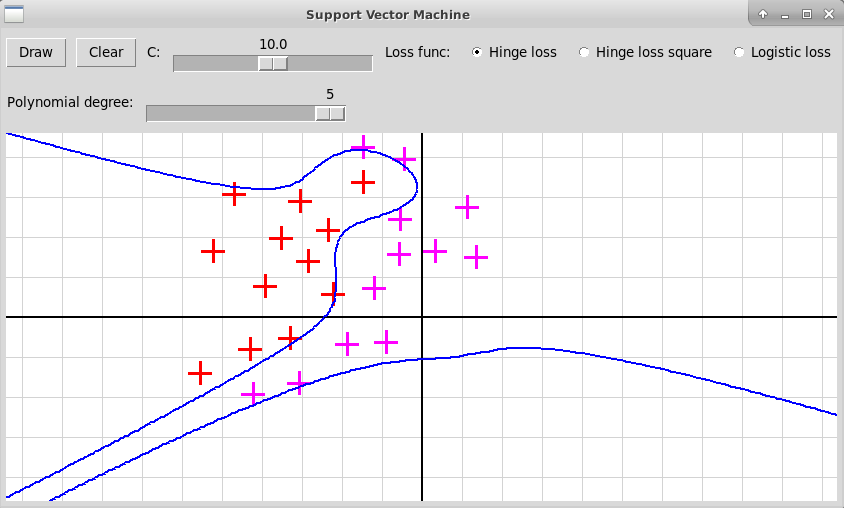
В случае полинома высокой степени 5 мы, скорее всего, наблюдаем переобучение. Также форма разделяющей кривой сильно заисит от гиперпараметра С и от функции потери.
Ниже приведен скрипт на Питоне в среде Jupyter-Lab, реализующий нелинейный метод опорных векторов. В программе генерируются два множества случайных точек, синие точки принадлежат первому классу, зеленые второму. Признаки объектов, т.е. две координаты точек, дополняются всеми мономами от координат степени не выше d. Разделяющая гиперплоскость, т.е. линейный классификатор
После построения классификатора программа рисует линию нулевого уровня
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize
import random
from math import sin, cos, pi
import itertools
from skimage import measure
plt.axes(aspect="equal")
xmin = -10; xmax = 14
ymin = -10; ymax = 14
plt.xlim(xmin, xmax)
plt.ylim(ymin, ymax)
plt.grid()
m = 100
m2 = m//2
v1 = np.array([2., 1.])
v1 /= np.linalg.norm(v1)
n1 = np.array([-v1[1], v1[0]])
class1 = [
v1*random.normalvariate(2., 2.) +
n1*random.normalvariate(0., 1.)
for i in range(m2)
]
plt.scatter(
[c1[0] for c1 in class1],
[c1[1] for c1 in class1],
color="blue"
)
class2 = []
ex = np.array([1., 0])
ey = np.array([0., 1.])
for i in range(m2):
phi = random.normalvariate(0., pi/2)
r = random.normalvariate(8., 1.)
p = ex*cos(phi)*r + ey*sin(phi)*r
class2.append([p[0], p[1]])
plt.scatter(
[c2[0] for c2 in class2],
[c2[1] for c2 in class2],
color="green"
)
classes = class1 + class2
x = np.array([[c[0], c[1]] for c in classes])
y = [1.]*m2 + [-1.]*m2
y = np.array(y)
# Shuffle training data
perm = np.random.permutation(m)
x = x[perm]
y = y[perm]
def monomials(x, degree=2):
res = [1.]
for d in range(1, degree + 1):
for p in itertools.combinations_with_replacement(x, d):
res.append(np.prod(p))
return res
C = 10. # Hyperparameter
degree = 3
xext = [ monomials(xx, degree) for xx in x ]
xext = np.array(xext)
k = len(xext[0])
wb0 = np.array([0.]*(k + 1))
wb0[0] = 1.
def hingeLoss(c):
return max(1. - c, 0.)
def lossFunction(wb):
w = wb[:-1]
b = wb[-1]
w2 = w @ w
s = 0.
for i in range(m):
c = y[i]*(w @ xext[i] - b)
s += hingeLoss(c)
return w2 + (C/m)*s
res = minimize(lossFunction, wb0)
# print(res)
wb = res.x
w = wb[:-1]
b = wb[-1]
print("w =", w)
print("b =", b)
def classifierFunction(x):
x_ext = monomials(x, degree)
return w @ x_ext - b
# Draw a line that separate two classes:
# This is the iso-line defined by the equation
# classifierFunction([x, y]) == 0.
rows = 50
cols = 50
dx = (xmax - xmin)/cols
dy = (ymax - ymin)/rows
def coordX(j):
return xmin + j*dx
def coordY(i):
return ymin + i*dy
a = [[0.]*cols for i in range(rows)]
a = np.array(a)
for i in range(rows):
yy = coordY(i)
for j in range(cols):
xx = coordX(j)
v = classifierFunction([xx, yy])
a[i, j] = v
# Draw the iso-line of zero level
contours = measure.find_contours(a, 0.)
for c in contours:
xx = []
yy = []
for p in c:
xx.append(coordX(p[1]))
yy.append(coordY(p[0]))
plt.plot(xx, yy, color="red")
# Uncomment for standalone application
# plt.show()
Результат работы программы:
Когда мы заменяем обычное скалярное произведение некоторым ядром, представляющим собой скалярное произведение векторов, составленных из набора базисных функций от исходных признаков, то в результате решения задачи минимизации функции потерь мы получаем нелинейный классификатор. При этом, несмотря на увеличение размерности пространства признаков, сложность вычислений остается такой же, как и в случае исходной линейной задачи.
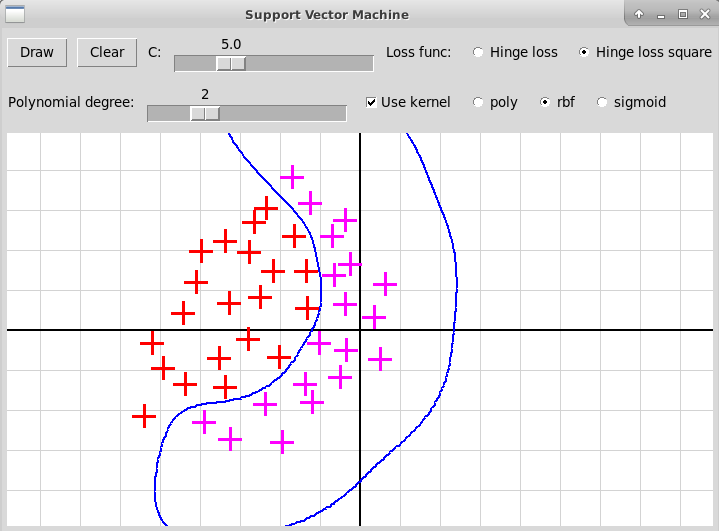
Вот несколько скриншотов оконной программы на Python+tkinter,
иллюстрирующей применение ядрового метода опорных векторов:
Гауссовское ядро (RBF)
Полиномиальное ядро, степень 2
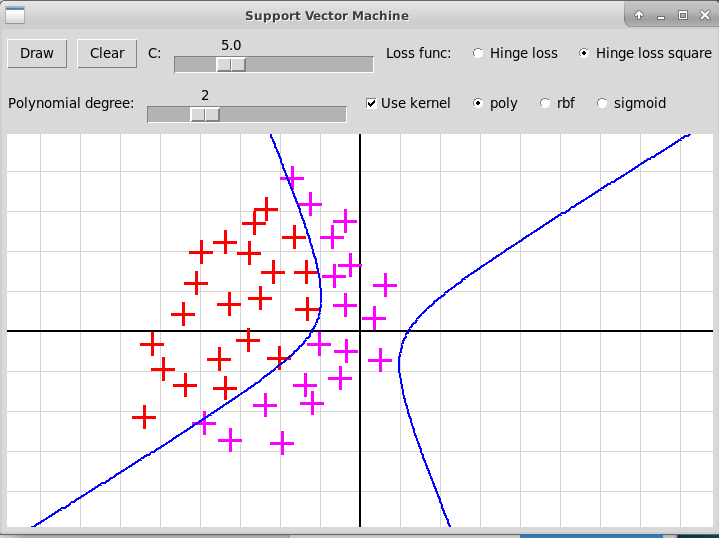
Полиномиальное ядро, степень 3
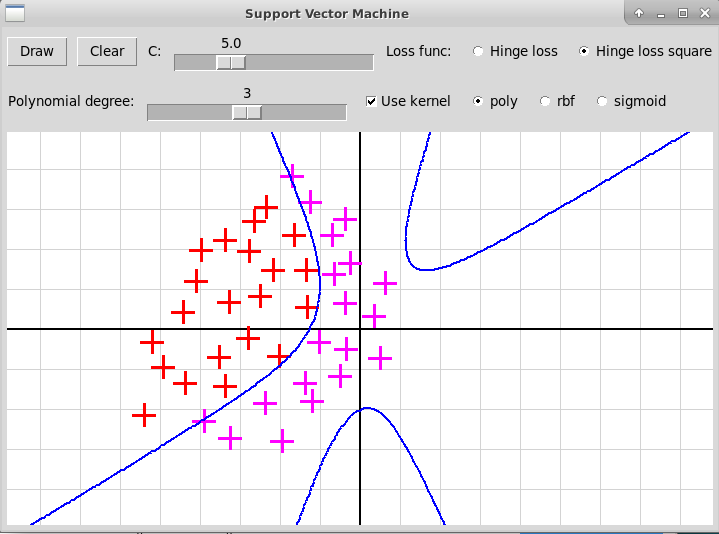
В этой программе используется модуль sklearn и его подмодуль svm, в котором реализован ядровый метод опорных векторов. В программе кликами мыши задается массив точек points, при этом точки, отмеченные кликом левой клавиши мыши, относятся к первому классу, другой клавишей — ко второму, номера клавиш мыши содержится в массиве mouseButtons. Вот как выглядит код, вызывающий метод опорных векторов.
Описания и глобальные переменные:
import numpy as np from sklearn.svm import SVC classifier = SVC(kernel="rbf")Обучение классификатора на тренировочной выборке:
global classifier
. . .
if kernel == "rbf":
classifier = SVC(C=c, kernel="rbf")
else:
classifier = SVC(C=c, kernel="poly", degree=polynomialDegree)
data = [
[points[i].x, points[i].y]
for i in range(len(points))
]
data = np.array(data)
y = [
(1. if mouseButtons[i] == 1 else (-1.))
for i in range(len(points))
]
y = np.array(y)
classifier.fit(data, y)
Для определения класса точки p
можно использовать два метода классификатора:
def classifierValue(p):
x = np.array([[p.x, p.y]])
# return classifier.predict(x)
return classifier.decision_function(x)
Используя значения, возвращаемые классификатором для точек плоскости, программа рисует линию нулевого уровня этой функции, заданную уравнением
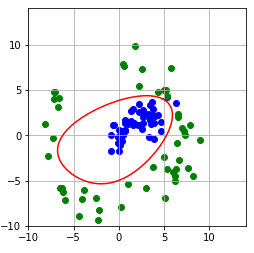
В среде Jupyter-Lab мы сначала генерируем на плоскости случайные точки двух классов так, чтобы их невозможно было разделить прямой линией. Затем мы применяем ядровый метод опорных векторов с Гауссовским ядром "rbf" (Radial Basis Function) и рисуем линию, которая разделяет два класса. Вот код программы (в среде Jupyter-Lab):
# Kernel Support Vector Machine
from scipy.optimize import minimize
import numpy as np
import random
from math import sin, cos
import matplotlib.pyplot as plt
from skimage import measure
from sklearn.svm import SVC
plt.axes(aspect="equal")
m1 = 100
class1 = [ np.array([
random.normalvariate(1., 1.5), random.normalvariate(1., 0.5)
]) for i in range(m1) ]
m2 = m1
angle1 = -np.pi*2/3
angle2 = np.pi*2/3
ex = np.array([1., 0.]); ey = np.array([0., 1.])
class2 = []
for i in range(m2):
phi = random.normalvariate(0., 1.)
r = random.normalvariate(5., 0.5)
p = ex*cos(phi)*r + ey*sin(phi)*r
class2.append(p.copy())
x = class1 + class2
x = np.array(x)
y = [1.]*len(class1) + [-1.]*len(class2)
y = np.array(y)
m = len(x)
perm = np.random.permutation(m)
x = x[perm]
y = y[perm]
plt.scatter(
[c[0] for c in x], [c[1] for c in x],
color=[ "r" if yy > 0. else "g" for yy in y ]
)
degree = 3
C = 2. # Hyperparameter
# classifier = SVC(C=C, kernel="poly", degree=degree)
classifier = SVC(C=C, kernel="rbf")
classifier.fit(x, y)
def classifierValue(x):
xx = np.array([ [x[0], x[1]] ])
# return classifier.predict(xx)
return classifier.decision_function(xx)
# Draw the separating line
xmin = min([xx[0] for xx in x]) - 1.
xmax = max([xx[0] for xx in x]) + 1.
ymin = min([xx[1] for xx in x]) - 1.
ymax = max([xx[1] for xx in x]) + 1.
steps = 100
def xcoord(j):
dx = (xmax - xmin)/steps
return xmin + j*dx
def ycoord(i):
dy = (ymax - ymin)/steps
return ymin + i*dy
# a is a matrix of dimension (steps, steps)
a = np.array([[0.]*steps for iy in range(steps)])
for i in range(steps):
for j in range(steps):
xx = np.array([xcoord(j), ycoord(i)])
a[i, j] = classifierValue(xx)
nullContours = measure.find_contours(a, 0.)
for c in nullContours:
plt.plot(
[xcoord(cc[1]) for cc in c],
[ycoord(cc[0]) for cc in c],
color="blue"
)
# Uncomment the following line for a standalone application
# plt.show()
Вот результат работы этой программы (запущенной в среде Jupyter-Lab):
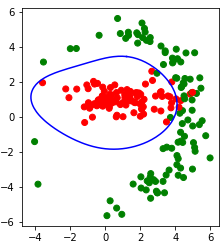
Исходный код программы:
"svmKernel.ipynb".
В этом году мы не успели пройти все темы по машинному обучению, поэтому в задании только один вариант.

from sklearn.svm import SVCПрограмма должна применить классификатор SVC и нарисовать линию, разделяющую точки двух классов. В программе должна быть реализована возможность выбора ядра из двух вариантов: "rbf" (Гауссовское ядро), "poly" (полиномиальное ядро). В случае полиномиального ядра степень полинома должна задаваться с помощью слайдера.